深度学习的优雅之处在于其优美的数学理论。反向传播算法不过是链式法则的一个巧妙应用,而梯度下降则是凸优化理论的直接推论。本文将从第一性原理出发,逐层深入这些数学基础,最后通过实际项目案例展示如何将理论应用于实践。
目录
- 深度学习中的数学体系
- 基础 0:核心数学基础速通
- 基础 1:深度学习算法与架构核心
- 第一部分:微积分基础
- 第二部分:链式法则与反向传播
- 第三部分:梯度下降与优化
- 第四部分:损失函数与信息论
- 第五部分:实际案例——从理论到代码
- 常见问题与深度洞察
深度学习中的数学体系
数学理论的层级结构
深度学习的数学基础可以分为四个层级:
1
2
3
4
5
6
7
8
9
┌─────────────────────────────────────┐
│ 应用层:神经网络架构设计 │
├─────────────────────────────────────┤
│ 算法层:优化方法(SGD、Adam等) │
├─────────────────────────────────────┤
│ 理论层:凸优化、泛函分析 │
├─────────────────────────────────────┤
│ 基础层:微积分、线性代数、概率论 │
└─────────────────────────────────────┘
这篇文章将重点关注基础层和理论层,这是所有高阶技巧的数学基础。
基础 0:核心数学基础速通
本节专为只想快速掌握核心概念的读者设计。如果你已经熟悉这些基础,可以直接跳到”第一部分”。
线性代数核心
1. 矩阵乘法——神经网络计算的基石
定义:矩阵 $A \in \mathbb{R}^{m \times n}$ 与矩阵 $B \in \mathbb{R}^{n \times p}$ 的乘积 $C = AB \in \mathbb{R}^{m \times p}$ 定义为:
\[C_{ij} = \sum_{k=1}^{n} A_{ik} B_{kj}\]神经网络中的意义:
- 输入向量 $\mathbf{x} \in \mathbb{R}^n$
- 权重矩阵 $\mathbf{W} \in \mathbb{R}^{m \times n}$
- 输出 $\mathbf{y} = \mathbf{W}\mathbf{x} + \mathbf{b}$ 就是矩阵乘法加偏置
计算复杂性:$O(mnp)$ — 这是为什么大模型这么慢的根本原因!
实际例子:
1
2
3
4
5
6
7
8
9
一个神经元层的计算:
输入:x ∈ ℝ^100 (100 个特征)
权重:W ∈ ℝ^64×100 (64 个神经元)
偏置:b ∈ ℝ^64
计算:y = W·x + b
结果:y ∈ ℝ^64 (64 个输出)
矩阵乘法运算数:64 × 100 = 6400 次乘法
2. 特征值与特征向量——理解矩阵的本质
定义:对于矩阵 $A \in \mathbb{R}^{n \times n}$,如果存在标量 $\lambda$ 和向量 $\mathbf{v} \neq \mathbf{0}$ 满足:
\[A\mathbf{v} = \lambda \mathbf{v}\]则 $\lambda$ 是 $A$ 的特征值,$\mathbf{v}$ 是对应的特征向量。
几何直观:矩阵作用在特征向量上,只是改变其大小(倍数为 $\lambda$),不改变方向。
在深度学习中的应用:
- Hessian 矩阵的特征值决定了二阶优化方法的收敛速度:
- 特征值都很小 → 收敛快
- 特征值差异大(条件数 $\kappa = \frac{\lambda_{\max}}{\lambda_{\min}}$ 大)→ 收敛慢
- 主成分分析(PCA)中:特征向量指向方差最大的方向
计算例子: \(A = \begin{pmatrix} 4 & 1 \\ 1 & 3 \end{pmatrix}\)
特征方程:$\det(A - \lambda I) = 0$ \((4-\lambda)(3-\lambda) - 1 = 0\) \(\lambda^2 - 7\lambda + 11 = 0\) \(\lambda_1 = \frac{7 + \sqrt{5}}{2} \approx 5.618, \quad \lambda_2 = \frac{7 - \sqrt{5}}{2} \approx 1.382\)
3. 矩阵转置——信息的反向流动
定义:矩阵 $A$ 的转置 $A^T$ 定义为 $(A^T){ij} = A{ji}$
关键性质: \((\mathbf{A}\mathbf{B})^T = \mathbf{B}^T\mathbf{A}^T\)
这在反向传播中至关重要!
在反向传播中的体现:
设正向传播为 $\mathbf{z} = \mathbf{W}\mathbf{x} + \mathbf{b}$,损失为 $L$。
则: \(\frac{\partial L}{\partial \mathbf{x}} = \frac{\partial L}{\partial \mathbf{z}} \frac{\partial \mathbf{z}}{\partial \mathbf{x}} = \mathbf{W}^T \frac{\partial L}{\partial \mathbf{z}}\)
注意梯度通过 $\mathbf{W}^T$ 反向传播!
4. 矩阵的秩——数据维度的真相
定义:矩阵的秩 $\text{rank}(A)$ 是其行向量(或列向量)的最大线性无关个数。
关键性质:
- 对于 $A \in \mathbb{R}^{m \times n}$:$\text{rank}(A) \leq \min(m, n)$
- 如果 $\text{rank}(A) = \min(m, n)$,则称矩阵满秩(full rank)
- 满秩矩阵可逆
在深度学习中的意义:
- 避免秩亏:如果权重矩阵秩太低,信息会丢失
1 2 3 4 5 6
秩为 1 的权重矩阵: W = u·v^T (外积) 这意味着输出在一维子空间中, 无论输入如何,都在这个方向上。 这非常限制了模型的表达能力。
-
奇异值分解(SVD):$A = U\Sigma V^T$,秩等于 $\Sigma$ 中非零元素个数
- 过参数化理论:深层网络的权重矩阵通常秩较低,这是一个有趣的现象!
实例:
1
2
3
4
5
矩阵 A = [1 2] 秩 = 1
[2 4] (第二行是第一行的 2 倍)
矩阵 B = [1 0] 秩 = 2
[0 1] (满秩,可逆)
小结:矩阵运算的内存/计算复杂性
| 操作 | 复杂性 | 备注 |
|---|---|---|
| 矩阵乘法 $A_{m×n} \times B_{n×p}$ | $O(mnp)$ | 瓶颈操作,GPU 优化 |
| 矩阵转置 | $O(mn)$ | 内存也是 $O(mn)$ |
| 特征值分解 | $O(n^3)$ | 计算代价大,很少用于大规模网络 |
| 求逆 | $O(n^3)$ | 数值不稳定,通常用求解而非求逆 |
微积分核心
1. 导数与偏导数——变化率的度量
单变量导数: \(f'(x_0) = \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h}\)
几何意义:曲线在该点的切线斜率。
多变量偏导数:对于 $f(x_1, x_2, \ldots, x_n)$:
\[\frac{\partial f}{\partial x_i} = \lim_{h \to 0} \frac{f(x_1, \ldots, x_i+h, \ldots, x_n) - f(x_1, \ldots, x_n)}{h}\]关键性质:混合偏导数相等(连续函数) \(\frac{\partial^2 f}{\partial x_i \partial x_j} = \frac{\partial^2 f}{\partial x_j \partial x_i}\)
2. 梯度——最陡峭的攀登方向
定义:梯度是所有偏导数的列向量:
\[\nabla f = \begin{pmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots \\ \frac{\partial f}{\partial x_n} \end{pmatrix}\]最重要的性质:
- 方向:指向函数增长最快的方向
- 大小:$|\nabla f|$ 表示增长速率
- 方向导数:在方向 $\mathbf{u}$ 上的导数 = $\nabla f \cdot \mathbf{u}$
在神经网络中:
1
2
3
4
5
6
神经网络损失函数 L(θ₁, θ₂, ..., θ_M)
其中 M 可能是数百万个参数
梯度 ∇L 就是这数百万个偏导数的向量
梯度下降:θ_{t+1} = θ_t - α·∇L(θ_t)
3. 链式法则——反向传播的数学本质
一维情况:如果 $y = f(g(x))$,则: \(\frac{dy}{dx} = \frac{dy}{dg} \cdot \frac{dg}{dx}\)
多维情况:对于 $y = f(\mathbf{g}(\mathbf{x}))$,其中:
- $\mathbf{x} \in \mathbb{R}^n$
- $\mathbf{g}: \mathbb{R}^n \to \mathbb{R}^m$
- $f: \mathbb{R}^m \to \mathbb{R}$
梯度关系(矩阵形式): \(\nabla_{\mathbf{x}} f = J_{\mathbf{g}}^T \nabla_{\mathbf{g}} f\)
其中 $J_{\mathbf{g}}$ 是 $\mathbf{g}$ 的 Jacobian 矩阵:
\[J = \begin{pmatrix} \frac{\partial g_1}{\partial x_1} & \cdots & \frac{\partial g_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial g_m}{\partial x_1} & \cdots & \frac{\partial g_m}{\partial x_n} \end{pmatrix}\]为什么链式法则是反向传播?
神经网络是函数复合:$y = f_L(f_{L-1}(\cdots f_1(\mathbf{x})))$
应用链式法则: \(\frac{\partial L}{\partial \mathbf{x}} = \frac{\partial L}{\partial f_L} \cdot \frac{\partial f_L}{\partial f_{L-1}} \cdot \ldots \cdot \frac{\partial f_1}{\partial \mathbf{x}}\)
这正是反向传播:从输出层逐层向输入层传播梯度!
4. 方向导数与梯度的关系
方向导数(沿单位向量 $\mathbf{u}$ 的方向): \(D_{\mathbf{u}} f = \nabla f \cdot \mathbf{u} = \|\nabla f\| \cos\theta\)
其中 $\theta$ 是梯度与方向的夹角。
三个关键角度:
- $\theta = 0°$:沿梯度方向,$D_{\mathbf{u}}f = |\nabla f|$(最快增长)
- $\theta = 90°$:垂直于梯度,$D_{\mathbf{u}}f = 0$(函数值不变)
- $\theta = 180°$:逆梯度方向,$D_{\mathbf{u}}f = -|\nabla f|$(最快下降)
这正是梯度下降的理论基础!
概率统计核心
1. 正态分布——深度学习中的主角
概率密度函数(PDF): \(f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\)
记号:$x \sim \mathcal{N}(\mu, \sigma^2)$
参数意义:
- $\mu$:均值(中心位置)
- $\sigma^2$:方差(离散程度)
- $\sigma$:标准差
标准正态分布:$\mu = 0, \sigma = 1$,记为 $Z \sim \mathcal{N}(0,1)$
多元正态分布:$\mathbf{x} \in \mathbb{R}^n$ 满足:
\[f(\mathbf{x}) = \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}} \exp\left(-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^T\Sigma^{-1}(\mathbf{x}-\boldsymbol{\mu})\right)\]其中 $\Sigma$ 是协方差矩阵。
在深度学习中的应用:
- 权重初始化(He 初始化、Xavier 初始化):从正态分布采样
1 2 3 4 5
# He 初始化(针对 ReLU) W ~ N(0, 2/n_in) # 这个方差的选择基于统计分析 # 确保梯度在网络传播时不会爆炸或消失
-
批量归一化(Batch Normalization):将激活值归一化为接近标准正态
- Dropout 正则化:随机丢弃神经元,等价于集成多个模型
2. 期望与方差——数据特征的量化
期望(均值): \(\mathbb{E}[X] = \int_{-\infty}^{\infty} x f(x) dx\)
方差: \(\text{Var}(X) = \mathbb{E}[(X - \mathbb{E}[X])^2] = \mathbb{E}[X^2] - (\mathbb{E}[X])^2\)
标准差:$\sigma = \sqrt{\text{Var}(X)}$
协方差(两个变量的相关性): \(\text{Cov}(X, Y) = \mathbb{E}[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])]\)
相关系数(无量纲的协方差): \(\rho = \frac{\text{Cov}(X,Y)}{\sigma_X \sigma_Y} \in [-1, 1]\)
在神经网络中的意义:
1
2
3
4
5
6
7
8
9
10
11
12
13
假设某层的激活值 z ~ N(μ, σ²)
- 如果 σ 很大:激活值极端分散
→ Sigmoid 饱和(梯度接近 0)
→ 学习缓慢
- 如果 σ 很小:激活值聚集
→ 很多信息丢失
→ 网络表达能力受限
- 最优情况:σ ≈ 1(标准化)
→ 梯度流动最优
→ 学习最快
3. 概率分布的KL散度——衡量分布差异
KL 散度(相对熵):
\[D_{KL}(P \| Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}\]对连续分布: \(D_{KL}(P \| Q) = \int P(x) \log \frac{P(x)}{Q(x)} dx\)
关键性质:
- $D_{KL}(P | Q) \geq 0$,等号成立当且仅当 $P = Q$
- 不对称性:$D_{KL}(P | Q) \neq D_{KL}(Q | P)$
推导交叉熵:
\(D_{KL}(P \| Q) = \sum_x P(x)[\log P(x) - \log Q(x)]\) \(= -H(P) + H(P,Q)\)
其中:
- $H(P) = -\sum_x P(x) \log P(x)$ 是 $P$ 的熵(常数,真实分布固定)
- $H(P,Q) = -\sum_x P(x) \log Q(x)$ 是交叉熵(可优化)
因此:最小化 KL 散度 = 最小化交叉熵
4. 贝叶斯定理——从先验到后验
贝叶斯定理: \(P(A|B) = \frac{P(B|A)P(A)}{P(B)}\)
术语:
- $P(A)$:先验(先前的信念)
-
$P(B A)$:似然(观测到数据的可能性) -
$P(A B)$:后验(更新后的信念) - $P(B)$:证据(常数,归一化因子)
在机器学习中的应用:
设 $\theta$ 是模型参数,$D$ 是观测数据:
\[P(\theta|D) = \frac{P(D|\theta)P(\theta)}{P(D)}\]最大后验估计(MAP): \(\theta^* = \arg\max_\theta P(\theta|D) = \arg\max_\theta P(D|\theta)P(\theta)\)
贝叶斯解释 L2 正则化:
假设参数先验:$P(\theta) = \mathcal{N}(0, \sigma^2)$
1
2
-log P(θ|D) = -log P(D|θ) - log P(θ) + const
∝ L(θ) + λ||θ||₂²
因此,L2 正则化等价于高斯先验!参数 $\lambda$ 反映了我们对参数大小的先验信念。
5. 大数定律与中心极限定理
大数定律:设 $X_1, X_2, \ldots$ 独立同分布,$\mathbb{E}[X_i] = \mu$,则:
\[\frac{1}{n}\sum_{i=1}^n X_i \xrightarrow{p} \mu \quad \text{当 } n \to \infty\]在 SGD 中的应用:小批量的平均梯度趋向于全批量梯度
中心极限定理(CLT):样本均值的分布趋向于正态分布
\[\bar{X}_n = \frac{1}{n}\sum_{i=1}^n X_i \xrightarrow{d} \mathcal{N}\left(\mu, \frac{\sigma^2}{n}\right)\]在深度学习中的含义:
- 即使原始数据分布不正态,激活值的分布也会趋向正态(在深层网络中)
- 这解释了为什么批量归一化会假设数据近似正态分布
- 这也是为什么权重初始化时使用正态分布是合理的
核心概念速查表
| 概念 | 定义 | 在神经网络中的作用 |
|---|---|---|
| 矩阵乘法 | $C_{ij} = \sum_k A_{ik}B_{kj}$ | 前向传播的基本计算 |
| 特征值 | $A\mathbf{v} = \lambda\mathbf{v}$ | 优化速度(条件数) |
| 秩 | 线性无关行/列的个数 | 数据维度和表达能力 |
| 转置 | $(A^T){ij} = A{ji}$ | 反向传播时梯度流向 |
| 梯度 | $\nabla f = [\partial_1 f, \ldots, \partial_n f]^T$ | 优化的方向和速度 |
| 链式法则 | $\frac{dy}{dx} = \frac{dy}{dz}\frac{dz}{dx}$ | 反向传播的数学本质 |
| 正态分布 | $f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$ | 权重初始化、数据假设 |
| 方差 | $\text{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2$ | 数据标准化 |
| KL 散度 | $D_{KL}(P|Q) = \sum P(x)\log\frac{P(x)}{Q(x)}$ | 交叉熵损失函数 |
| 贝叶斯定理 | $P(A|B) = \frac{P(B|A)P(A)}{P(B)}$ | L2 正则化的解释 |
基础 1:深度学习算法与架构核心
本节从算法和架构的角度,讲解深度学习的核心构件。这是从”纯数学”到”可工作的模型”的桥梁。
感知机与多层感知机
1. 单层感知机(Perceptron)——第一个神经网络
历史背景:感知机是 Rosenblatt 在 1958 年提出的,是现代神经网络的祖先。
模型定义:
给定输入 $\mathbf{x} \in \mathbb{R}^n$ 和权重 $\mathbf{w} \in \mathbb{R}^n$、偏置 $b \in \mathbb{R}$:
\[z = \mathbf{w} \cdot \mathbf{x} + b = \sum_{i=1}^n w_i x_i + b\] \[\hat{y} = \text{sign}(z) = \begin{cases} 1 & \text{if } z > 0 \\ -1 & \text{otherwise} \end{cases}\]其中 $\text{sign}$ 是阶跃函数。
几何直观:感知机学到的是一条分割线(或高维的超平面)。
1
2
3
4
5
6
7
对于 2D 二分类问题:
Class 1 •••
•••
————————————— 决策边界(由 w·x + b = 0 定义)
•••
Class -1•••
学习算法(感知机规则):
1
2
3
4
5
6
7
8
初始化:w ← 0, b ← 0
重复直到收敛:
对每个样本 (x_i, y_i):
z = w·x_i + b
ŷ = sign(z)
如果 ŷ ≠ y_i: # 预测错误
w ← w + y_i · x_i
b ← b + y_i
为什么有效:每当预测错误时,我们朝着正确标签的方向调整权重。
关键限制:
- ❌ 只能解决线性可分问题
- ❌ XOR 问题无法解决(经典的反例)
1
2
3
4
5
6
7
8
9
XOR 问题:
输入 | 输出
-----+----
0, 0 | 0
0, 1 | 1
1, 0 | 1
1, 1 | 0
不存在一条直线能分离这些点!
2. 多层感知机(MLP)——深度学习的基础
突破点:添加隐藏层和非线性激活函数!
架构:
1
2
3
4
5
输入层 x 隐藏层 h 输出层 ŷ
x₁ h₁
x₂ ────(W₁,b₁)── h₂ ───(W₂,b₂)── ŷ
x₃ h₃
(n维) (m维) (k维)
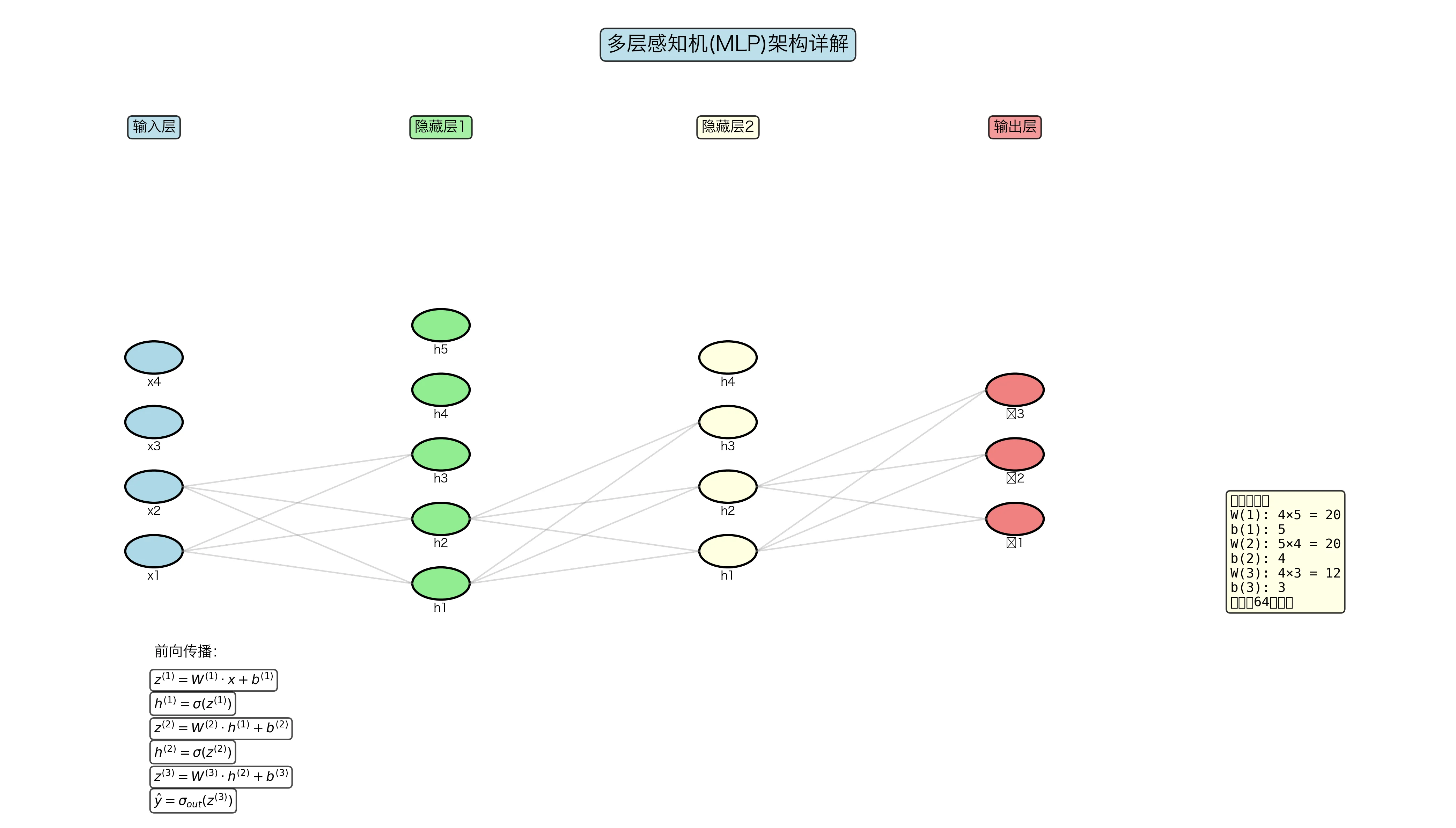
前向传播:
层 1:$\mathbf{z}^{(1)} = \mathbf{W}^{(1)} \mathbf{x} + \mathbf{b}^{(1)}$
激活:$\mathbf{h} = \sigma(\mathbf{z}^{(1)})$
层 2:$\mathbf{z}^{(2)} = \mathbf{W}^{(2)} \mathbf{h} + \mathbf{b}^{(2)}$
输出:$\hat{\mathbf{y}} = f(\mathbf{z}^{(2)})$(取决于任务,分类用 softmax,回归用恒等)
通用逼近定理(Universal Approximation Theorem):
定理:只要隐藏层足够大,单隐藏层的 MLP 可以以任意精度逼近任何连续函数。
关键前提:必须使用非线性激活函数!
为什么? 如果没有非线性激活函数(全是线性变换):
\[\mathbf{y} = \mathbf{W}^{(2)}(\mathbf{W}^{(1)}\mathbf{x} + \mathbf{b}^{(1)}) + \mathbf{b}^{(2)} = (\mathbf{W}^{(2)}\mathbf{W}^{(1)})\mathbf{x} + \ldots = \mathbf{W}_{\text{eff}}\mathbf{x} + b_{\text{eff}}\]多层退化为单层线性变换!无法学到复杂的非线性关系。
实例:解决 XOR 问题
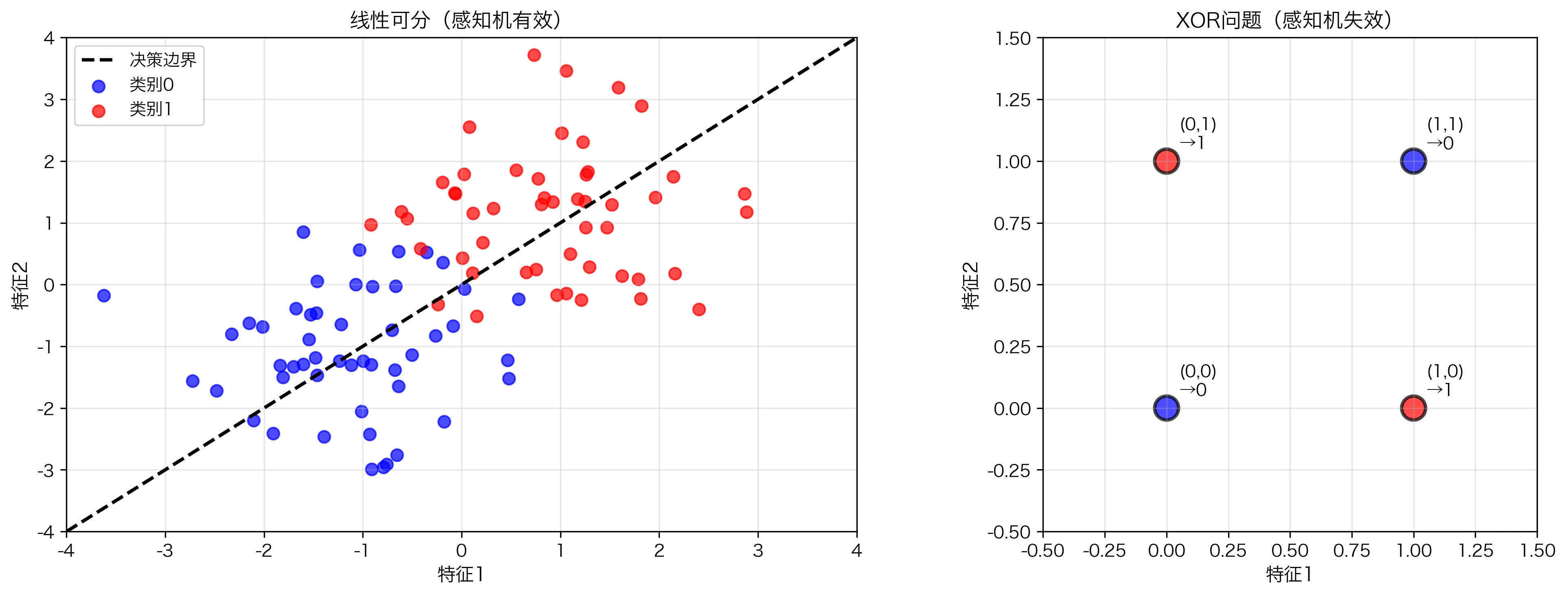
1
2
3
4
5
6
7
8
9
10
MLP 架构:2输入 → 2隐藏 → 1输出
前向传播:
z₁ = W₁·x + b₁ (2×2 矩阵 × 2维向量 = 2维)
h = σ(z₁) (应用非线性激活)
z₂ = W₂·h + b₂ (1×2 矩阵 × 2维向量 = 1维)
ŷ = sigmoid(z₂) (输出概率)
关键:隐藏层通过非线性激活,将 2D 输入"弯曲"变换,
使得原本线性不可分的数据在新空间中变得可分。
激活函数的非线性本质
为什么需要激活函数?
问题:如上所述,没有激活函数,深层网络退化为单层线性模型。
解决:引入非线性激活函数 $\sigma(\cdot)$。
函数要求:
- 非线性:$\sigma(x) \neq ax + b$(避免线性退化)
- 可导:便于反向传播计算梯度
- 计算高效:要在数百万个神经元上执行
- 梯度流通:避免梯度消失或爆炸
主要激活函数对比
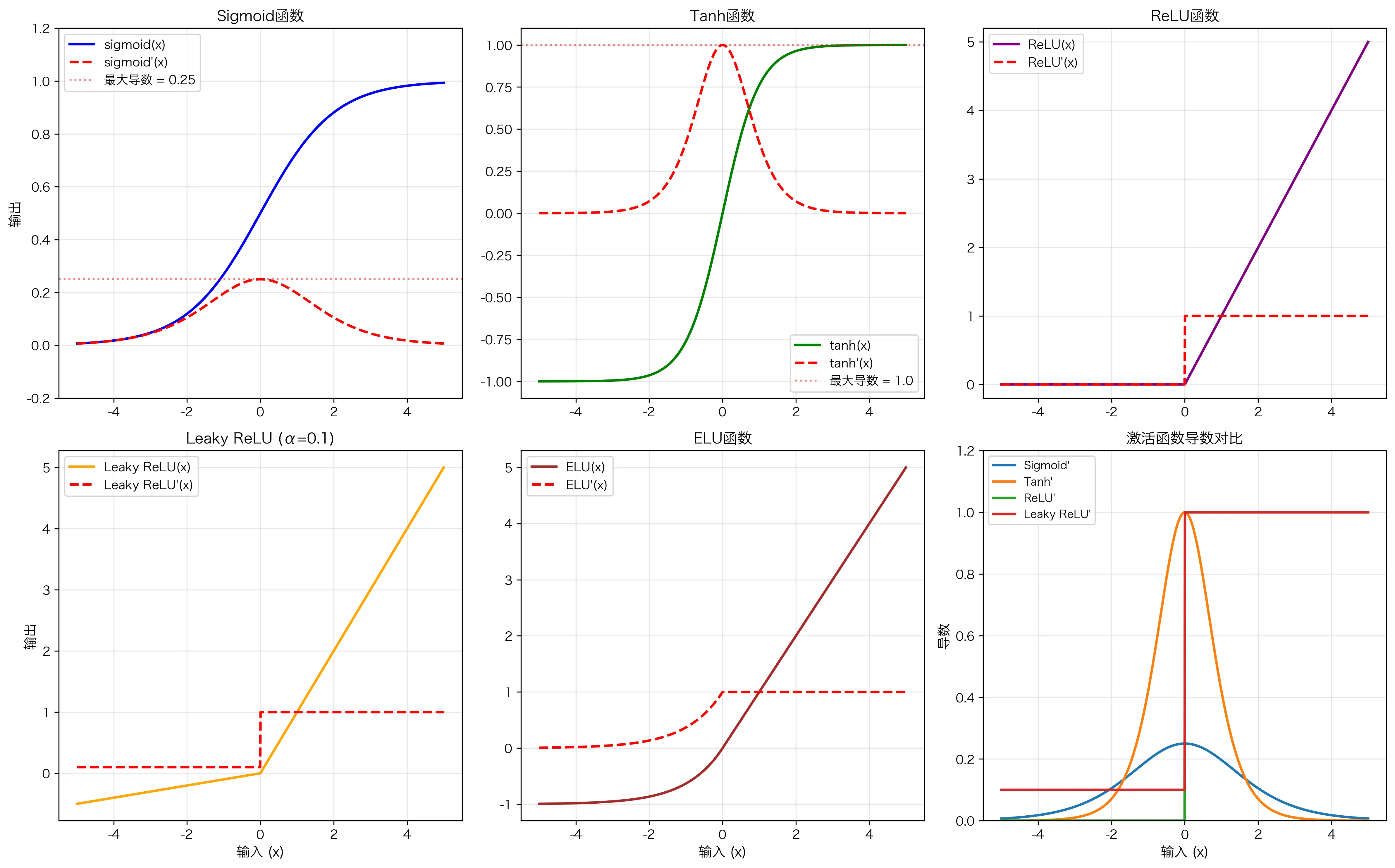
1. Sigmoid 函数
\[\sigma(x) = \frac{1}{1+e^{-x}}\] \[\sigma'(x) = \sigma(x)(1-\sigma(x))\]性质:
- 输出范围:$(0, 1)$ —— 可以解释为概率
- 导数最大值:0.25(当 $x=0$ 时)
- ✅ 早期广泛使用(逻辑回归)
- ❌ 易导致梯度消失:$\sigma’(x) \leq 0.25$
梯度消失演示:
设网络有 50 层,每层都用 Sigmoid,则:
\[\frac{\partial L}{\partial \mathbf{w}^{(1)}} \propto \prod_{l=1}^{50} \sigma'(z^{(l)}) \leq 0.25^{50} \approx 10^{-30}\]梯度几乎为零,第一层几乎无法学习!
2. Tanh 函数
\[\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = 2\sigma(2x) - 1\] \[\tanh'(x) = 1 - \tanh^2(x)\]性质:
- 输出范围:$(-1, 1)$(以零为中心,比 Sigmoid 更好)
- 导数最大值:1.0(当 $x=0$ 时)
- ✅ 比 Sigmoid 稍好,但仍有梯度消失问题
- 📊 对称性:$\tanh(-x) = -\tanh(x)$
对比:Tanh vs Sigmoid
1
2
3
4
5
6
7
8
9
10
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-4, 4, 1000)
sigmoid = 1 / (1 + np.exp(-x))
tanh = np.tanh(x)
# Sigmoid 输出在 (0, 1),平均值 0.5
# Tanh 输出在 (-1, 1),平均值 0
# 这使得 Tanh 的收敛更快
3. ReLU(Rectified Linear Unit)
\[\text{ReLU}(x) = \max(0, x)\] \[\text{ReLU}'(x) = \begin{cases} 1 & x > 0 \\ 0 & x < 0 \end{cases}\]性质:
- ✅ 导数为 1(不消失)或 0(稀疏)—— 完美解决梯度消失
- ✅ 计算简单(只需一次比较)
- ✅ 天然稀疏性(约 50% 的神经元输出为 0)
- ❌ “死亡 ReLU” 问题:$x < 0$ 时梯度为 0,若权重初始化不当,神经元可能永久死亡
1
2
3
4
5
死亡 ReLU 场景:
若某个神经元总是输出负数,其梯度永为 0,无法更新。
解决方案:
1. 仔细的权重初始化(He 初始化)
2. 使用 Leaky ReLU
4. Leaky ReLU
\[\text{Leaky ReLU}(x) = \begin{cases} x & x > 0 \\ \alpha x & x \leq 0 \end{cases}\]其中 $\alpha$ 是小的正数(通常 0.01)。
导数: \(\text{Leaky ReLU}'(x) = \begin{cases} 1 & x > 0 \\ \alpha & x \leq 0 \end{cases}\)
优点:避免了 ReLU 的死亡问题——$x < 0$ 时仍有梯度 $\alpha$。
5. ELU(Exponential Linear Unit)
\[\text{ELU}(x) = \begin{cases} x & x > 0 \\ \alpha(e^x - 1) & x \leq 0 \end{cases}\]优点:
- 负输入时平滑(导数连续)
- 输出接近零中心
- 梯度流通好
激活函数的选择指南
| 激活函数 | 梯度消失 | 计算速度 | 稀疏性 | 推荐场景 |
|---|---|---|---|---|
| Sigmoid | ❌ 严重 | 快 | 无 | 输出层(二分类) |
| Tanh | ❌ 中等 | 快 | 无 | 输出层(回归) |
| ReLU | ✅ 无 | 最快 | ✅ 高 | 隐藏层(首选) |
| Leaky ReLU | ✅ 无 | 快 | ✅ 中 | 隐藏层(替代 ReLU) |
| ELU | ✅ 无 | 较慢 | ✅ 低 | 隐藏层(精细应用) |
损失函数的选择与设计
损失函数是优化的目标,不同任务需要不同的损失函数。
1. MSE(均方误差)—— 回归任务
\[L = \text{MSE} = \frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2\]定义:预测值与真实值差的平方的平均。
梯度: \(\frac{\partial L}{\partial \hat{y}_i} = -\frac{2}{n}(y_i - \hat{y}_i)\)
性质:
- ✅ 直观、易计算
- ✅ 对大误差的惩罚更重(平方项)
- ❌ 对异常值敏感
- ❌ 当误差很大时,梯度也很大,可能导致不稳定
适用场景:连续值预测(房价、温度、股票价格等)
改进版本:RMSE(根均方误差) \(\text{RMSE} = \sqrt{\frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2}\) 优点:量纲与 $y$ 相同,易于解释。
2. Cross Entropy(交叉熵)—— 分类任务
二分类:
\[L = -\frac{1}{n}\sum_{i=1}^n [y_i \log \hat{y}_i + (1-y_i)\log(1-\hat{y}_i)]\]其中 $y_i \in {0,1}$ 是真实标签,$\hat{y}_i \in (0,1)$ 是预测概率。
多分类:
\[L = -\frac{1}{n}\sum_{i=1}^n \sum_{c=1}^C y_{ic} \log \hat{y}_{ic}\]其中 $y_{ic}$ 是独热编码(只有正确类为 1,其余为 0)。
梯度(使用 Softmax 输出时):
\[\frac{\partial L}{\partial z_k} = \hat{y}_k - y_k\]这是一个非常优美的结果!梯度就是预测和真实的差。
性质:
- ✅ 基于信息论(KL 散度)
- ✅ 梯度清晰(不会因为网络开始犯错时梯度就很小)
- ✅ 强制输出为概率分布
- ✅ 当预测错误时,损失快速增长(鼓励修正)
对比:MSE vs Cross Entropy 在分类中
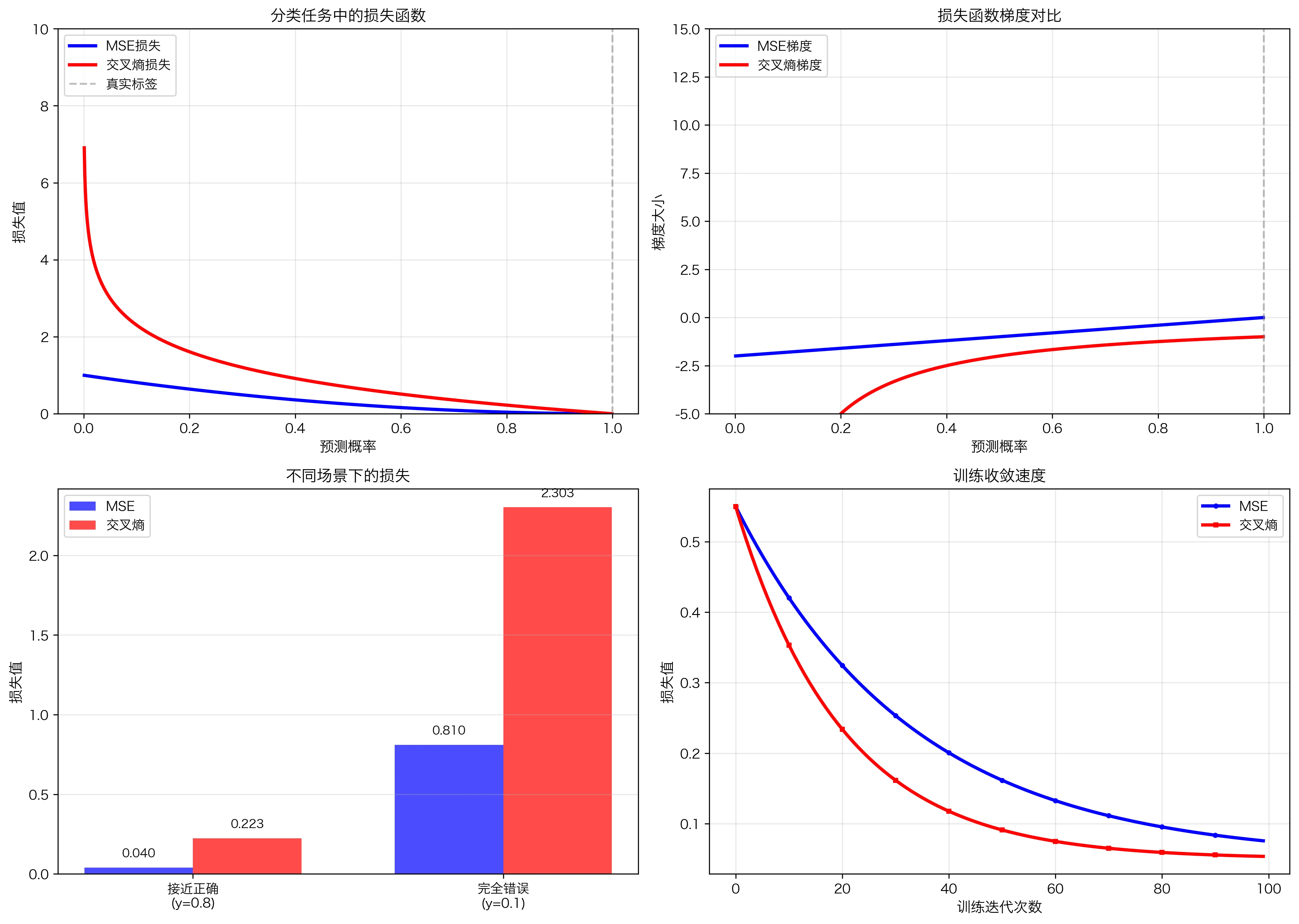
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
假设真实标签 y = [1, 0, 0](第一类)
预测结果 ŷ = [0.8, 0.1, 0.1](接近正确)
MSE = 1/3 * [(1-0.8)² + (0-0.1)² + (0-0.1)²]
= 1/3 * [0.04 + 0.01 + 0.01] = 0.0133
CrossEntropy = -[1·ln(0.8) + 0·ln(0.1) + 0·ln(0.1)]
= -ln(0.8) ≈ 0.223
现在假设预测完全错误 ŷ = [0.1, 0.6, 0.3]:
MSE = 1/3 * [(1-0.1)² + (0-0.6)² + (0-0.3)²]
= 1/3 * [0.81 + 0.36 + 0.09] = 0.42
CrossEntropy = -ln(0.1) ≈ 2.303
关键观察:
- 在第二个例子中,CrossEntropy 从 0.223 增长到 2.303(增长 10 倍)
- MSE 从 0.0133 增长到 0.42(增长 31 倍)
- CrossEntropy 的增长更"温和"且可预测,梯度更稳定
3. 其他常见损失函数
Huber Loss(robust regression): \(L = \begin{cases} \frac{1}{2}e^2 & |e| \leq \delta \\ \delta|e| - \frac{1}{2}\delta^2 & |e| > \delta \end{cases}\)
其中 $e = y - \hat{y}$ 是误差。
优点:结合了 MSE(对小误差)和 MAE(对大误差)的优点,对异常值鲁棒。
Focal Loss(处理类不平衡): \(L = -\alpha(1-p_t)^\gamma \log(p_t)\)
其中 $p_t$ 是正确类的预测概率,$\gamma$ 是聚焦参数。
优点:让模型更专注于难以分类的样本。
优化算法基础
1. 梯度下降(Gradient Descent)—— 最基础的优化
算法:
1
2
3
4
5
6
初始化参数 θ
学习率 α(超参数)
重复直到收敛:
计算梯度 g = ∇L(θ)
更新参数 θ ← θ - α·g
几何意义:每次沿梯度反方向(下降最快)走一小步。
收敛速度分析:
对于凸函数,设 Lipschitz 常数为 $\beta$,则:
- 如果学习率 $\alpha < \frac{2}{\beta}$,梯度下降收敛
- 收敛速度:$O(1/t)$($t$ 是迭代数)
问题:
- ❌ 需要计算全数据集的梯度(慢)
- ❌ 容易陷入局部最小值
- ❌ 在鞍点(saddle point)可能卡住
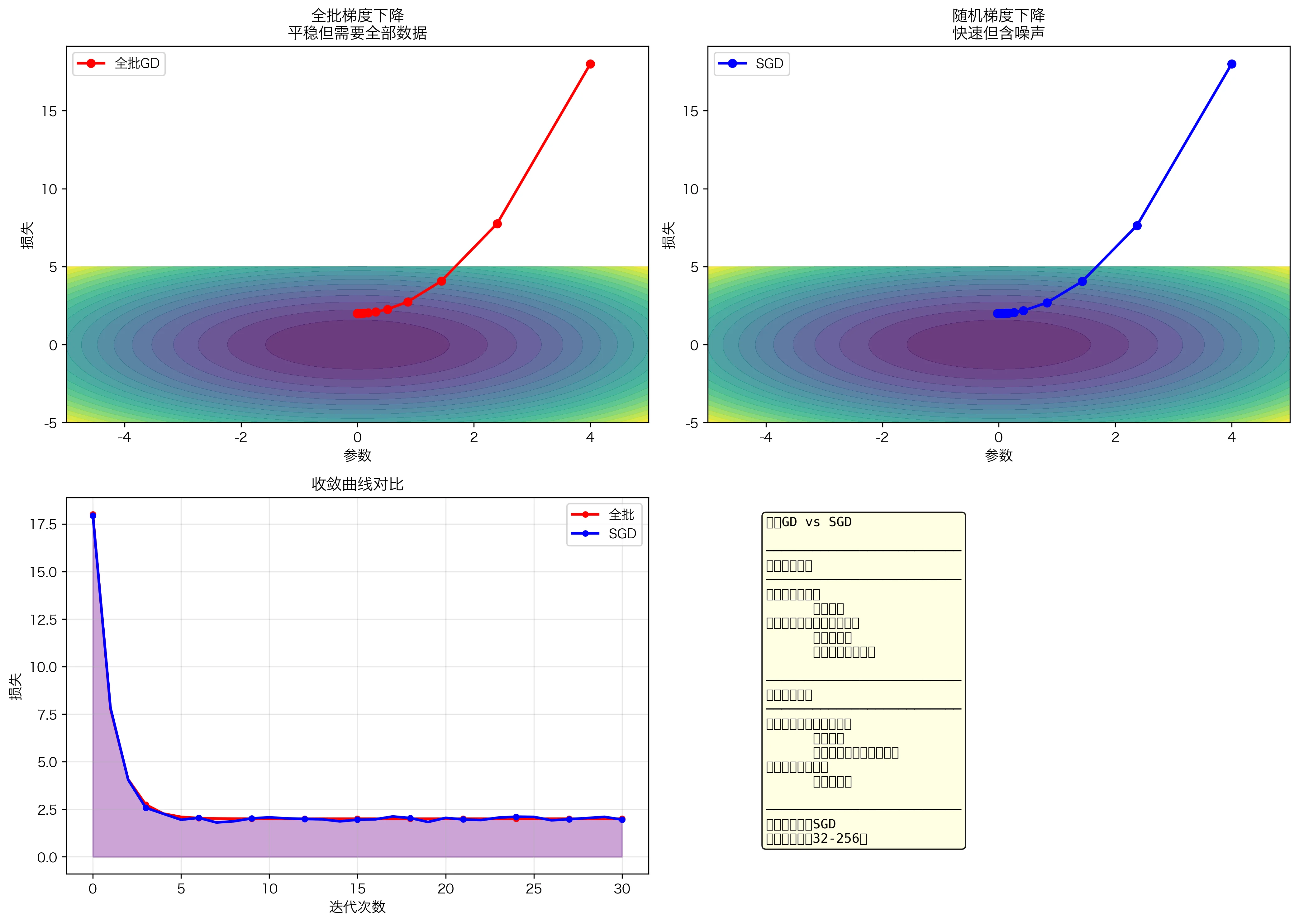
2. 随机梯度下降(SGD)—— 实践中的标准
改进:使用小批量(mini-batch)梯度而非全批量:
1
2
3
4
5
6
7
8
初始化参数 θ
学习率 α
批量大小 B
重复直到收敛:
随机采样一个小批量 {(x₁,y₁),...,(x_B,y_B)}
计算小批量梯度 g = 1/B ∑ᵢ ∇L(θ; xᵢ, yᵢ)
更新参数 θ ← θ - α·g
优势:
- ✅ 计算快(只需小批量)
- ✅ 天然的正则化效果(噪声帮助逃离局部最小值)
- ✅ 内存高效
- ✅ 可处理流数据
收敛性(随机情况下):
虽然单步噪声大,但大数定律保证: \(\mathbb{E}[g_{\text{mini-batch}}] = \nabla L(\theta)\)
平均而言,梯度方向是正确的。
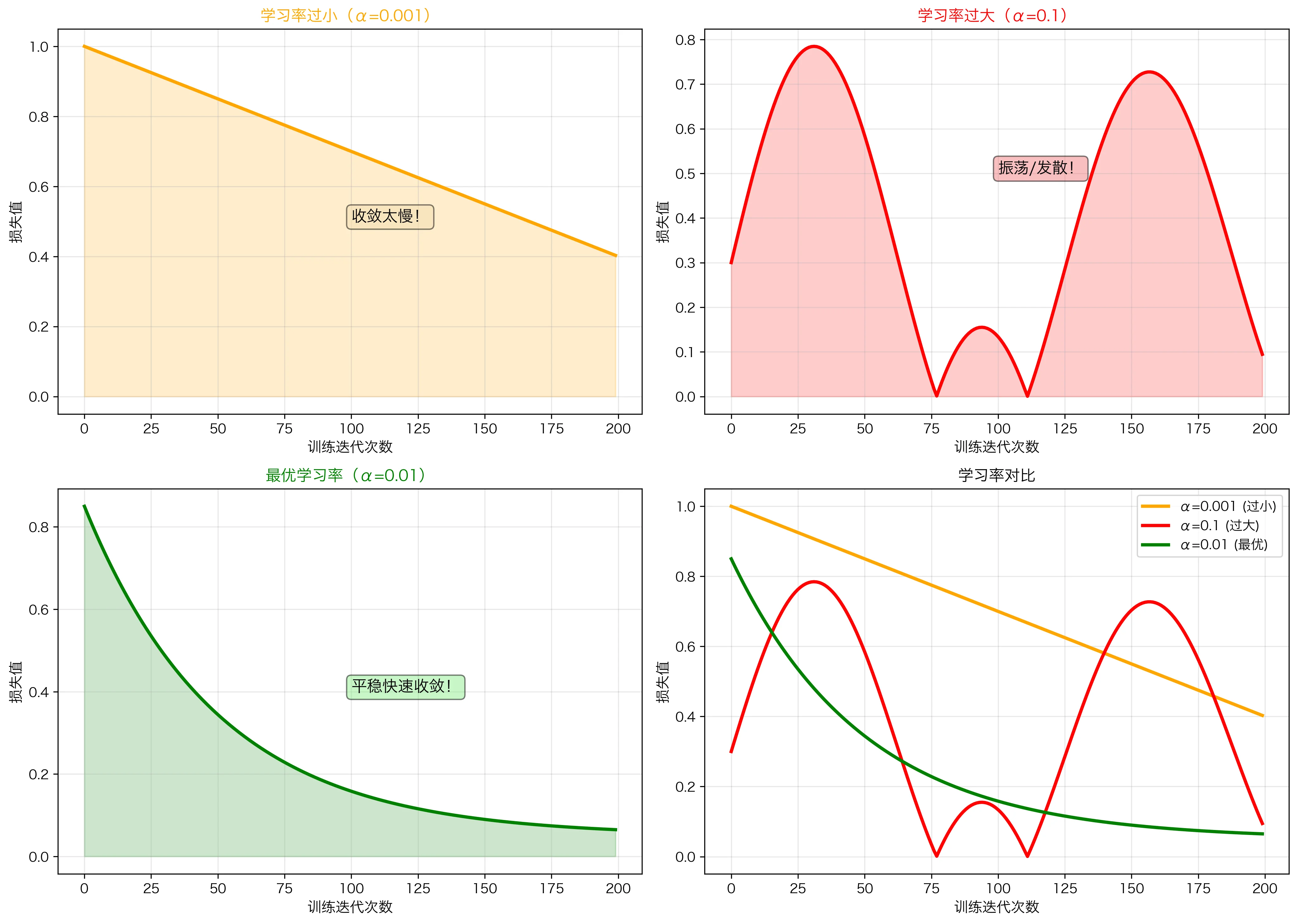
学习率的影响:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
学习率太小(α = 0.001):
- 收敛很慢
- 需要很多迭代
- 但最终能收敛
- 类似爬山爬得很慢
学习率太大(α = 0.1):
- 可能直接跳过最小值
- 损失波动剧烈
- 可能发散
- 类似大步迈,容易摔跤
最优学习率(α = 0.01):
- 快速收敛
- 损失平稳下降
反向传播算法详解
这是深度学习的灵魂。 反向传播就是链式法则的巧妙应用。
核心思想
给定计算图,反向传播按拓扑顺序的反向(从输出到输入)计算梯度。
完整例子:一个小神经网络
网络结构:
1
2
3
4
5
6
7
8
9
10
11
输入 x₁, x₂
↓
z₁ = w₁x₁ + w₂x₂ + b₁
↓
h = ReLU(z₁) (激活,引入非线性)
↓
z₂ = w₃h + b₂
↓
ŷ = sigmoid(z₂) (输出概率)
↓
L = -y·ln(ŷ) - (1-y)·ln(1-ŷ) (二元交叉熵)
前向传播(计算损失):
给定 $x_1 = 2, x_2 = 3, y = 1$(真实标签) 初始参数 $w_1=0.5, w_2=0.3, w_3=0.4, b_1=0.1, b_2=0.2$
1
2
3
4
5
Step 1: z₁ = 0.5×2 + 0.3×3 + 0.1 = 1.0 + 0.9 + 0.1 = 2.0
Step 2: h = ReLU(2.0) = 2.0 (因为 > 0)
Step 3: z₂ = 0.4×2.0 + 0.2 = 0.8 + 0.2 = 1.0
Step 4: ŷ = sigmoid(1.0) = 1/(1+e⁻¹) ≈ 0.731
Step 5: L = -1·ln(0.731) - 0·ln(0.269) ≈ 0.314
反向传播(计算梯度):
从损失开始,逐层反向计算梯度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Step 1: 损失对输出的梯度
dL/dŷ = -y/ŷ + (1-y)/(1-ŷ)
= -1/0.731 + 0/0.269
≈ -1.368
Step 2: 输出 sigmoid 的导数
dŷ/dz₂ = ŷ(1-ŷ) = 0.731 × 0.269 ≈ 0.197
(sigmoid 的导数)
Step 3: 链式法则
dL/dz₂ = dL/dŷ × dŷ/dz₂ = -1.368 × 0.197 ≈ -0.269
Step 4: z₂ 对参数和激活的梯度
dL/dw₃ = dL/dz₂ × dz₂/dw₃ = -0.269 × h = -0.269 × 2.0 ≈ -0.538
dL/db₂ = dL/dz₂ × dz₂/db₂ = -0.269 × 1 ≈ -0.269
Step 5: 反向通过激活函数(ReLU)
dL/dh = dL/dz₂ × dz₂/dh = -0.269 × w₃ = -0.269 × 0.4 ≈ -0.108
由于 h = ReLU(z₁) 且 z₁ > 0:
dL/dz₁ = dL/dh × dh/dz₁ = -0.108 × 1 ≈ -0.108
Step 6: 第一层参数梯度
dL/dw₁ = dL/dz₁ × dz₁/dw₁ = -0.108 × x₁ = -0.108 × 2 ≈ -0.216
dL/dw₂ = dL/dz₁ × dz₁/dw₂ = -0.108 × x₂ = -0.108 × 3 ≈ -0.324
dL/db₁ = dL/dz₁ × dz₁/db₁ = -0.108 × 1 ≈ -0.108
参数更新(学习率 α = 0.1):
1
2
3
4
5
w₁ ← w₁ - α·dL/dw₁ = 0.5 - 0.1×(-0.216) = 0.5 + 0.0216 = 0.5216
w₂ ← w₂ - α·dL/dw₂ = 0.3 - 0.1×(-0.324) = 0.3 + 0.0324 = 0.3324
w₃ ← w₃ - α·dL/dw₃ = 0.4 - 0.1×(-0.538) = 0.4 + 0.0538 = 0.4538
b₁ ← b₁ - α·dL/db₁ = 0.1 - 0.1×(-0.108) = 0.1 + 0.0108 = 0.1108
b₂ ← b₂ - α·dL/db₂ = 0.2 - 0.1×(-0.269) = 0.2 + 0.0269 = 0.2269
所有参数都被更新了,且由于梯度为负,更新增加了参数值。这样会减少损失(向反方向)。
反向传播的矩阵形式
对于一般的网络层:
1
2
3
4
5
6
7
8
9
前向:z^(l) = W^(l)·a^(l-1) + b^(l)
a^(l) = σ(z^(l))
反向(关键递推关系):
δ^(l) = (W^(l+1)ᵀ·δ^(l+1)) ⊙ σ'(z^(l))
参数梯度:
dL/dW^(l) = δ^(l)·(a^(l-1))ᵀ
dL/db^(l) = δ^(l)
其中:
- $\delta^{(l)} = \frac{\partial L}{\partial z^{(l)}}$ 是损失对预激活值的梯度
- $⊙$ 是逐元素乘积(Hadamard 积)
- $σ’(z^{(l)})$ 是激活函数的导数
反向传播的计算复杂性
前向传播:$O(总权重数)$
反向传播:$O(总权重数)$ —— 几乎相同!
这就是反向传播高效的原因:它与前向传播有相同的复杂度,但计算了所有参数的梯度。
实现细节:数值稳定性
问题:梯度可能非常小或非常大
解决方案 1:梯度归一化
1
2
if ||gradient|| > threshold:
gradient = gradient / ||gradient|| * threshold
解决方案 2:梯度裁剪(Gradient Clipping)
1
gradient = np.clip(gradient, -clip_value, clip_value)
解决方案 3:批量归一化
1
归一化每层的输入(后续详细讲解)
小结:算法层的完整流程
1
2
3
4
1. 前向传播:输入 → 计算每层激活 → 计算损失
2. 反向传播:损失 → 链式法则 → 计算所有参数梯度
3. 参数更新:使用梯度下降(或变种如 Adam)更新参数
4. 重复:循环多个 epoch 直到收敛
关键数学引理:
| 步骤 | 数学 | 计算效率 |
|---|---|---|
| 前向 | $a^{(l)} = \sigma(W^{(l)}a^{(l-1)} + b^{(l)})$ | $O(N)$(矩阵乘法) |
| 反向 | $\delta^{(l)} = (W^{(l+1)T}\delta^{(l+1)})⊙\sigma’(z^{(l)})$ | $O(N)$(同样操作) |
| 更新 | $\theta ← \theta - α∇L$ | $O(N)$(逐元素) |
这三个步骤都是线性复杂度,因此总时间复杂度为 $O(N)$,其中 $N$ 是参数总数。
第一部分:微积分基础
1.1 导数的严格定义
定义:函数 $f: \mathbb{R} \to \mathbb{R}$ 在点 $x_0$ 处的导数定义为:
\[f'(x_0) = \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h}\]深层含义:
- 导数衡量函数在该点的瞬时变化率
- 几何意义是曲线在该点的切线斜率
- 在深度学习中,$\nabla f$ 指向损失函数增长最快的方向
在深度学习中的体现: 如果我们的损失函数是 $L(\theta)$,其中 $\theta$ 是模型参数,那么 $\frac{\partial L}{\partial \theta}$ 告诉我们改变参数如何影响损失。
1.2 多元函数的偏导数
对于函数 $f: \mathbb{R}^n \to \mathbb{R}$,偏导数定义为:
\[\frac{\partial f}{\partial x_i} = \lim_{h \to 0} \frac{f(x_1, \ldots, x_i + h, \ldots, x_n) - f(x_1, \ldots, x_n)}{h}\]梯度向量(梯度是所有偏导数的集合):
\[\nabla f = \begin{pmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots \\ \frac{\partial f}{\partial x_n} \end{pmatrix}\]性质:
- 梯度 $\nabla f$ 永远指向函数增长最快的方向
- 梯度的模 $|\nabla f|$ 表示增长的速率
- 负梯度 $-\nabla f$ 指向函数下降最快的方向
在神经网络中:一个简单的 2 层网络有数百万个参数,梯度就是这几百万个偏导数组成的向量。
1.3 Jacobian 矩阵与 Hessian 矩阵
Jacobian 矩阵:对于向量函数 $\mathbf{f}: \mathbb{R}^n \to \mathbb{R}^m$:
\[J = \begin{pmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{pmatrix}\]意义:在神经网络的反向传播中,Jacobian 矩阵描述了每一层输出对输入的导数。
Hessian 矩阵:对于标量函数 $f: \mathbb{R}^n \to \mathbb{R}$,二阶导数矩阵:
\[H = \begin{pmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{pmatrix}\]意义:Hessian 矩阵描述了损失函数的曲率,对于理解二阶优化方法(如 Newton 方法)至关重要。
1.4 方向导数与梯度的关系
对于单位方向向量 $\mathbf{u}$,方向导数为:
\[D_{\mathbf{u}}f = \nabla f \cdot \mathbf{u} = \|\nabla f\| \cos(\theta)\]其中 $\theta$ 是梯度与方向向量的夹角。
关键洞察:
- 当 $\theta = 0$ 时(沿梯度方向),方向导数最大,函数增长最快
- 当 $\theta = 180°$ 时(沿负梯度方向),函数下降最快
- 这正是梯度下降算法的理论基础!
第二部分:链式法则与反向传播
2.1 一维情况下的链式法则
基础形式:设 $y = f(g(x))$,则:
\[\frac{dy}{dx} = \frac{dy}{dg} \cdot \frac{dg}{dx}\]具体例子: \(y = \sin(x^2)\)
使用链式法则: \(\frac{dy}{dx} = \cos(x^2) \cdot 2x\)
2.2 多元函数的链式法则(矩阵形式)
设 $\mathbf{y} = f(g(\mathbf{x}))$,其中:
- $\mathbf{x} \in \mathbb{R}^n$
- $\mathbf{g}: \mathbb{R}^n \to \mathbb{R}^m$
- $f: \mathbb{R}^m \to \mathbb{R}$
则偏导数满足链式法则:
\[\frac{\partial f}{\partial x_i} = \sum_{j=1}^{m} \frac{\partial f}{\partial g_j} \cdot \frac{\partial g_j}{\partial x_i}\]用矩阵表示:
\[\nabla_{\mathbf{x}} f = J_g^T \nabla_{\mathbf{g}} f\]其中 $J_g$ 是 $g$ 的 Jacobian 矩阵。
2.3 计算图与自动微分
计算图是表示函数复合的有向无环图。每个节点表示一个操作或变量,边表示数据流。
例子:计算 $z = (x + y) \cdot (y + 1)$
1
2
3
4
5
6
7
8
9
10
11
12
13
x y
\ /
(add)
|
u ——————┐
|
y -- (add)
|
v
|
(mul)
|
z
正向传播(Forward Pass): \(u = x + y = 2 + 3 = 5\) \(v = y + 1 = 3 + 1 = 4\) \(z = u \cdot v = 5 \cdot 4 = 20\)
反向传播(Backward Pass),计算 $\frac{\partial z}{\partial x}$, $\frac{\partial z}{\partial y}$:
-
初始化:$\frac{\partial z}{\partial z} = 1$
- 乘法节点:
- $\frac{\partial z}{\partial u} = v = 4$
- $\frac{\partial z}{\partial v} = u = 5$
- 加法节点(左边):
- $\frac{\partial z}{\partial x} = \frac{\partial z}{\partial u} \cdot \frac{\partial u}{\partial x} = 4 \cdot 1 = 4$
- $\frac{\partial z}{\partial y} = \frac{\partial z}{\partial u} \cdot \frac{\partial u}{\partial y} = 4 \cdot 1 = 4$
- 加法节点(右边):
- $\frac{\partial z}{\partial y} \text{(from right)} = \frac{\partial z}{\partial v} \cdot \frac{\partial v}{\partial y} = 5 \cdot 1 = 5$
- 累加:$\frac{\partial z}{\partial y} = 4 + 5 = 9$
最终结果:$\frac{\partial z}{\partial x} = 4$,$\frac{\partial z}{\partial y} = 9$
2.4 神经网络中的反向传播
对于一个 $L$ 层的神经网络:
\(\mathbf{z}^{(l)} = \mathbf{W}^{(l)} \mathbf{a}^{(l-1)} + \mathbf{b}^{(l)}\) \(\mathbf{a}^{(l)} = \sigma(\mathbf{z}^{(l)})\)
其中 $\sigma$ 是激活函数(如 ReLU、Sigmoid 等)。
反向传播的核心递推关系:
\[\delta^{(l)} = (\mathbf{W}^{(l+1)T} \delta^{(l+1)}) \odot \sigma'(\mathbf{z}^{(l)})\]这里:
- $\delta^{(l)} = \frac{\partial L}{\partial \mathbf{z}^{(l)}}$ 是损失对第 $l$ 层预激活值的梯度
- $\odot$ 表示逐元素乘积(Hadamard 积)
- $\sigma’$ 是激活函数的导数
参数梯度:
\(\frac{\partial L}{\partial \mathbf{W}^{(l)}} = \delta^{(l)} \mathbf{a}^{(l-1)T}\) \(\frac{\partial L}{\partial \mathbf{b}^{(l)}} = \delta^{(l)}\)
关键洞察:反向传播本质上就是链式法则的递归应用!每一层计算自己的梯度时,都使用上一层已经计算好的梯度。
2.5 梯度消失与梯度爆炸问题
梯度消失问题:
当网络很深时,由于链式法则中有连续的乘法:
\[\frac{\partial L}{\partial \mathbf{W}^{(1)}} = \frac{\partial L}{\partial \mathbf{a}^{(L)}} \prod_{l=2}^{L} \frac{\partial \mathbf{a}^{(l)}}{\partial \mathbf{z}^{(l)}} \frac{\partial \mathbf{z}^{(l)}}{\partial \mathbf{a}^{(l-1)}}\]如果每个 $\frac{\partial \mathbf{a}^{(l)}}{\partial \mathbf{z}^{(l)}}$ 都小于 1(如使用 Sigmoid 函数,其导数最大为 0.25),则乘积会以指数速度衰减。
数学表述:设 $\sigma’(z) \leq 0.25$,则:
\[\left\|\frac{\partial L}{\partial \mathbf{W}^{(1)}}\right\| \leq 0.25^L \left\|\frac{\partial L}{\partial \mathbf{a}^{(L)}}\right\|\]当 $L = 50$ 时,$0.25^{50} \approx 10^{-30}$,梯度几乎完全消失!
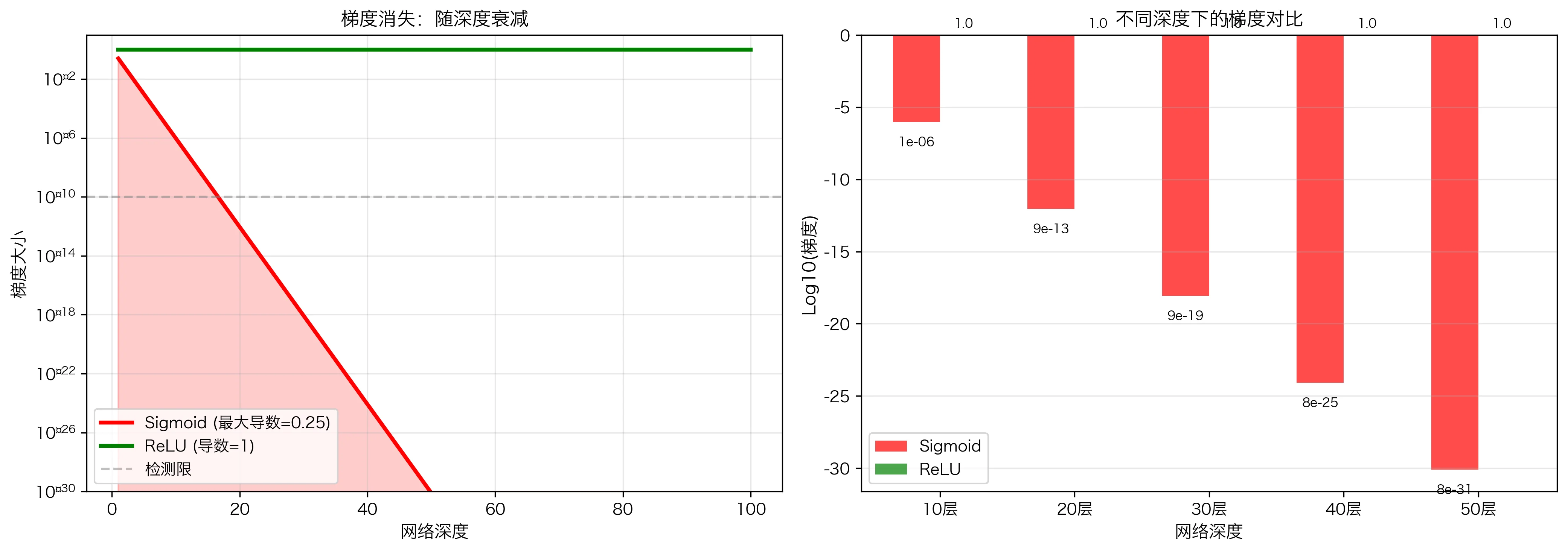
解决方案:
- 使用 ReLU 激活函数(导数为 0 或 1,不会衰减)
- 批量归一化(Batch Normalization)
- 残差连接(Residual Connections)
第三部分:梯度下降与优化
3.1 梯度下降的几何直观
梯度下降算法的更新规则:
\[\theta_{t+1} = \theta_t - \alpha \nabla L(\theta_t)\]其中 $\alpha$ 是学习率。
几何意义:每次迭代,我们沿着损失函数梯度的反方向移动 $\alpha$ 的距离。
3.2 收敛性分析
定理(Gradient Descent 收敛性):假设 $L(\theta)$ 是 $\beta$-光滑的(即 Lipschitz 连续梯度),$\alpha < \frac{2}{\beta}$,则梯度下降收敛到临界点。
光滑性的定义:函数 $L$ 是 $\beta$-光滑的,当且仅当:
\[\|\nabla L(\theta_1) - \nabla L(\theta_2)\| \leq \beta \|\theta_1 - \theta_2\|\]收敛率:对于强凸函数,收敛率为指数级的(线性收敛):
\[L(\theta_t) - L(\theta^*) \leq (1 - \frac{2\alpha \mu}{\beta})^t (L(\theta_0) - L(\theta^*))\]其中 $\mu$ 是强凸系数,$\theta^*$ 是最优解。
3.3 随机梯度下降(SGD)
由于神经网络通常在大数据集上训练,我们使用 SGD 而非全量梯度下降:
\[\theta_{t+1} = \theta_t - \alpha \nabla L_{\text{batch}}(\theta_t)\]其中 $L_{\text{batch}} = \frac{1}{B} \sum_{i \in \text{batch}} L_i(\theta_t)$ 是一个随机小批量上的损失。
随机性的作用:
- 减少内存占用
- 引入噪声,有助于逃离局部最小值
- 天然的正则化效果
3.4 动量方法(Momentum)
基础梯度下降的问题:在”之字形”的山谷中振荡剧烈。
带动量的更新:
\(\mathbf{v}_{t+1} = \gamma \mathbf{v}_t + \nabla L(\theta_t)\) \(\theta_{t+1} = \theta_t - \alpha \mathbf{v}_{t+1}\)
其中 $\gamma \in (0, 1)$ 是动量系数,通常取 0.9。
数学直观:可以看作是一个低通滤波器,抑制高频振荡,保留低频趋势。
加权平均解释:
\[\mathbf{v}_{t+1} = \sum_{j=0}^{t} \gamma^j \nabla L(\theta_{t-j})\]历史梯度的权重呈指数衰减,最近的梯度权重最大。
3.5 Adam 优化器的完整数学推导
Adam(Adaptive Moment Estimation)结合了 RMSprop 和 Momentum 的思想。
核心思想:维护梯度的一阶矩(均值)和二阶矩(方差)的指数移动平均。
更新规则:
\(m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t\) \(v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2\)
其中 $g_t = \nabla L(\theta_t)$ 是时间 $t$ 的梯度。
偏差校正: 由于 $m_0 = 0$,$v_0 = 0$,初期会严重向零偏移。因此需要校正:
\(\hat{m}_t = \frac{m_t}{1 - \beta_1^t}\) \(\hat{v}_t = \frac{v_t}{1 - \beta_2^t}\)
参数更新:
\[\theta_{t+1} = \theta_t - \alpha \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}\]其中 $\epsilon$ 是一个小常数(通常 $10^{-8}$)防止除以零。
直观理解:
- 分子 $\hat{m}_t$ 是一个”加权移动平均”的梯度,提供方向性
- 分母 $\sqrt{\hat{v}_t}$ 是梯度幅度的自适应学习率,对梯度大的参数降低学习率
第四部分:损失函数与信息论
4.1 交叉熵损失的推导
在分类任务中,真实标签是概率分布 $p(x)$,模型预测是 $q(x)$。
KL 散度(相对熵):衡量两个概率分布的差异
\[D_{KL}(p \| q) = \sum_x p(x) \log \frac{p(x)}{q(x)} = H(p, q) - H(p)\]其中:
- $H(p, q) = -\sum_x p(x) \log q(x)$ 是交叉熵
- $H(p) = -\sum_x p(x) \log p(x)$ 是 $p$ 的熵
由于 $H(p)$ 是常数(真实分布固定),最小化 KL 散度等价于最小化交叉熵:
\[L = H(p, q) = -\sum_{c=1}^C y_c \log \hat{y}_c\]其中 $y_c$ 是第 $c$ 类的真实标签(独热编码),$\hat{y}_c$ 是模型预测的概率。
4.2 Softmax 函数与梯度计算
对于多分类问题,输出层使用 softmax 函数:
\[\hat{y}_i = \frac{e^{z_i}}{\sum_{j=1}^C e^{z_j}}\]其中 $z_i$ 是第 $i$ 个类的输出层预激活值。
梯度计算(对数据流非常重要):
\[\frac{\partial L}{\partial z_i} = \hat{y}_i - y_i\]推导(简化形式):
\[\frac{\partial L}{\partial z_i} = -\sum_{c=1}^C y_c \frac{\partial \log \hat{y}_c}{\partial z_i}\]由于 $y$ 是独热编码,只有真实类 $k$ 对应的 $y_k = 1$:
\[\frac{\partial L}{\partial z_i} = -\frac{\partial \log \hat{y}_k}{\partial z_i}\]使用链式法则和 softmax 的导数性质:
\[\frac{\partial \log \hat{y}_k}{\partial z_i} = \frac{\partial \log \hat{y}_k}{\partial \hat{y}_k} \cdot \frac{\partial \hat{y}_k}{\partial z_i} = \frac{1}{\hat{y}_k} \cdot \frac{\partial \hat{y}_k}{\partial z_i}\]经过复杂的计算可得:
\[\frac{\partial L}{\partial z_i} = \hat{y}_i - y_i\]关键特性:梯度是预测概率与真实标签的差!这在直观上也很合理:错误越大,梯度越大。
4.3 L2 正则化的贝叶斯解释
L2 正则化损失:
\[L_{\text{total}} = L(y, \hat{y}) + \lambda \|\theta\|_2^2\]从贝叶斯角度:假设参数服从高斯先验 $p(\theta) = \mathcal{N}(0, \sigma^2)$,则:
\[-\log p(\theta | D) = -\log p(D | \theta) - \log p(\theta) + \text{const}\]其中:
-
$-\log p(D \theta) \propto L(y, \hat{y})$ 是数据似然的负对数 - $-\log p(\theta) = \frac{|\theta|_2^2}{2\sigma^2}$ 是高斯先验的负对数
因此,最大后验概率(MAP)估计等价于:
\[\min_\theta L(y, \hat{y}) + \frac{1}{2\sigma^2} \|\theta\|_2^2\]这正是 L2 正则化!参数 $\lambda = \frac{1}{2\sigma^2}$ 反映了我们对参数大小的先验信念。
第五部分:实际案例——从理论到代码
5.1 案例:图像分类中的数学应用
背景:使用 CNN 对 CIFAR-10 数据集进行分类。
模型架构:
1
2
3
4
5
6
7
8
9
10
11
12
输入 (32×32×3)
→ Conv(3→32, kernel=3)
→ ReLU
→ MaxPool(2×2)
→ Conv(32→64, kernel=3)
→ ReLU
→ MaxPool(2×2)
→ Flatten
→ Dense(64→128)
→ ReLU
→ Dense(128→10)
→ Softmax
5.2 卷积层的数学表述
卷积操作(单个输出):
\[y[i,j] = \sum_{m=0}^{K-1} \sum_{n=0}^{K-1} w[m,n] \cdot x[i+m, j+n] + b\]其中 $K$ 是卷积核大小,$w$ 是卷积核参数,$b$ 是偏置。
完整形式(对所有输出通道):
\[y^{(l)}[i,j,c_{\text{out}}] = \sum_{c_{\text{in}}=1}^{C_{\text{in}}} \sum_{m=0}^{K-1} \sum_{n=0}^{K-1} w^{(l)}[m,n,c_{\text{in}},c_{\text{out}}] \cdot x^{(l-1)}[i+m, j+n, c_{\text{in}}] + b^{(l)}[c_{\text{out}}]\]参数数量:$K \times K \times C_{\text{in}} \times C_{\text{out}}$
对于 $3 \times 3$ 卷积从 32 通道到 64 通道:$3 \times 3 \times 32 \times 64 = 18432$ 个参数。
5.3 反向传播详细过程
前向传播流程:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
输入 x
↓
z₁ = Conv(x) ← 32 个特征图,每个 30×30
↓
a₁ = ReLU(z₁) ← ReLU 激活
↓
p₁ = MaxPool(a₁) ← 最大池化,15×15
↓
z₂ = Conv(p₁) ← 64 个特征图,13×13
↓
a₂ = ReLU(z₂)
↓
p₂ = MaxPool(a₂) ← 最大池化,6×6
↓
f = Flatten(p₂) ← 展平:6×6×64 = 2304 维
↓
h = Dense(f) ← 128 维隐藏层
↓
z₃ = ReLU(h)
↓
logits = Dense(z₃) ← 10 维类别得分
↓
probs = Softmax(logits) ← 概率分布
↓
L = CrossEntropy(probs, y_true) ← 损失
反向传播详细计算:
-
输出层梯度(已在 4.2 节推导): \(\delta_{\text{logits}} = \text{probs} - y_{\text{true}}\)
-
倒数第二层梯度(使用链式法则): \(\delta_h = \delta_{\text{logits}} \cdot W_{\text{Dense}}^T\) \(\delta_{z_3} = \delta_h \odot \mathbb{1}_{h > 0}\) (ReLU 的导数)
-
展平层反向(重塑梯度): \(\delta_{p_2} = \text{reshape}(\delta_{z_3}, \text{shape}(p_2))\)
-
最大池化反向(只有在正向传播中是最大值的位置有梯度): \(\delta_{a_2}[i,j] = \begin{cases} \delta_{p_2}[i',j'] & \text{if } (i,j) = \arg\max \\ 0 & \text{otherwise} \end{cases}\)
-
第二卷积层反向(需要通过卷积求梯度,涉及”转置卷积”):
对于卷积参数的梯度: \(\frac{\partial L}{\partial w^{(2)}} = \text{ConvTranspose}(p_1, \delta_{a_2})\)
对于输入的梯度(传播到前一层): \(\delta_{p_1} = \text{ConvTranspose}(w^{(2)}, \delta_{a_2})\)
5.4 完整的 Python 实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
import numpy as np
from scipy import signal
class ConvLayer:
"""卷积层的完整实现,展示数学细节"""
def __init__(self, in_channels, out_channels, kernel_size=3):
"""
初始化卷积层参数
使用 He 初始化确保梯度的适当缩放
"""
self.in_channels = in_channels
self.out_channels = out_channels
self.kernel_size = kernel_size
# He 初始化:方差为 2/(fan_in)
fan_in = in_channels * kernel_size * kernel_size
stddev = np.sqrt(2.0 / fan_in)
# 形状:(kernel_size, kernel_size, in_channels, out_channels)
self.W = np.random.randn(
kernel_size, kernel_size, in_channels, out_channels
) * stddev
self.b = np.zeros(out_channels)
# 保存中间值用于反向传播
self.cache = {}
def forward(self, x):
"""
前向传播:x 的形状为 (batch_size, height, width, channels)
"""
batch_size, height, width, _ = x.shape
# 输出大小(假设 padding=0, stride=1)
out_height = height - self.kernel_size + 1
out_width = width - self.kernel_size + 1
output = np.zeros((
batch_size, out_height, out_width, self.out_channels
))
# 对每个样本、每个输出位置、每个输出通道执行卷积
for b in range(batch_size):
for out_c in range(self.out_channels):
for i in range(out_height):
for j in range(out_width):
# 提取 patch
patch = x[b, i:i+self.kernel_size, j:j+self.kernel_size, :]
# 逐通道卷积和求和
conv_sum = 0
for in_c in range(self.in_channels):
conv_sum += np.sum(
patch[:, :, in_c] * self.W[:, :, in_c, out_c]
)
output[b, i, j, out_c] = conv_sum + self.b[out_c]
self.cache['x'] = x
return output
def backward(self, dL_dout):
"""
反向传播:计算损失对参数和输入的梯度
dL_dout 形状:(batch_size, out_height, out_width, out_channels)
"""
batch_size, out_height, out_width, out_channels = dL_dout.shape
x = self.cache['x']
_, height, width, in_channels = x.shape
# 初始化梯度
dL_dW = np.zeros_like(self.W)
dL_db = np.zeros_like(self.b)
dL_dx = np.zeros_like(x)
# 计算参数梯度和输入梯度
for b in range(batch_size):
for out_c in range(out_channels):
for i in range(out_height):
for j in range(out_width):
# 提取 patch
patch = x[b, i:i+self.kernel_size, j:j+self.kernel_size, :]
grad = dL_dout[b, i, j, out_c]
# 参数梯度:局部梯度 × 输入 patch
for in_c in range(in_channels):
dL_dW[:, :, in_c, out_c] += grad * patch[:, :, in_c]
# 输入梯度:局部梯度 × 权重
dL_dx[b, i:i+self.kernel_size, j:j+self.kernel_size, :] += (
grad * self.W[:, :, :, out_c]
)
# 偏置梯度:对所有空间位置求和
dL_db[out_c] = np.sum(dL_dout[:, :, :, out_c])
return dL_dx, dL_dW, dL_db
def update(self, dL_dW, dL_db, learning_rate=0.01):
"""使用梯度下降更新参数"""
self.W -= learning_rate * dL_dW
self.b -= learning_rate * dL_db
class DenseLayer:
"""全连接层"""
def __init__(self, in_features, out_features):
"""初始化参数"""
stddev = np.sqrt(2.0 / in_features) # He 初始化
self.W = np.random.randn(in_features, out_features) * stddev
self.b = np.zeros(out_features)
self.cache = {}
def forward(self, x):
"""前向传播"""
# x 形状:(batch_size, in_features)
z = np.dot(x, self.W) + self.b
self.cache['x'] = x
return z
def backward(self, dL_dz):
"""
反向传播
这是一个最清晰的线性变换梯度例子:
如果 z = x·W + b,则
dL/dW = x^T · dL/dz (外积)
dL/dx = dL/dz · W^T
"""
x = self.cache['x']
batch_size = x.shape[0]
# 参数梯度
dL_dW = np.dot(x.T, dL_dz) / batch_size
dL_db = np.sum(dL_dz, axis=0) / batch_size
# 输入梯度(传播到前一层)
dL_dx = np.dot(dL_dz, self.W.T)
return dL_dx, dL_dW, dL_db
def update(self, dL_dW, dL_db, learning_rate=0.01):
"""参数更新"""
self.W -= learning_rate * dL_dW
self.b -= learning_rate * dL_db
class ReLULayer:
"""ReLU 激活函数"""
def __init__(self):
self.cache = {}
def forward(self, x):
"""
前向传播:a = max(0, x)
"""
self.cache['x'] = x
return np.maximum(0, x)
def backward(self, dL_da):
"""
反向传播:
dL/dx = dL/da · da/dx
其中 da/dx = 1 if x > 0 else 0
"""
x = self.cache['x']
return dL_da * (x > 0).astype(float)
class SoftmaxCrossEntropyLoss:
"""
Softmax + CrossEntropy 组合层
这是数值稳定的实现(避免溢出)
"""
def forward(self, logits, labels):
"""
输入:
logits:原始输出,形状 (batch_size, num_classes)
labels:独热编码标签,形状 (batch_size, num_classes)
返回:损失值
"""
batch_size = logits.shape[0]
# 数值稳定的 softmax:减去最大值
max_logits = np.max(logits, axis=1, keepdims=True)
exp_logits = np.exp(logits - max_logits)
probs = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
# 交叉熵损失
loss = -np.sum(labels * np.log(probs + 1e-8)) / batch_size
self.cache = {'probs': probs, 'labels': labels}
return loss
def backward(self):
"""
返回损失对 logits 的梯度
这正是我们在 4.2 节推导的优美结果:
dL/dlogits = probs - labels
"""
probs = self.cache['probs']
labels = self.cache['labels']
return (probs - labels) / labels.shape[0]
# ============ 完整的训练循环 ============
class SimpleConvNet:
"""简化的 CNN 用于演示数学原理"""
def __init__(self):
# 第一个卷积块
self.conv1 = ConvLayer(in_channels=3, out_channels=32, kernel_size=3)
self.relu1 = ReLULayer()
# 第二个卷积块(省略 MaxPool 以简化)
self.conv2 = ConvLayer(in_channels=32, out_channels=64, kernel_size=3)
self.relu2 = ReLULayer()
# 全连接层
# 假设经过卷积后的特征是 (64, 26, 26)
self.dense1 = DenseLayer(in_features=64*26*26, out_features=128)
self.relu3 = ReLULayer()
self.dense2 = DenseLayer(in_features=128, out_features=10)
# 损失函数
self.loss_fn = SoftmaxCrossEntropyLoss()
def forward(self, x):
"""前向传播"""
# 第一个卷积块
z1 = self.conv1.forward(x)
a1 = self.relu1.forward(z1)
# 第二个卷积块
z2 = self.conv2.forward(a1)
a2 = self.relu2.forward(z2)
# 展平
batch_size = a2.shape[0]
a2_flat = a2.reshape(batch_size, -1)
# 全连接层
z3 = self.dense1.forward(a2_flat)
a3 = self.relu3.forward(z3)
logits = self.dense2.forward(a3)
return logits
def backward(self, logits, labels):
"""反向传播"""
# 计算损失
loss = self.loss_fn.forward(logits, labels)
# 从损失开始的梯度
dL_dlogits = self.loss_fn.backward()
# 通过 dense2 反向传播
dL_da3, dL_dW2, dL_db2 = self.dense2.backward(dL_dlogits)
# 通过 relu3 反向传播
dL_dz3 = self.relu3.backward(dL_da3)
# 通过 dense1 反向传播
dL_da2_flat, dL_dW1, dL_db1 = self.dense1.backward(dL_dz3)
# 重塑为卷积输出的形状
batch_size = dL_da2_flat.shape[0]
dL_da2 = dL_da2_flat.reshape(batch_size, 26, 26, 64)
# 通过 relu2 反向传播
dL_dz2 = self.relu2.backward(dL_da2)
# 通过 conv2 反向传播
dL_da1, dL_dW_conv2, dL_db_conv2 = self.conv2.backward(dL_dz2)
# 通过 relu1 反向传播
dL_dz1 = self.relu1.backward(dL_da1)
# 通过 conv1 反向传播
dL_dx, dL_dW_conv1, dL_db_conv1 = self.conv1.backward(dL_dz1)
return loss, {
'conv1': (dL_dW_conv1, dL_db_conv1),
'conv2': (dL_dW_conv2, dL_db_conv2),
'dense1': (dL_dW1, dL_db1),
'dense2': (dL_dW2, dL_db2)
}
def update_parameters(self, gradients, learning_rate=0.01):
"""使用梯度下降更新参数"""
self.conv1.update(*gradients['conv1'], learning_rate)
self.conv2.update(*gradients['conv2'], learning_rate)
self.dense1.update(*gradients['dense1'], learning_rate)
self.dense2.update(*gradients['dense2'], learning_rate)
def train_step(self, x_batch, y_batch, learning_rate=0.01):
"""单个训练步骤"""
# 前向传播
logits = self.forward(x_batch)
# 反向传播
loss, gradients = self.backward(logits, y_batch)
# 参数更新
self.update_parameters(gradients, learning_rate)
return loss
# ============ 训练示例 ============
if __name__ == "__main__":
# 创建模型
model = SimpleConvNet()
# 模拟数据(实际中应使用真实的 CIFAR-10 数据)
batch_size = 4
x_batch = np.random.randn(batch_size, 32, 32, 3) * 0.1 # 小值确保数值稳定
# 创建随机标签(独热编码)
y_batch = np.zeros((batch_size, 10))
for i in range(batch_size):
y_batch[i, np.random.randint(10)] = 1
print("训练开始...")
for epoch in range(5):
loss = model.train_step(x_batch, y_batch, learning_rate=0.01)
print(f"Epoch {epoch+1}, Loss: {loss:.6f}")
print("\n训练完成!")
print("这个例子展示了从数学理论到代码实现的完整过程:")
print("1. 前向传播:每层计算 z = Wx + b")
print("2. 激活函数:应用非线性变换")
print("3. 损失计算:交叉熵损失(Softmax + 交叉熵)")
print("4. 反向传播:链式法则逐层计算梯度")
print("5. 参数更新:梯度下降优化")
5.5 数学洞察与实现细节
关键数学点 1:梯度的数值验证
在实现反向传播时,可以使用数值梯度检验验证数学推导的正确性:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
def numerical_gradient(f, x, h=1e-5):
"""计算数值梯度(用于验证)"""
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'])
while not it.finished:
idx = it.multi_index
old_value = x[idx]
# f(x + h)
x[idx] = old_value + h
fxh_pos = f(x)
# f(x - h)
x[idx] = old_value - h
fxh_neg = f(x)
# 中心差分
grad[idx] = (fxh_pos - fxh_neg) / (2 * h)
x[idx] = old_value
it.iternext()
return grad
def check_gradient(layer, x, dL_dout):
"""验证反向传播的梯度是否正确"""
# 计算解析梯度(通过反向传播)
analytical_grad = layer.backward(dL_dout)
# 计算数值梯度
def loss_fn(W):
layer.W = W
return np.sum(layer.forward(x))
numerical_grad = numerical_gradient(loss_fn, layer.W.copy())
# 比较
rel_error = np.linalg.norm(analytical_grad - numerical_grad) / (
np.linalg.norm(analytical_grad) + np.linalg.norm(numerical_grad)
)
print(f"相对误差: {rel_error:.2e}")
if rel_error < 1e-5:
print("✓ 梯度检验通过!")
else:
print("✗ 梯度检验失败!需要检查实现。")
关键数学点 2:学习率的自适应
在实际应用中,固定学习率往往不够理想。Adam 优化器中的自适应学习率:
\[\alpha_t = \alpha \cdot \frac{\sqrt{1-\beta_2^t}}{1-\beta_1^t} \cdot \frac{1}{\sqrt{\hat{v}_t} + \epsilon}\]这个公式体现了深层的数学:
- 分子中的 $\sqrt{1-\beta_2^t}$ 随着时间衰减,相当于学习率预热
- $\frac{1}{\sqrt{\hat{v}_t}}$ 提供了参数特定的自适应缩放
关键数学点 3:批量归一化的数学本质
批量归一化在每一层的输入进行标准化:
\[\tilde{x}_i = \frac{x_i - \mathbb{E}[x_i]}{\sqrt{\text{Var}[x_i] + \epsilon}}\]然后学习缩放和平移参数 $\gamma$ 和 $\beta$:
\[y_i = \gamma \tilde{x}_i + \beta\]数学本质:这改变了损失函数的Hessian矩阵的条件数,使其更接近 1,从而加快收敛。
常见问题与深度洞察
Q1: 为什么梯度下降能收敛到好的解?
答案:这涉及到泛函分析中的深层理论。对于强凸函数,梯度下降保证线性收敛。但神经网络的损失函数通常不是凸的,为什么还能工作呢?
关键洞察:虽然全局非凸,但梯度下降找到的局部最小值通常已经足够好。最近的理论研究表明:
-
高维空间的几何性质:在高维空间中,”坏”的局部最小值很少。大多数临界点都是鞍点,不是局部最小值。
-
损失函数景观(Loss Landscape)的平坦性:神经网络的损失函数虽然非凸,但在找到的最小值附近通常很平坦,这意味着解的泛化能力好。
-
隐含的正则化:随机梯度下降本身具有隐含的正则化效果,使得找到的解泛化能力更强。
Q2: 为什么 ReLU 比 Sigmoid 更有效?
答案:从梯度流的角度:
-
Sigmoid:$\sigma’(x) = \sigma(x)(1-\sigma(x)) \leq 0.25$,导数始终小于 0.25,在深层网络中造成梯度消失。
-
ReLU:$\text{ReLU}’(x) = \begin{cases} 1 & x > 0 \ 0 & x \leq 0 \end{cases}$,导数为 0 或 1,没有衰减。
这从信息论的角度也可以理解:ReLU 通过稀疏激活(大约 50% 的神经元输出 0)减少了信息冗余。
Q3: 为什么需要动量?
答案:从几何角度,梯度下降在”走廊”形的损失函数中振荡剧烈:
1
2
3
4
5
6
7
^ 损失
|
--|--
/ \ 这样的形状会导致
/ \ 陡峭的垂直梯度
/______\____ 平缓的水平梯度
参数
在这样的地形中:
- 如果只用梯度,在垂直方向振荡剧烈
- 加入动量后,垂直方向的振荡相互抵消,而水平方向的效应累积
数学表现:动量相当于给损失函数添加一个虚部,改变其条件数。
Q4: 深度学习中的”暗物质”是什么?
答案:指的是我们还不完全理解的现象:
-
缩放律(Scaling Laws):为什么模型大小、数据量和计算量之间存在幂律关系? \(\text{Loss} \propto \left(\frac{C}{N}\right)^\alpha\)
-
涌现能力(Emergent Abilities):为什么某些能力在模型达到特定大小时突然出现?
-
双重下降(Double Descent):为什么过度参数化的模型反而泛化更好?
这些现象暗示深度学习中还有深层的数学结构等待发现。
总结
深度学习的优雅之处在于其数学的一致性和优美:
| 概念 | 数学基础 | 实际意义 |
|---|---|---|
| 反向传播 | 链式法则 | 高效计算梯度 |
| 梯度下降 | 一阶泰勒展开 | 参数优化 |
| 动量 | 低通滤波 | 加速收敛 |
| Adam | 适应性矩估计 | 自适应学习率 |
| 交叉熵 | KL 散度 | 概率匹配 |
| 正则化 | 贝叶斯先验 | 防止过拟合 |
| 批量归一化 | Hessian 调理 | 加速训练 |
参考资源
- 经典教科书:《Deep Learning》(Goodfellow et al., 2016)
- 优化理论:Boyd & Vandenberghe, “Convex Optimization”
- 信息论基础:Cover & Thomas, “Elements of Information Theory”
- 现代研究:Arpit et al., “Why Does Batch Normalization Help Optimization?”
附录:代码运行说明
上述代码可以直接运行,会输出训练过程中的损失值下降情况。关键的学习点:
- 逐元素操作:理解每个操作的形状变化
- 链式法则的递归:梯度如何从输出逐层反向传播
- 参数更新:梯度如何转化为参数改进
- 数值稳定性:Softmax 中减去最大值防止溢出