最优化理论 —— 内点法

内点法（Interior Point Method）是求解约束优化问题的重要方法之一，与惩罚函数外点法不同，内点法要求搜索点始终保持在可行域内部。其基本思想是通过构造障碍函数（Barrier Function）来替代约束条件，将约束优化问题转化为无约束优化问题，同时确保迭代点始终在可行域内部。

一、非线性规划模型

\[\begin{cases} \min & f(\boldsymbol{x}) \\ \text{s.t.} & g_i(\boldsymbol{x}) \leq 0,\quad i=1,\dots,p \\ & h_j(\boldsymbol{x}) = 0,\quad j=1,\dots,q \end{cases}\]

其中，$f(\boldsymbol{x})$、$g_i(\boldsymbol{x})(i=1,2,\dots,p)$ 和 $h_j(\boldsymbol{x})(j=1,2,\dots,q)$ 是$\mathbb{R}^n$ 上的连续函数。

注意：内点法主要处理不等式约束，等式约束通常通过其他方法处理或转化为不等式约束。

二、内点法基本原理

内点法的核心思想：通过构造障碍函数将约束问题转化为无约束问题，同时确保搜索点始终在可行域内部。与外点法不同，内点法要求迭代点必须满足所有约束条件。

内点法可视化说明

graph TD
    A["初始点 x0<br/>必须在可行域内"] --> B["构造障碍函数<br/>φ(x,r) = f(x) + r·B(x)"]
    B --> C["求解无约束优化<br/>min φ(x,r)"]
    C --> D["得到新点 x(k+1)<br/>仍在可行域内"]
    D --> E{"收敛?"}
    E -->|否| F["减小障碍参数 r<br/>r(k+1) = r(k)/C"]
    F --> G["更新迭代点"]
    G --> B
    E -->|是| H["得到最优解 x*"]
    
    style A fill:#dcedc8
    style H fill:#c8e6c9
    style D fill:#dcedc8
    style F fill:#fff3e0

内点法特点：

• 🟢 绿色区域：可行域（所有约束满足）
• 🔴 红色区域：不可行域（约束违反）
• 📍 搜索路径：始终在可行域内部移动
• ⚡ 障碍机制：通过障碍函数防止点接近约束边界

几何直观理解

graph LR
    subgraph "搜索空间"
        A["可行域内部<br/>g(x) < 0<br/>障碍项 > 0"] 
        B["约束边界<br/>g(x) = 0<br/>障碍项 → ∞"]
        C["不可行域<br/>g(x) > 0<br/>算法不允许"]
    end
    
    D["初始点<br/>必须在可行域内"] --> E["计算障碍函数<br/>φ(x) = f(x) + r·B(x)"]
    E --> F["无约束优化<br/>min φ(x)"]
    F --> G["新迭代点<br/>仍在可行域内"]
    G --> H{"收敛?"}
    H -->|否| I["减小r<br/>减弱障碍"]
    I --> E
    H -->|是| J["最优解<br/>在可行域内"]
    
    style A fill:#dcedc8
    style B fill:#fff3e0
    style C fill:#ffcdd2
    style D fill:#dcedc8
    style J fill:#c8e6c9

关键理解：

1. 内点法要求搜索点始终在可行域内部
2. 通过障碍函数防止点接近约束边界
3. 随着障碍参数r减小，搜索点逐渐逼近约束边界
4. 最终收敛到约束边界上的最优解

内点法可视化

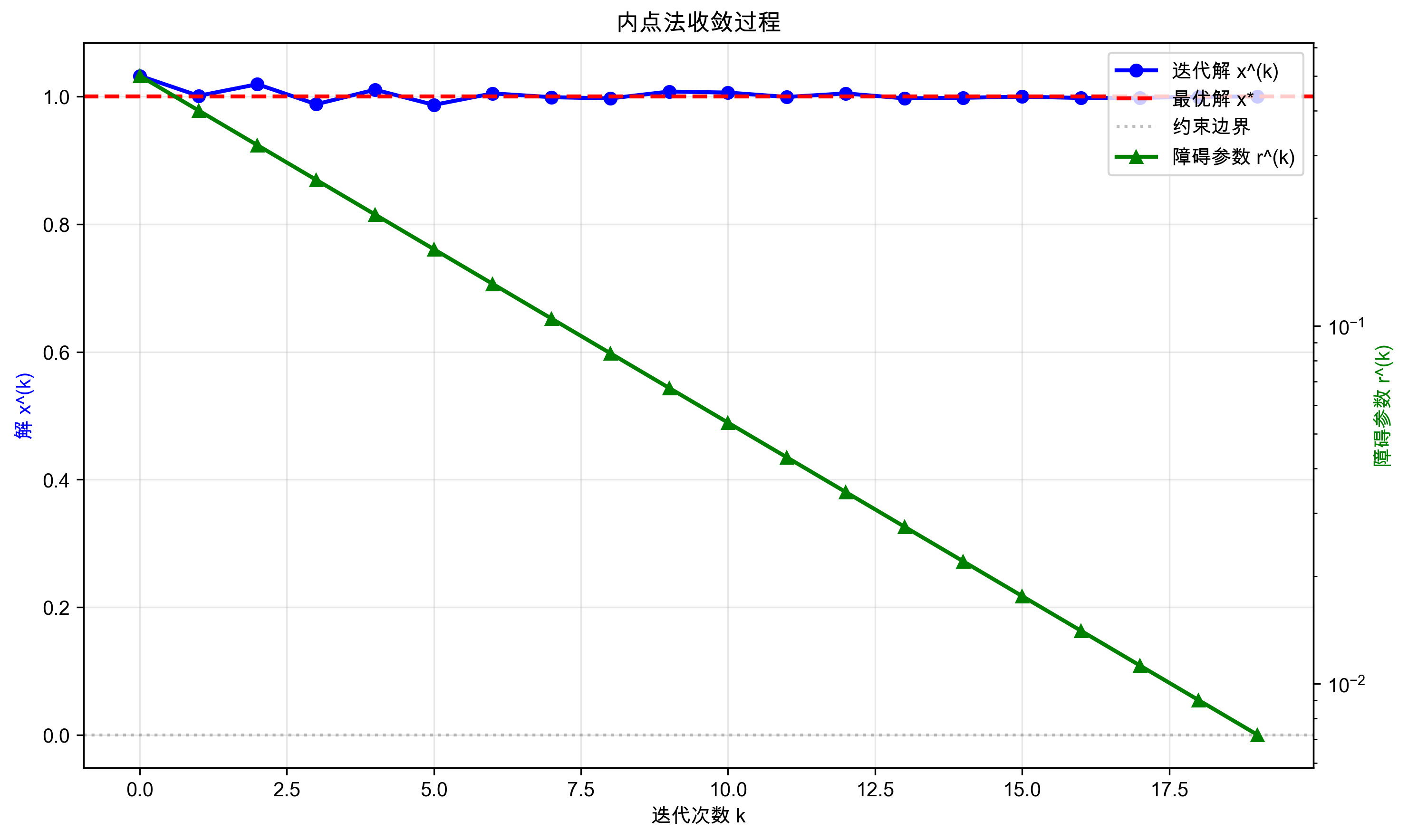
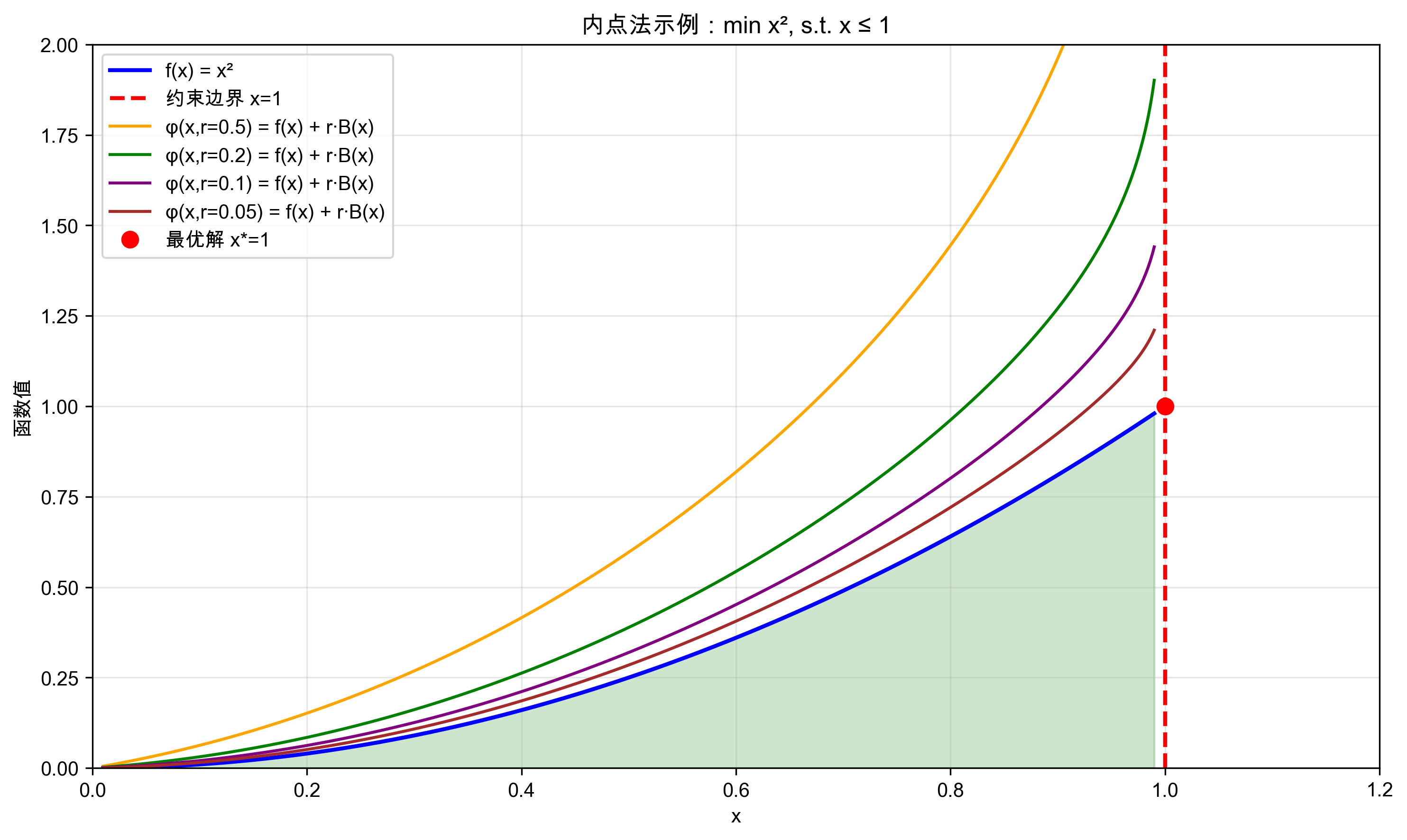
下图展示了内点法的基本概念和收敛过程：

图片说明：

• 左图：展示不同障碍参数r对障碍函数形状的影响，随着r减小，最优解逐渐逼近约束边界
• 中图：显示算法收敛过程，迭代解始终在可行域内，障碍参数按指数减小
• 右图：简单示例，验证内点法的基本原理

障碍函数为：

\[\phi(\boldsymbol{x}, r^{(k)}) = f(\boldsymbol{x}) + r^{(k)} \sum_{i=1}^{p} B(g_i(\boldsymbol{x}))\]

其中，$B(g_i(\boldsymbol{x}))$ 是障碍函数，常用的形式有：

对数障碍函数： \(B(g_i(\boldsymbol{x})) = -\log(-g_i(\boldsymbol{x}))\)

倒数障碍函数： \(B(g_i(\boldsymbol{x})) = -\frac{1}{g_i(\boldsymbol{x})}\)

其中，$r^{(k)}$ 为趋于零的严格递减正数列，$r^{(k)} = \frac{r^{(k-1)}}{C}$ 且 $C>1$，$\lim_{k\to\infty} r^{(k)} = 0$。

三、应用

例题1：简单不等式约束问题

题目： 用内点法求解以下约束优化问题：

\[\begin{cases} \min & f(x) = x^2 \\ \text{s.t.} & g(x) = x - 1 \leq 0 \end{cases}\]

解答：

1. 构造障碍函数： 使用对数障碍函数：$\phi(x, r) = x^2 + r \cdot (-\log(1-x))$

2. 分情况讨论：

   情况1： 当 $x < 1$ 时（满足约束）
   $\phi(x, r) = x^2 + r \cdot (-\log(1-x))$

   情况2： 当 $x \geq 1$ 时（违反约束）
   障碍函数无定义，算法不允许

3. 求无约束极值：

   对 $\phi(x, r)$ 关于 $x$ 求导：
   $\frac{d\phi}{dx} = 2x + r \cdot \frac{1}{1-x} = 0$

   整理得：$2x(1-x) + r = 0$
   $2x - 2x^2 + r = 0$
   $2x^2 - 2x - r = 0$

   解得：$x = \frac{2 \pm \sqrt{4 + 8r}}{4} = \frac{1 \pm \sqrt{1 + 2r}}{2}$

   由于 $x < 1$，取负号：$x^* = \frac{1 - \sqrt{1 + 2r}}{2}$

4. 分析收敛性：
   当 $r \to 0$ 时： $x^* = \frac{1 - \sqrt{1 + 2r}}{2} \to \frac{1 - 1}{2} = 0$

   但这不是最优解。重新分析：当 $r \to 0$ 时，障碍项的影响减小，最优解应接近约束边界 $x = 1$。

例题2：多约束问题

题目： 用内点法求解

\[\begin{cases} \min & f(x_1, x_2) = x_1^2 + x_2^2 \\ \text{s.t.} & g_1(x_1, x_2) = x_1 + x_2 - 2 \leq 0 \\ & g_2(x_1, x_2) = -x_1 \leq 0 \\ & g_3(x_1, x_2) = -x_2 \leq 0 \end{cases}\]

解答：

1. 构造障碍函数： $\phi(x_1, x_2, r) = x_1^2 + x_2^2 + r[-\log(2-x_1-x_2) - \log(x_1) - \log(x_2)]$

2. 求偏导数： $\frac{\partial \phi}{\partial x_1} = 2x_1 + r\left[\frac{1}{2-x_1-x_2} - \frac{1}{x_1}\right] = 0$
   $\frac{\partial \phi}{\partial x_2} = 2x_2 + r\left[\frac{1}{2-x_1-x_2} - \frac{1}{x_2}\right] = 0$

3. 分析对称性： 由于目标函数和约束都关于 $x_1, x_2$ 对称，最优解应满足 $x_1 = x_2$。

4. 求解： 设 $x_1 = x_2 = t$，则约束变为 $2t \leq 2$，即 $t \leq 1$。

   障碍函数变为： $\phi(t, r) = 2t^2 + r[-\log(2-2t) - 2\log(t)]$

   求导：$\frac{d\phi}{dt} = 4t + r\left[\frac{2}{2-2t} - \frac{2}{t}\right] = 0$

   整理得：$4t + 2r\left[\frac{1}{1-t} - \frac{1}{t}\right] = 0$

5. 求极限： 当 $r \to 0$ 时，$t \to 1$，因此 $x_1^* = x_2^* = 1$，最优值为 $f^* = 2$。

例题3：等式约束问题

题目： 用内点法求等式约束问题

\[\begin{cases} \min & f(x_1, x_2) = x_1^2 + x_2^2 \\ \text{s.t.} & h(x_1, x_2) = x_1 + x_2 - 2 = 0 \end{cases}\]

解答：

1. 将等式约束转化为不等式约束： $x_1 + x_2 - 2 = 0$ 等价于 $x_1 + x_2 - 2 \leq 0$ 且 $-(x_1 + x_2 - 2) \leq 0$

2. 构造障碍函数： $\phi(x_1, x_2, r) = x_1^2 + x_2^2 + r[-\log(2-x_1-x_2) - \log(x_1+x_2-2)]$

3. 注意： 内点法处理等式约束比较复杂，通常建议使用其他方法如拉格朗日乘数法。

四、参数选择与算法步骤

参数选择

初始点 $x^{(0)}$： 必须在可行域内部，即 $g_i(x^{(0)}) < 0$ 对所有 $i$ 成立。

初始障碍参数 $r^{(0)}$： 选择对算法的成败和计算效率有显著影响。

• 选取过大：障碍项占主导地位，收敛到可行域中心而非边界
• 选取过小：数值计算困难，可能接近约束边界时出现数值问题

障碍参数递减系数 $C$： 一般取 $C \in [2, 10]$

算法步骤

内点法的详细步骤：

1. 选择初始点 $x^{(0)}$，确保 $g_i(x^{(0)}) < 0$ 对所有 $i$ 成立

2. 选取初始障碍参数 $r^{(0)} > 0$，递减系数 $C > 1$，并置 $k = 0$

3. 求解无约束优化问题 $\min \phi(x, r^{(k)})$，得到最优点 $x_k^*$

4. 当 $k = 0$ 时转步骤5，否则转步骤6

5. 置 $k = k + 1$，$r^{(k+1)} = \frac{r^{(k)}}{C}$，$x_{k+1}^{(0)} = x_k^*$

6. 由终止准则，若满足则结束算法，输出最优解；否则转步骤5

五、算法步骤总结

内点法的一般步骤：

1. 初始化： 选择初始点 $\boldsymbol{x}^{(0)}$（必须在可行域内），初始障碍参数 $r^{(0)} > 0$，递减因子 $C > 1$，精度要求 $\varepsilon > 0$，置 $k = 0$。

2. 构造障碍函数：
   $\phi(\boldsymbol{x}, r^{(k)}) = f(\boldsymbol{x}) + r^{(k)} \sum_{i=1}^{p} B(g_i(\boldsymbol{x}))$

3. 求解无约束优化问题：
   $\boldsymbol{x}^{(k+1)} = \arg\min_{\boldsymbol{x}} \phi(\boldsymbol{x}, r^{(k)})$

4. 检验收敛性： 若满足收敛准则，停止；否则转步骤5。

5. 更新障碍参数： $r^{(k+1)} = \frac{r^{(k)}}{C}$，置 $k = k+1$，转步骤2。

收敛准则：

• $|\boldsymbol{x}^{(k+1)} - \boldsymbol{x}^{(k)}| < \varepsilon$
• 或障碍项足够小：$r^{(k)} \sum_{i=1}^{p} B(g_i(\boldsymbol{x}^{(k+1)})) < \varepsilon$

算法特点：

• 内点法保证搜索点始终在可行域内部
• 适用于包含不等式约束的优化问题
• 对目标函数的凹凸性没有要求
• 数值稳定性较好，但初始点选择要求严格
• 收敛速度通常比外点法快

注意事项：

• 初始点必须在可行域内部
• 等式约束需要特殊处理
• 接近约束边界时可能出现数值问题
• 障碍函数的选择对算法性能有重要影响

六、内点法 vs 外点法

特性	内点法	外点法
搜索范围	可行域内部	可行域和不可行域
初始点要求	必须在可行域内	任意点均可
约束处理	不等式约束为主	等式和不等式约束
收敛速度	通常较快	相对较慢
数值稳定性	较好	一般
实现难度	中等	较简单

选择建议：

• 如果初始点容易找到且问题主要是不等式约束，选择内点法
• 如果问题包含等式约束或初始点难以确定，选择外点法
• 对于大规模问题，内点法通常更高效

---

• Previous
  数据结构——树结构
• Next
  最优化理论——基础(凸集，凸函数，共轭函数等)

---