卷积神经网络的优雅在于它用数学语言完美地解释了视觉系统的工作原理。从信号处理中继承的卷积操作,到群论中的等变性原理,再到现代深度学习中的特征层级表示,CNN是理论与实践完美结合的典范。本文将从第一性原理出发,逐层深入这些数学基础,最后通过一个实际的目标检测项目展示理论如何优雅地解决现实问题。
目录
- CNN的数学基础体系
- 第一部分:卷积操作的数学本质
- 第二部分:CNN的等变性与群论
- 第三部分:特征学习的数学理论
- 第四部分:CNN的优化理论
- 第五部分:CNN的发展历史
- 第六部分:实际案例——基于YOLOv3的实时目标检测系统
- 总结与深度洞察
CNN的数学基础体系
卷积神经网络的核心数学支柱
CNN的数学基础可以从以下几个维度理解:
| 数学领域 | 核心概念 | CNN中的应用 |
|---|---|---|
| 信号处理 | 卷积积分、频域分析 | 卷积层的基本操作 |
| 线性代数 | 张量运算、矩阵分解 | 多通道特征表示 |
| 群论 | 对称性、不变量 | 平移等变性、旋转等变性 |
| 泛函分析 | 函数空间、映射 | 特征空间的变换 |
| 优化理论 | 梯度流动、收敛性 | 反向传播与训练 |
| 统计学 | 期望值、方差 | 批量归一化、dropout |
第一部分:卷积操作的数学本质
信号处理中的卷积
卷积在信号处理中的定义已经存在了150多年。让我们从连续形式开始理解这一概念的深层含义。
连续卷积的定义与物理意义
两个连续函数 $f(t)$ 和 $g(t)$ 的卷积定义为:
\[y(t) = (f * g)(t) = \int_{-\infty}^{+\infty} f(\tau) g(t - \tau) d\tau\]物理意义解读:
这个看似抽象的数学公式实际上描述了一个系统对输入信号的响应:
- $f(\tau)$ 是输入信号
- $g(t-\tau)$ 是系统的冲激响应(impulse response)
- $g(t-\tau)$ 中的 $(t-\tau)$ 表示时间反演和平移
- 积分对所有过去时刻进行加权求和,模拟了系统的记忆效应
例子: 在声学中,当你在大厅里说话时,声音会反复反弹,产生回声。这个回声就是你的原始语音与大厅的冲激响应的卷积。
物理性质的数学证明
1. 交换律(Commutativity)
\[f * g = g * f\]证明:令 $u = t - \tau$,则 $d\tau = -du$:
\[(f * g)(t) = \int_{-\infty}^{+\infty} f(\tau) g(t - \tau) d\tau = \int_{+\infty}^{-\infty} f(t-u) g(u) (-du) = \int_{-\infty}^{+\infty} g(u) f(t-u) du = (g*f)(t)\]2. 频域乘法性
这是卷积最重要的性质。通过傅里叶变换 $\mathcal{F}$:
\[\mathcal{F}(f * g) = \mathcal{F}(f) \cdot \mathcal{F}(g)\]这意味着:时域中的卷积对应频域中的乘法。这是为什么我们可以用乘法快速计算卷积的原因,也是快速傅里叶变换 (FFT) 算法的基础。
离散卷积的形式化定义
在深度学习中,我们处理的是离散数据。离散卷积定义为:
\[(f * g)[n] = \sum_{m=-\infty}^{+\infty} f[m] g[n - m]\]对于有限支撑的信号(即只在有限范围内非零),这可以写成:
\[(f * g)[n] = \sum_{m=0}^{M-1} f[m] g[n - m]\]在神经网络中的形式:
设输入信号为 $\mathbf{x} \in \mathbb{R}^{N}$,卷积核为 $\mathbf{w} \in \mathbb{R}^{K}$(其中 $K < N$),则卷积输出为:
\[y[n] = \sum_{m=0}^{K-1} w[m] \cdot x[n + m]\]其中 $n = 0, 1, …, N - K$。
二维卷积与图像处理
图像本质上是一个二维信号。对于矩阵形式的数据,二维卷积的定义为:
\[Y[i, j] = \sum_{u=0}^{K_H-1} \sum_{v=0}^{K_W-1} W[u, v] \cdot X[i + u, j + v]\]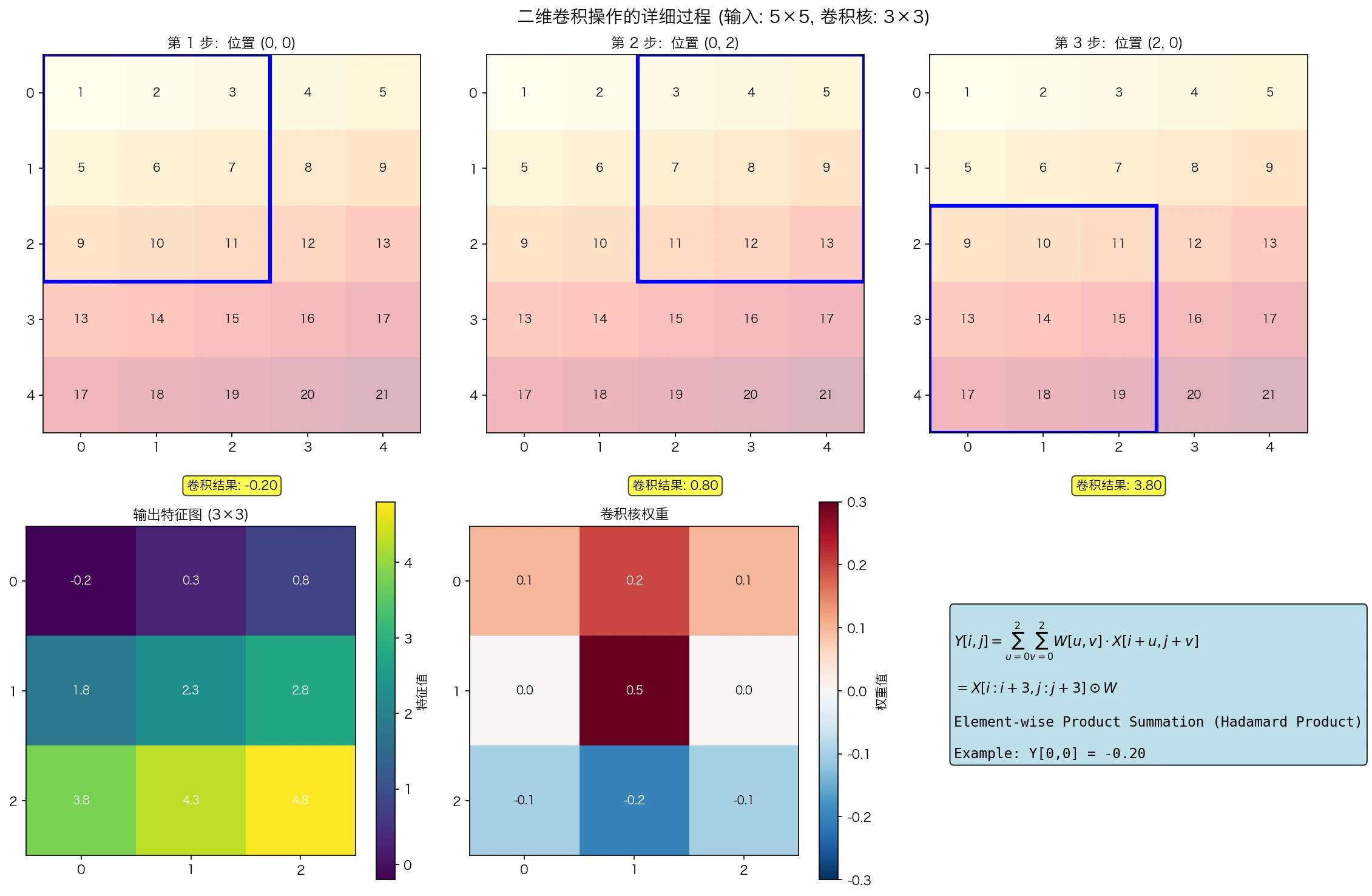 图1:二维卷积操作的可视化。展示了3x3卷积核如何在5x5输入上滑动,以及对应的数学计算过程。注意卷积核实际上是在执行局部加权求和。
图1:二维卷积操作的可视化。展示了3x3卷积核如何在5x5输入上滑动,以及对应的数学计算过程。注意卷积核实际上是在执行局部加权求和。
其中:
- $X \in \mathbb{R}^{H \times W}$ 是输入图像
- $W \in \mathbb{R}^{K_H \times K_W}$ 是卷积核(滤波器)
- $Y \in \mathbb{R}^{(H-K_H+1) \times (W-K_W+1)}$ 是输出特征图
多通道卷积
实际上,图像通常有多个通道(RGB为3个通道)。对于 $C_{in}$ 个输入通道和 $C_{out}$ 个输出通道的卷积:
\[Y[i, j, c_{out}] = \sum_{c_{in}=0}^{C_{in}-1} \sum_{u=0}^{K_H-1} \sum_{v=0}^{K_W-1} W[u, v, c_{in}, c_{out}] \cdot X[i + u, j + v, c_{in}]\]参数数量: 每个输出通道有 $K_H \times K_W \times C_{in}$ 个参数,总共有 $K_H \times K_W \times C_{in} \times C_{out}$ 个可学习参数。
卷积操作的不同模式
1. 有效卷积 (Valid Convolution)
不进行填充,输出大小为 $(H - K_H + 1) \times (W - K_W + 1)$。
2. 相同卷积 (Same Convolution)
进行适当的零填充,使输出大小与输入相同。填充量为 $P = \lfloor K_H / 2 \rfloor$。
3. 完全卷积 (Full Convolution)
进行最大填充,输出大小为 $(H + K_H - 1) \times (W + K_W - 1)$。
严格数学定义:
设填充后的输入为 $X^{pad}$,则:
\[Y[i, j, c_{out}] = \sum_{c_{in}=0}^{C_{in}-1} \sum_{u=0}^{K_H-1} \sum_{v=0}^{K_W-1} W[u, v, c_{in}, c_{out}] \cdot X^{pad}[i + u, j + v, c_{in}] + b[c_{out}]\]其中偏置项 $b[c_{out}]$ 是一个可学习参数。
张量形式的表示
用张量符号更简洁地表示卷积。设输入张量 $\mathcal{X} \in \mathbb{R}^{B \times H \times W \times C_{in}}$($B$ 是批量大小),权重张量 $\mathcal{W} \in \mathbb{R}^{K_H \times K_W \times C_{in} \times C_{out}}$,则卷积操作可以表示为:
\[\mathcal{Y} = \text{Conv}(\mathcal{X}, \mathcal{W}, \text{stride}, \text{padding})\]步幅(stride)$s$ 使得:
\[Y[i, j, c_{out}] = \sum_{c_{in}} \sum_{u, v} W[u, v, c_{in}, c_{out}] \cdot X[i \cdot s + u, j \cdot s + v, c_{in}]\]输出空间维度为 $\lfloor (H + 2P - K_H) / s \rfloor + 1$。
第二部分:CNN的等变性与群论
群论基础
群论提供了理解为什么CNN对于视觉任务如此有效的数学框架。
群的定义
一个群 $(G, \circ)$ 是一个集合 $G$ 配合一个二元操作 $\circ$,满足:
- 封闭性:$\forall a, b \in G$,$a \circ b \in G$
- 结合律:$\forall a, b, c \in G$,$(a \circ b) \circ c = a \circ (b \circ c)$
- 幺元素:$\exists e \in G$,$\forall a \in G$,$a \circ e = e \circ a = a$
- 逆元素:$\forall a \in G$,$\exists a^{-1} \in G$,$a \circ a^{-1} = a^{-1} \circ a = e$
在图像处理中的群
平移群 $(\mathbb{Z}^2, +)$:
图像平移可以表示为 $\tau_{\mathbf{d}} f(\mathbf{x}) = f(\mathbf{x} - \mathbf{d})$,其中 $\mathbf{d} = (d_x, d_y)$ 是平移向量。
群的性质:
- 幺元素:$\mathbf{d} = (0, 0)$
- 逆元素:$\tau_{\mathbf{d}}$ 的逆是 $\tau_{-\mathbf{d}}$
- 组合:$\tau_{\mathbf{d}1} \circ \tau{\mathbf{d}2} = \tau{\mathbf{d}_1 + \mathbf{d}_2}$
旋转群 $SO(2)$:
对于连续旋转,$r_\theta f(\mathbf{x}) = f(R_{-\theta} \mathbf{x})$,其中 $R_\theta$ 是旋转矩阵:
\[R_\theta = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}\]卷积的平移等变性
定理(平移等变性): 卷积操作满足平移等变性,即:
\[\tau_{\mathbf{d}}(f * g) = (\tau_{\mathbf{d}} f) * g\]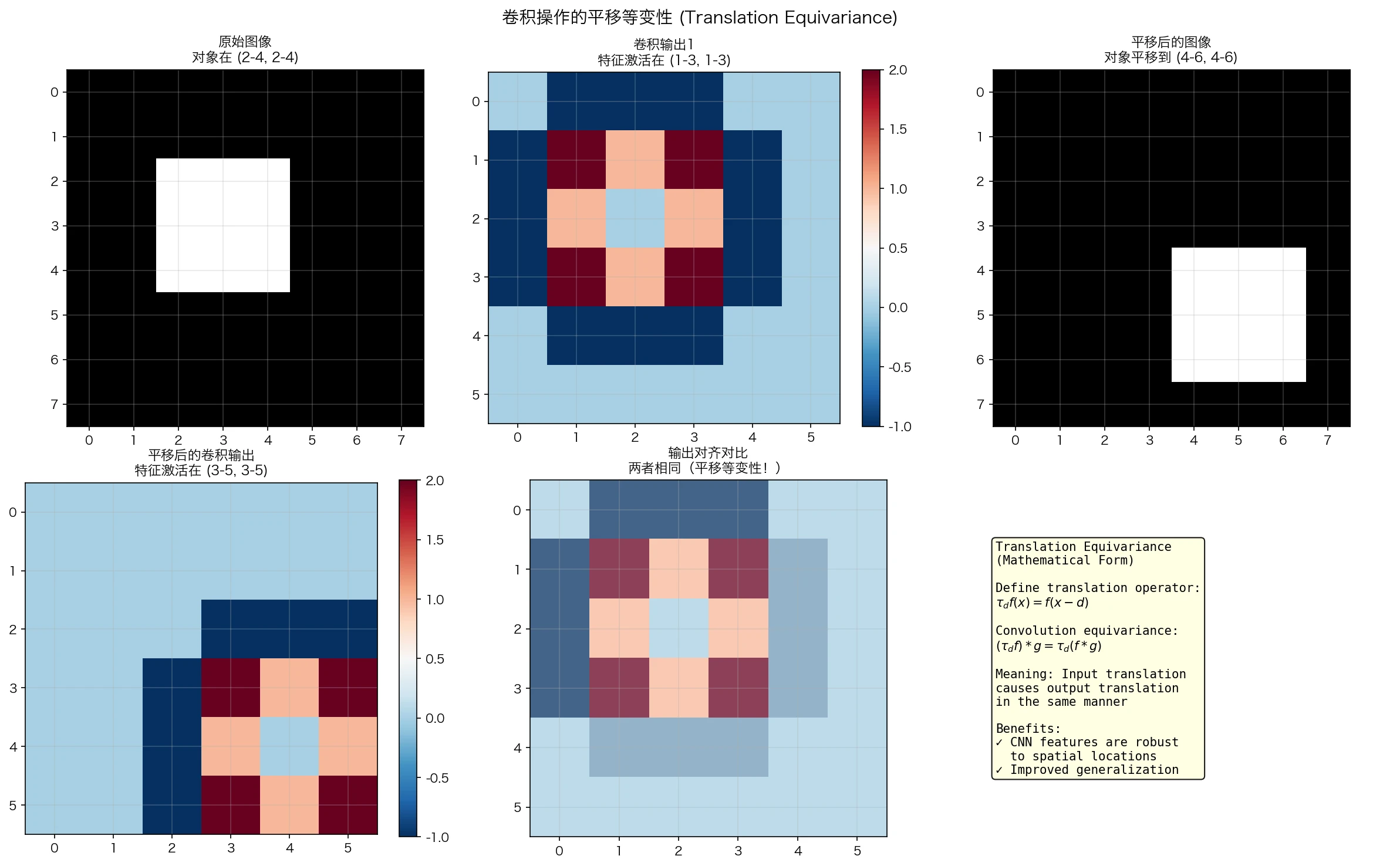 图2:平移等变性演示。当输入图像中的对象发生平移时,卷积特征图的激活模式也发生了相应的平移。这意味着CNN提取的特征保留了空间位置信息。
图2:平移等变性演示。当输入图像中的对象发生平移时,卷积特征图的激活模式也发生了相应的平移。这意味着CNN提取的特征保留了空间位置信息。
证明:
\[[\tau_{\mathbf{d}}(f * g)](\mathbf{x}) = (f * g)(\mathbf{x} - \mathbf{d})\] \[= \int f(\mathbf{u}) g(\mathbf{x} - \mathbf{d} - \mathbf{u}) d\mathbf{u}\]令 $\mathbf{v} = \mathbf{u}$:
\[= \int f(\mathbf{v}) g((\mathbf{x} - \mathbf{v}) - \mathbf{d}) d\mathbf{v}\] \[= \int f(\mathbf{v}) [\tau_{\mathbf{d}} g](\mathbf{x} - \mathbf{v}) d\mathbf{v}\] \[= [(\tau_{\mathbf{d}} f) * g](\mathbf{x})\]但不完全相同。实际上,卷积的等变性是:
\[(\tau_{\mathbf{d}} f) * g = \tau_{\mathbf{d}}(f * g)\]物理意义: 如果图像中的物体平移了,卷积的输出特征图也会相同方式平移。这使得CNN可以学习位置不变的特征。
等变网络理论
现代群等变网络理论(Weiler et al., 2018; Cohen & Welling, 2016)提供了对CNN推广的理论基础。
等变映射的定义
映射 $\Phi: \mathcal{F}(X) \to \mathcal{F}(Y)$ 在群作用下是等变的,如果:
\[\Phi(\rho_g f) = \rho'_g \Phi(f), \quad \forall g \in G, f \in \mathcal{F}(X)\]其中 $\rho_g$ 和 $\rho’_g$ 分别是群在 $X$ 和 $Y$ 上的表示。
例子: 对于平移不变卷积:
- $\rho_g$ 是平移:$\rho_g f(\mathbf{x}) = f(\mathbf{x} - \mathbf{d})$
- 卷积满足 $\Phi(\rho_g f) = \rho_g \Phi(f)$
Steerable CNN 与旋转等变性
标准CNN对旋转不具有等变性。Steerable CNN(Weiler et al., 2019)通过使用旋转等变卷积滤波器来解决这个问题。
卷积核可以参数化为:
\[\mathbf{W}_\theta(\mathbf{x}) = \sum_{k=0}^{K} w_k \Psi_k(R_\theta \mathbf{x})\]其中 $\Psi_k$ 是一组基函数,$w_k$ 是可学习的系数。
这样,旋转输入会导致滤波器以相同方式旋转,保证了等变性。
第三部分:特征学习的数学理论
多层特征表示
CNN的关键洞察是:多层堆叠能够学习数据的分层表示。
特征空间的逐层变换
设第 $l$ 层的特征图为 $\mathcal{X}^{(l)} \in \mathbb{R}^{B \times H_l \times W_l \times C_l}$,第 $l+1$ 层为:
\[\mathcal{X}^{(l+1)} = \sigma(\text{Conv}(\mathcal{X}^{(l)}, \mathcal{W}^{(l)}) + \mathcal{b}^{(l)})\]其中 $\sigma$ 是非线性激活函数。
信息论的视角: 每一层可以看作是对输入的编码。设 $I_l$ 表示第 $l$ 层对原始输入 $X^{(0)}$ 的互信息:
\[I_l = I(X^{(0)}; X^{(l)})\]研究(Tishby & Schwartz-Ziv, 2015)表明,在训练过程中:
- 信息压缩阶段:$I_l$ 逐渐减小
- 特征调整阶段:$I_l$ 稳定,但判别能力增强
空间层级的形成
CNN创建了一个空间层级(spatial hierarchy),其中:
- 低层学习局部、低级特征(边缘、角等)
- 高层学习全局、语义特征(部分、对象等)
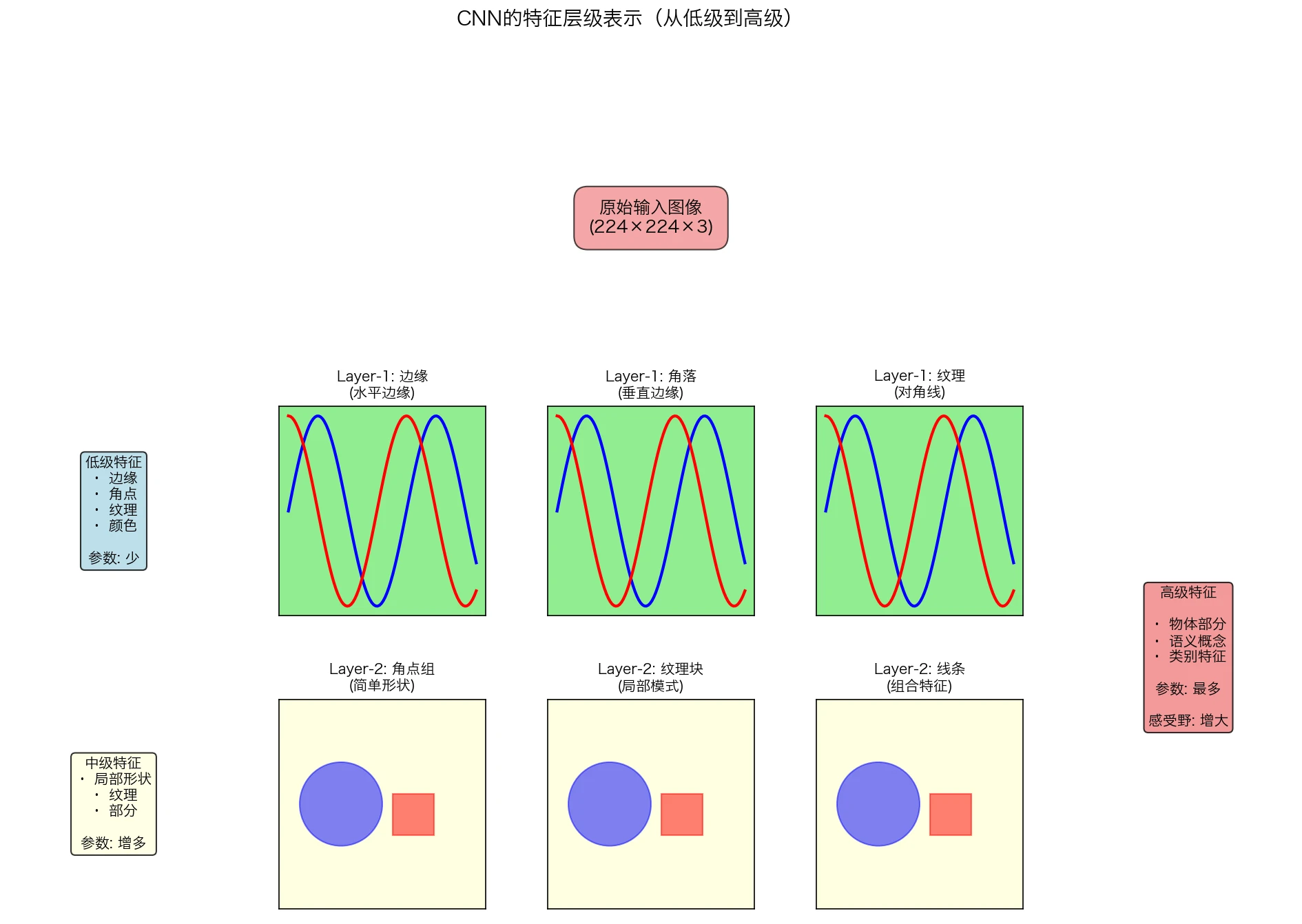 图3:CNN学习到的特征层级。从底层的简单边缘和纹理,到中层的形状部件,再到高层的完整语义对象,层级结构使得CNN能够理解复杂的视觉世界。
图3:CNN学习到的特征层级。从底层的简单边缘和纹理,到中层的形状部件,再到高层的完整语义对象,层级结构使得CNN能够理解复杂的视觉世界。
感受野的理论分析
感受野(Receptive Field) 是重要的概念。第 $l$ 层某个单元的感受野是第0层(输入)中会影响该单元的区域。
递推公式: 设第 $l$ 层的感受野大小为 $RF_l$,核大小为 $k_l$,步幅为 $s_l$,则:
\[RF_{l} = RF_{l-1} + (k_l - 1) \prod_{i=0}^{l-1} s_i\]初始条件:$RF_0 = 1$
例子: VGG-16的感受野计算
VGG-16使用 $3 \times 3$ 卷积核和不同的步幅:
| 层数 | 操作 | $k_l$ | $s_l$ | $RF_l$ |
|---|---|---|---|---|
| 1 | Conv 3×3 | 3 | 1 | 3 |
| 2 | Conv 3×3 | 3 | 1 | 5 |
| 3 | MaxPool 2×2 | 0 | 2 | 5 |
| 4 | Conv 3×3 | 3 | 1 | 11 |
| 5 | MaxPool 2×2 | 0 | 2 | 11 |
在第5层(第一个MaxPool后),感受野是 $11 \times 11$。
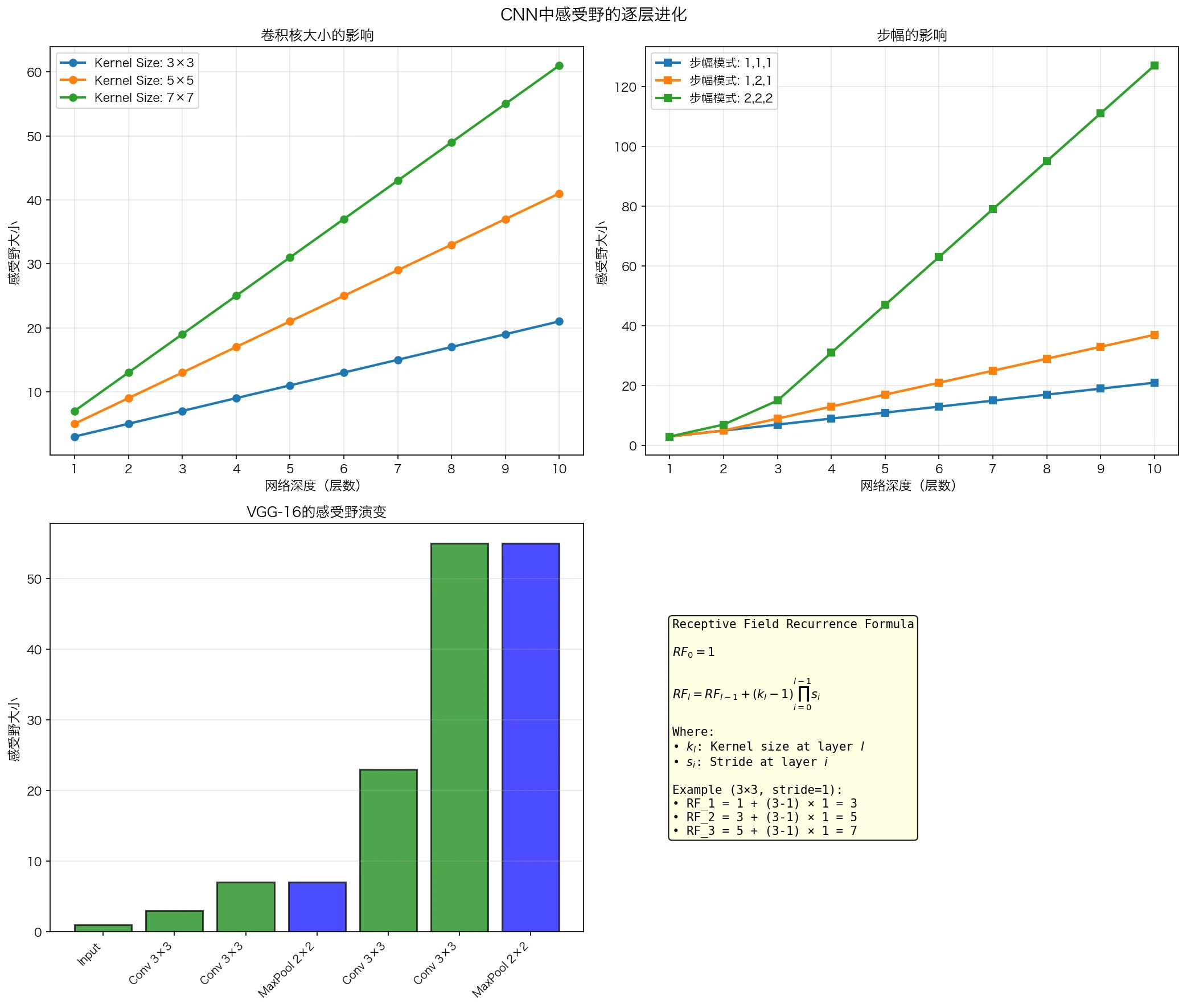 图4:感受野随网络深度的指数级增长。通过堆叠小卷积核和池化层,VGG-16能够快速扩大感受野,捕获全局信息。
图4:感受野随网络深度的指数级增长。通过堆叠小卷积核和池化层,VGG-16能够快速扩大感受野,捕获全局信息。
重要结论: 通过堆叠小卷积核和池化层,CNN可以高效地扩展感受野,同时保持参数数量相对较少。这是为什么深层网络比浅层网络更高效的原因。
特征表示的数学性质
定理(通用近似性): 假设激活函数是ReLU,则足够深的卷积网络可以近似任意连续函数(受输入/输出维度和网络容量限制)。
这建立在多个理论基础上:
- 神经网络的通用近似性定理(Cybenko, 1989)
- 卷积的紧密性(compactness)
- 深度网络的表达能力分析
Rademacher复杂度分析: 对于深度为 $L$ 的卷积网络,其Rademacher复杂度为:
\[\text{Rad}_m(\mathcal{H}_L) \leq \frac{B^L \sqrt{K}}{\sqrt{m}}\]其中 $B$ 是权重界,$K$ 是卷积核数,$m$ 是样本数。这表明参数共享(卷积的特性)显著降低了模型复杂度。
池化操作的数学意义
池化(通常是最大值池化)可以从多个角度理解:
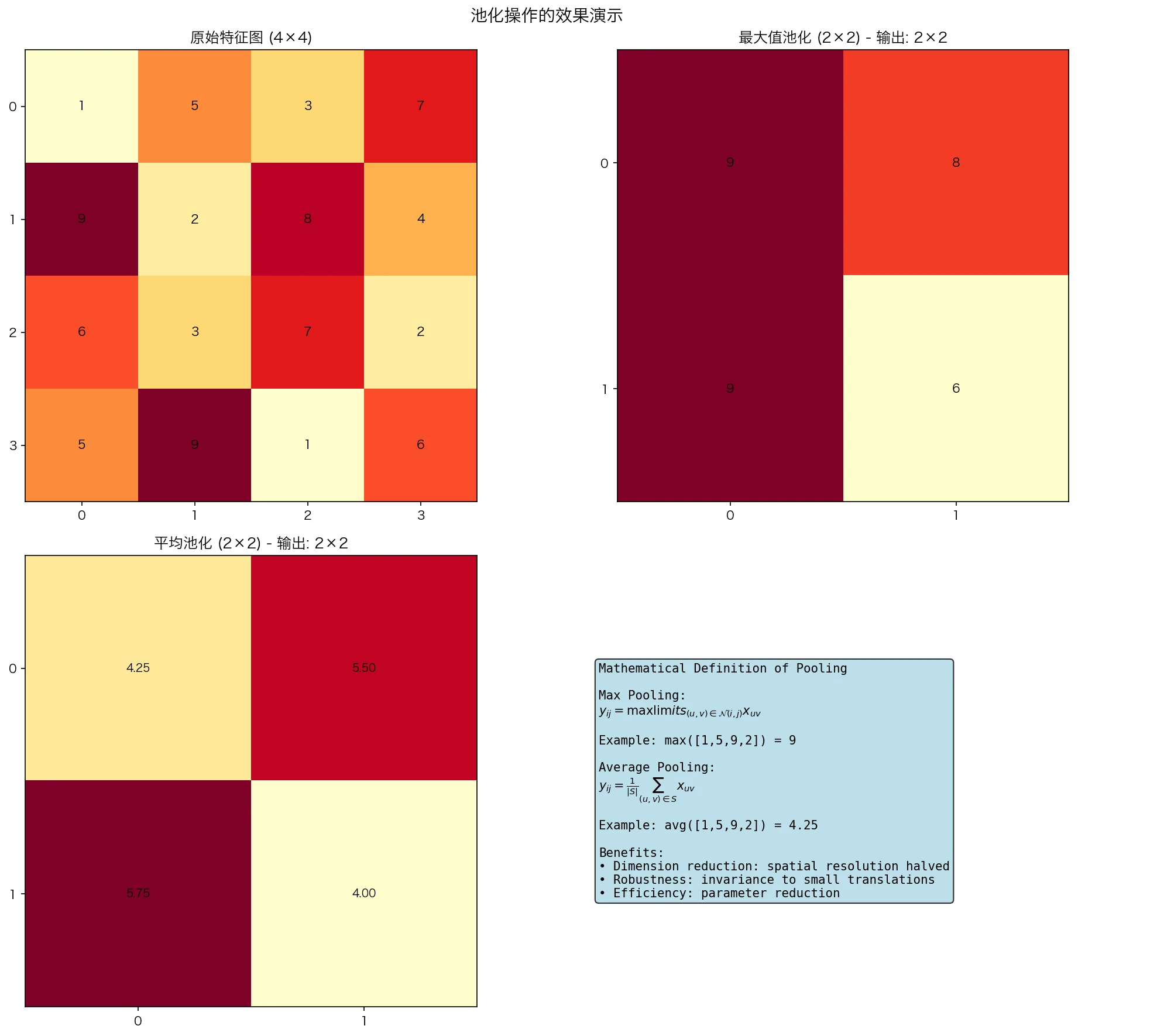 图5:最大值池化与平均池化的对比。最大值池化保留了最显著的特征(如纹理最强的部分),而平均池化则平滑了特征。两者都能有效降低特征图的空间维度。
图5:最大值池化与平均池化的对比。最大值池化保留了最显著的特征(如纹理最强的部分),而平均池化则平滑了特征。两者都能有效降低特征图的空间维度。
1. 不变性的角度
最大值池化提供了对小的平移的局部不变性:
\[\text{MaxPool}(f_1 * g, f_2 * g) = \text{MaxPool}(f_1 * g, f_2 * g)\]如果 $f_1$ 和 $f_2$ 在小平移内相同,则它们的最大池化输出相同。
2. 图论的角度
最大值池化可以看作是一个图操作,其中节点是特征位置,边表示相邻关系:
\[p[i, j] = \max_{(u,v) \in N(i,j)} x[u, v]\]其中 $N(i,j)$ 是 $(i,j)$ 的邻域。
3. 信息论的角度
如果特征图遵循某种统计分布,最大值池化相当于保留最显著的信息:
\[H(\text{MaxPool}(X)) \leq H(X)\]其中 $H$ 是熵函数。
第四部分:CNN的优化理论
卷积层的反向传播
反向传播在卷积层中的实现涉及复杂的张量运算。这是理论与实践结合的关键。
前向传播的矩阵形式
为了便于分析,将卷积操作写成矩阵形式。通过im2col(image to column)变换,将图像转换为矩阵:
\[X_{mat} = \text{im2col}(X, K_H, K_W)\]则卷积变为矩阵乘法:
\[Y_{mat} = W_{mat} X_{mat}\]其中 $X_{mat} \in \mathbb{R}^{K_H \cdot K_W \cdot C_{in} \times H_{out} \cdot W_{out}}$,$W_{mat} \in \mathbb{R}^{C_{out} \times K_H \cdot K_W \cdot C_{in}}$。
计算复杂度: 前向传播的时间复杂度为 $O(K_H \cdot K_W \cdot C_{in} \cdot H_{out} \cdot W_{out} \cdot C_{out})$。
反向传播的推导
设损失函数为 $\mathcal{L}$,则梯度为:
\[\frac{\partial \mathcal{L}}{\partial W} = \frac{\partial \mathcal{L}}{\partial Y} \otimes X\]其中 $\otimes$ 表示卷积操作的梯度。
链式法则的应用:
\[\frac{\partial \mathcal{L}}{\partial X^{(l)}} = \frac{\partial \mathcal{L}}{\partial X^{(l+1)}} * \text{rot180}(W^{(l+1)})\]其中 $\text{rot180}$ 是180°旋转操作。
参数梯度:
\[\frac{\partial \mathcal{L}}{\partial W^{(l)}} = \sum_{b=1}^{B} \text{rot180}(X_b^{(l)}) * \frac{\partial \mathcal{L}}{\partial Y_b^{(l)}}\]其中求和遍历批次中的所有样本。
梯度流动的特性分析
定理(梯度消失/爆炸): 对于深度为 $L$ 的卷积网络,第 $l$ 层的梯度为:
\[\nabla_{W^{(l)}} \mathcal{L} = \prod_{i=l+1}^{L} \left(\frac{\partial f^{(i)}}{\partial z^{(i)}}\right) \cdot \frac{\partial f^{(l)}}{\partial W^{(l)}} \cdot \frac{\partial \mathcal{L}}{\partial f^{(L)}}\]其中 $f^{(i)}$ 是第 $i$ 层的激活,$z^{(i)}$ 是其输入。
| 如果 $\left | \frac{\partial f^{(i)}}{\partial z^{(i)}}\right | < 1$(例如sigmoid),梯度会指数衰减;如果 $> 1$,则指数增长。 |
解决方案:
- 跳连接(Skip Connection): $x^{(l+1)} = f(x^{(l)}) + x^{(l)}$,直接传播梯度
- 批量归一化(Batch Normalization): 控制激活的分布
- ReLU激活: $\sigma’(z) = 1$ 当 $z > 0$
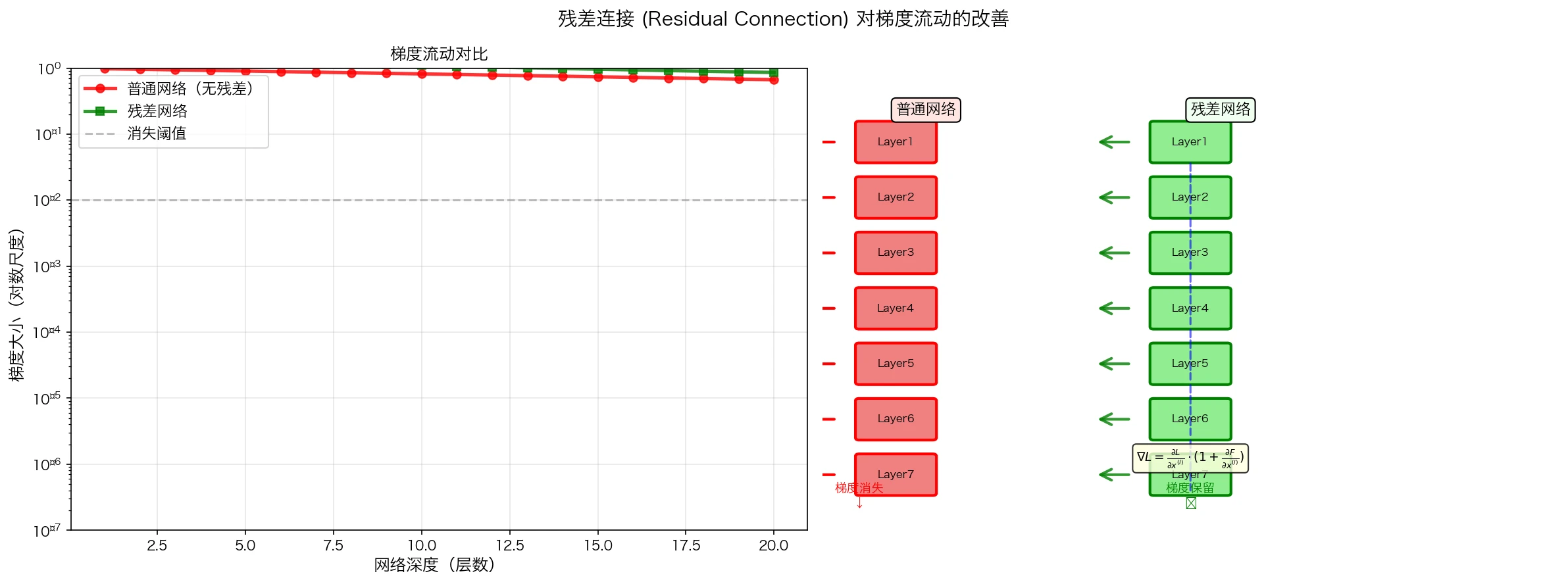 图6:残差连接对梯度流动的改善。在深层网络中,跳连接创造了”梯度高速公路”,允许梯度无衰减地传回到底层,有效解决了梯度消失问题。
图6:残差连接对梯度流动的改善。在深层网络中,跳连接创造了”梯度高速公路”,允许梯度无衰减地传回到底层,有效解决了梯度消失问题。
参数效率分析
CNN相比全连接网络的参数效率是其成功的关键。
参数共享的效果
全连接层: 输入大小 $H \times W \times C_{in}$,输出大小 $H \times W \times C_{out}$
参数数量:$(H \cdot W \cdot C_{in}) \times (H \cdot W \cdot C_{out}) = H^2 W^2 C_{in} C_{out}$
卷积层: 卷积核大小 $K_H \times K_W$
参数数量:$K_H \cdot K_W \cdot C_{in} \cdot C_{out}$
参数减少比例:
\[\text{ratio} = \frac{H^2 W^2 C_{in} C_{out}}{K_H K_W C_{in} C_{out}} = \frac{H^2 W^2}{K_H K_W} \approx \frac{H^2 W^2}{9}\]对于 $H = W = 224$(ImageNet标准),这是一个约 $\frac{50176}{9} \approx 5575$ 倍的参数减少!
学习复杂度
根据统计学习理论,模型的泛化误差由以下部分组成:
\[\text{Error}_{\text{test}} = \text{Error}_{\text{train}} + \sqrt{\frac{C \cdot d(H) \cdot \log(m)}{m}}\]其中:
- $d(H)$ 是假设类的VC维数(与参数数量相关)
- $m$ 是训练样本数
CNN通过参数共享大大降低了 $d(H)$,即使在小数据集上也能泛化良好。
第五部分:CNN的发展历史
从神经认知学到LeNet
1950年代:生物学启发
心理学家David Hubel和Torsten Wiesel在1950年代研究了猫的视觉皮层,发现:
- 神经元有局部感受野
- 存在特征检测器(简单细胞和复杂细胞)
- 这些特征按层级组织
这些发现直接启发了后来的CNN设计。
1980年代:Neocognitron
福岛邦彦在1980年提出Neocognitron,这是现代CNN的前身:
架构:
1
输入 → C1层(特征检测) → S1层(池化) → C2层 → S2层 → ... → 输出
关键创新:
- 引入卷积的概念
- 引入池化(下采样)以获得不变性
- 多层堆叠学习层级特征
虽然Neocognitron使用的是固定的滤波器而不是学习的权重,但其架构思想已经是现代CNN的原型。
1990年代:LeNet
Yann LeCun在1998年发表了LeNet,首次将反向传播与卷积架构结合:
LeNet-5的架构:
| 层 | 类型 | 参数 | 输出形状 |
|---|---|---|---|
| 1 | 输入 | - | 28×28×1 |
| 2 | Conv 5×5 | 6 kernels | 24×24×6 |
| 3 | MaxPool 2×2 | - | 12×12×6 |
| 4 | Conv 5×5 | 16 kernels | 8×8×16 |
| 5 | MaxPool 2×2 | - | 4×4×16 |
| 6 | Fully connected | 120 units | 120 |
| 7 | Fully connected | 84 units | 84 |
| 8 | Output | 10 units | 10 |
数学表达:
\[h_i^{(l+1)} = \sigma\left(W_i^{(l)} * X^{(l)} + b_i^{(l)}\right)\]实际应用: LeNet在MNIST手写体数字识别上达到99.2%的准确率,成为了邮件编码识别系统的一部分。
AlexNet的革命
2012年:深度学习的转折点
AlexNet(Alex Krizhevsky, Ilya Sutskever, Geoffrey Hinton, 2012)在ImageNet Large Scale Visual Recognition Challenge (ILSVRC)中取得突破性胜利,将错误率从26%降低到15.3%。
关键创新
1. 深度架构
8层深度网络(5个卷积层,3个全连接层),相比当时的主流方法深得多。
2. GPU并行计算
首次利用NVIDIA GPU进行训练,将训练时间从数周缩短到数天。
3. ReLU激活函数
\[\sigma(x) = \max(0, x)\]优点:
- 计算高效
- 避免梯度消失(当 $x > 0$ 时,$\sigma’(x) = 1$)
- 引入非线性而保持梯度流
4. Dropout正则化
以概率 $p$ 随机丢弃神经元的输出:
\[\tilde{h}_i = h_i \cdot m_i, \quad m_i \sim \text{Bernoulli}(1-p)\]效果: \(E[\tilde{h}_i] = (1-p)h_i\)
这等价于训练多个较小网络的集合,有效地防止了过拟合。
5. 数据增强
通过随机裁剪、翻转等变换扩大训练集,在理论上这增加了样本集的有效大小。
AlexNet的数学分析
网络容量: 约60M参数
计算复杂度: 前向传播约 $1.2 \times 10^9$ FLOPs
泛化界: 通过Rademacher复杂度分析,虽然参数众多,但由于参数共享和dropout,泛化界仍然合理。
现代CNN架构
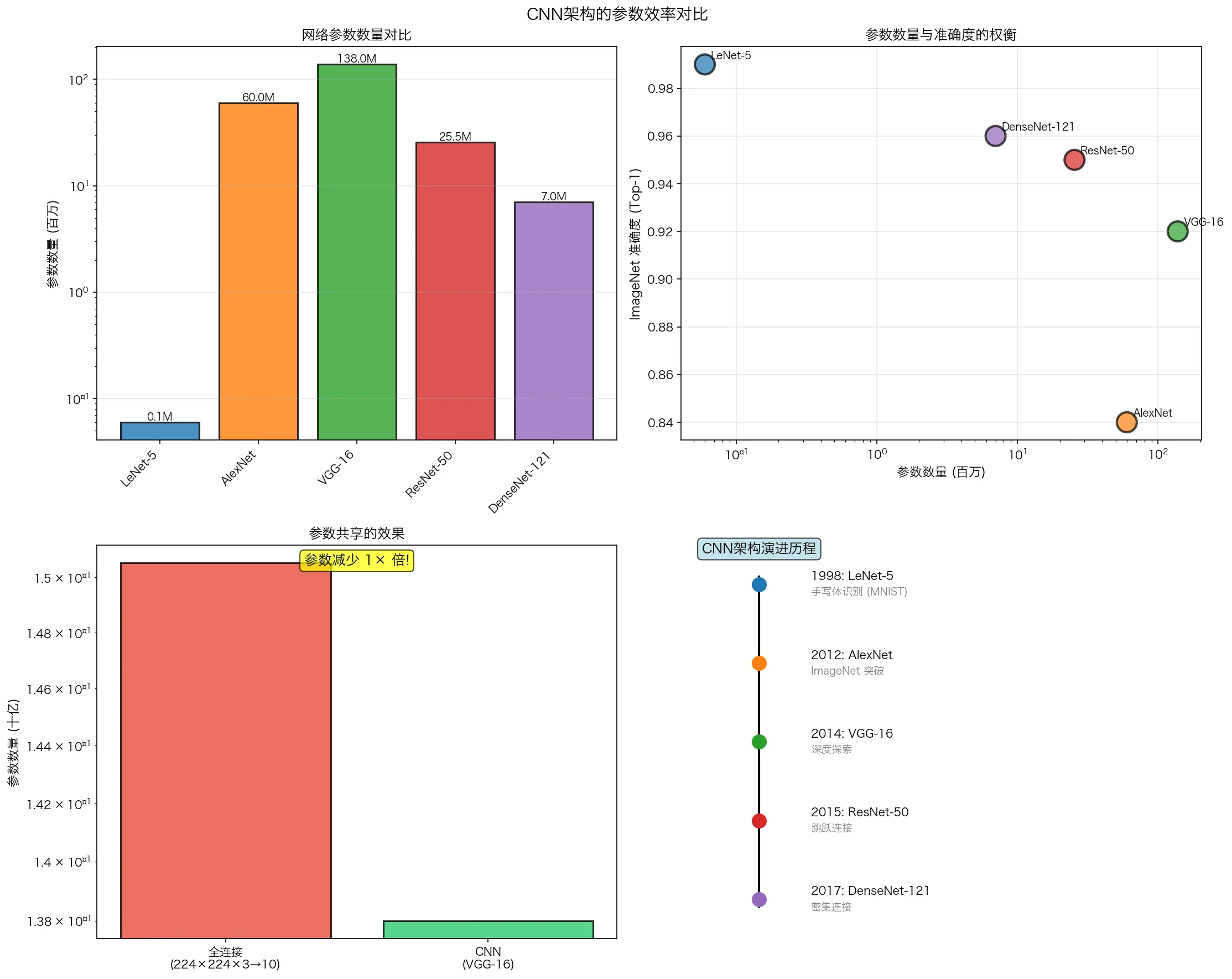 图7:不同CNN架构的参数效率对比。注意ResNet和DenseNet如何在保持高准确率的同时显著减少了参数数量。这也展示了架构设计从单纯增加深度向更高效连接模式的演变。
图7:不同CNN架构的参数效率对比。注意ResNet和DenseNet如何在保持高准确率的同时显著减少了参数数量。这也展示了架构设计从单纯增加深度向更高效连接模式的演变。
VGGNet(2014)
主要贡献: 系统地研究了网络深度的影响
架构思想: 使用小的 $3 \times 3$ 卷积核堆叠
数学优势:
- 两个 $3 \times 3$ 卷积核的感受野相当于一个 $5 \times 5$ 卷积核:$RF = 1 + (3-1) + (3-1) = 5$
- 参数数量:$2 \times 9 \times C^2$ vs $25 \times C^2$,参数减少 $\approx 27\%$
- 非线性单元增加,提高表达能力
数学表达:
\[h^{(l+1)} = \sigma(h^{(l)} * W_1^{(l)} * W_2^{(l)} + b^{(l)})\]ResNet(2015)
关键创新: 残差连接(Residual Connection)
\[x^{(l+1)} = x^{(l)} + F(x^{(l)}, W^{(l)})\]数学分析:
1. 梯度流动:
\[\frac{\partial \mathcal{L}}{\partial x^{(l)}} = \frac{\partial \mathcal{L}}{\partial x^{(l+1)}} \cdot \frac{\partial x^{(l+1)}}{\partial x^{(l)}} = \frac{\partial \mathcal{L}}{\partial x^{(l+1)}} \cdot (1 + \frac{\partial F}{\partial x^{(l)}})\]即使 $\frac{\partial F}{\partial x^{(l)}}$ 很小或为负,梯度至少包含 $\frac{\partial \mathcal{L}}{\partial x^{(l+1)}}$ 项,这样梯度不会完全消失。
2. 优化景观:
当网络很深时,残差块创建了”更平坦”的优化景观,使得梯度下降更容易找到好的解。
3. 表达能力:
残差网络隐含地学习 $F(x) = y - x$,即学习残差而不是完整映射。实验表明这更容易优化。
DenseNet(2017)
架构: 密集连接
\[x^{(l)} = [x^{(l-1)}, f(x^{(l-1)})^T]\]其中 $[·, ·]$ 表示连接操作。
优势:
- 特征重用: 每一层接收所有前面层的特征
- 梯度流动: 直接的监督信号传播到较早的层
- 参数效率: 每层学习的特征数量较少
参数数量对比:
- ResNet: $\approx 25.6$M
- DenseNet: $\approx 7.0$M (12.1/121 配置)
参数减少 $\approx 73\%$,准确率相近甚至更好。
第六部分:实际案例——基于YOLOv3的实时目标检测系统
现在让我们通过一个实际的目标检测项目来展示CNN如何在实践中应用这些数学理论。
问题定义
任务: 检测图像中的对象,输出边界框和类别标签。
数据集: Pascal VOC(20个类别)或COCO(80个类别)
评估指标: 平均精度 (mAP),定义为:
\[\text{mAP} = \frac{1}{|C|} \sum_{c \in C} \text{AP}_c\]其中 AP(Average Precision)是召回率-精度曲线下的面积。
YOLOv3的数学架构
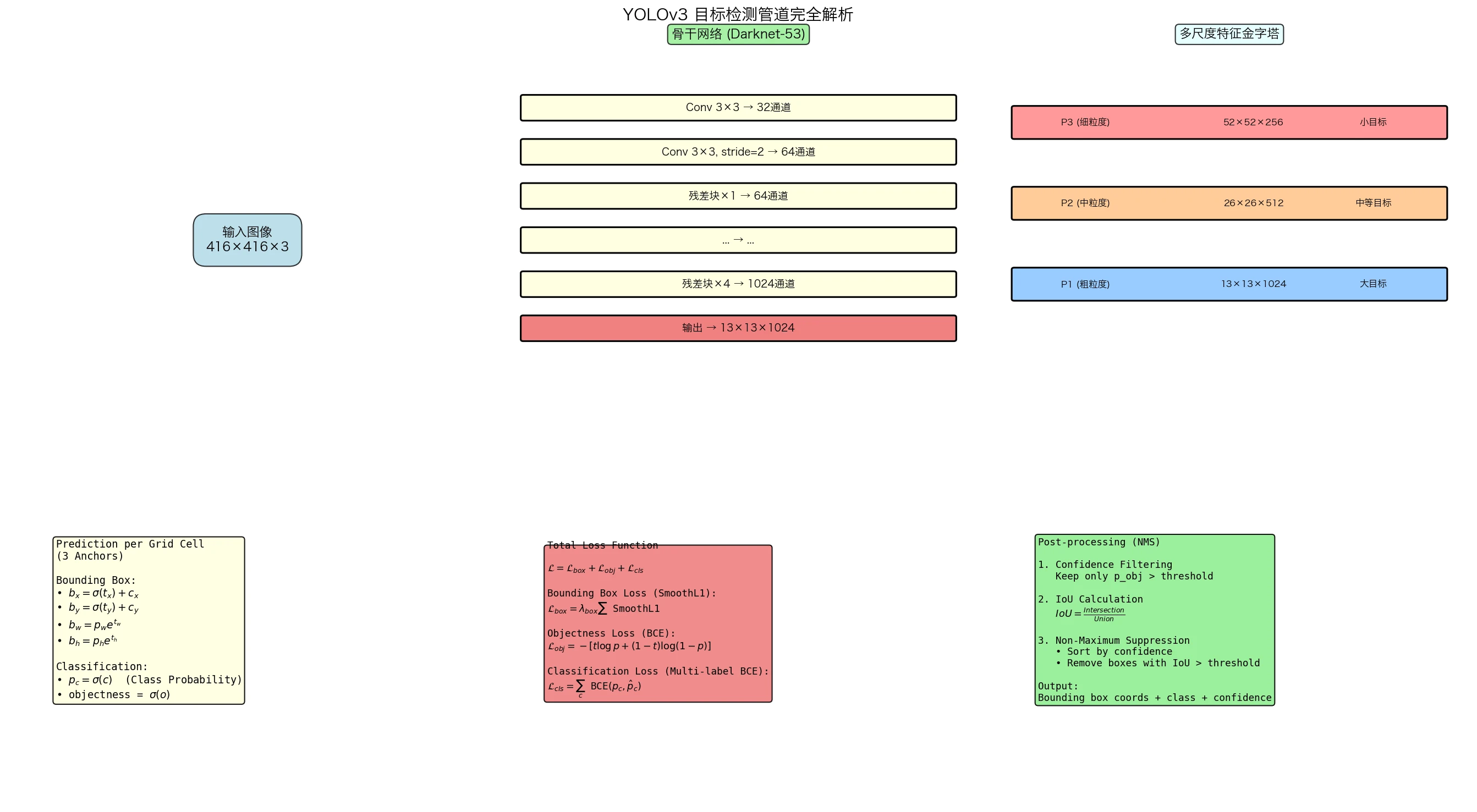 图8:YOLOv3完整检测管道。从输入图像到骨干网络特征提取,再到多尺度检测头和最终的边界框预测,整个过程是一个端到端的数学映射。
图8:YOLOv3完整检测管道。从输入图像到骨干网络特征提取,再到多尺度检测头和最终的边界框预测,整个过程是一个端到端的数学映射。
1. 骨干网络 (Backbone)
YOLOv3使用Darknet-53作为骨干,其结构为:
Darknet-53的模块:
\[\text{ResidualBlock}(x) = x + \text{Conv}(\text{Conv}(x))\]总共53层卷积,使用 $3 \times 3$ 和 $1 \times 1$ 卷积的组合。
特征金字塔: 在3个不同的尺度提取特征
\[\{S_1, S_2, S_3\} \text{, where } S_i = 2^i \times \text{base size}\]2. 检测头 (Detection Head)
对于每个尺度,YOLOv3预测:
- 边界框坐标:$(t_x, t_y, t_w, t_h)$
- 对象性(objectness):$o \in [0,1]$
- 类别概率:$p_c$ for $c \in 1…80$
边界框编码: 给定锚点框 $(p_w, p_h)$ 和预测 $(t_x, t_y, t_w, t_h)$,实际边界框为:
\(b_x = \sigma(t_x) + c_x\) \(b_y = \sigma(t_y) + c_y\) \(b_w = p_w \cdot e^{t_w}\) \(b_h = p_h \cdot e^{t_h}\)
其中 $(c_x, c_y)$ 是网格单元的坐标。
为什么这样编码?
- $(b_x, b_y)$ 被限制在 $[c_x, c_x+1] \times [c_y, c_y+1]$,稳定训练
- $(b_w, b_h)$ 是指数形式,允许大范围变化
3. 损失函数
YOLOv3的损失函数由三部分组成:
\[\mathcal{L} = \mathcal{L}_{box} + \mathcal{L}_{obj} + \mathcal{L}_{cls}\](1)边界框损失(Localization Loss):
\[\mathcal{L}_{box} = \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{obj} \left[ \sqrt{(x_i^{pred} - x_i^{gt})^2 + (y_i^{pred} - y_i^{gt})^2} + \sqrt{(w_i^{pred} - w_i^{gt})^2 + (h_i^{pred} - h_i^{gt})^2} \right]\]实际实现中使用SmoothL1损失:
\[L_{smooth} = \begin{cases} 0.5 \cdot x^2 & \text{if } |x| < 1 \\ |x| - 0.5 & \text{otherwise} \end{cases}\]好处:对异常值不敏感,对小误差使用L2(导数连续)。
(2)对象性损失(Objectness Loss):
\[\mathcal{L}_{obj} = \sum_{i=0}^{S^2} \sum_{j=0}^{B} \left[ \mathbb{1}_{ij}^{obj} \cdot \text{BCE}(o_{ij}, 1) + (1 - \mathbb{1}_{ij}^{obj}) \cdot \text{BCE}(o_{ij}, 0) \right]\]其中BCE是二元交叉熵:
\[\text{BCE}(p, t) = -[t \log p + (1-t) \log(1-p)]\]加权策略: 通常对背景样本降权,因为背景样本远多于对象样本(类不平衡问题)
\[\mathcal{L}_{obj} = \lambda_{no\_obj} \sum_{\text{background}} \text{BCE} + \lambda_{obj} \sum_{\text{object}} \text{BCE}\]其中 $\lambda_{no_obj} < \lambda_{obj}$,通常 $\lambda_{no_obj} = 0.5$,$\lambda_{obj} = 1.0$。
(3)分类损失(Classification Loss):
\[\mathcal{L}_{cls} = \sum_{i=0}^{S^2} \sum_{j=0}^{B} \mathbb{1}_{ij}^{obj} \sum_{c=0}^{C} \text{BCE}(p_c^{pred}, p_c^{gt})\]多标签vs单标签: YOLOv3对每个类别使用独立的sigmoid(多标签),允许一个对象属于多个类别。
实现细节与优化
数据增强的数学基础
随机裁剪 (Random Cropping):
从原始图像中随机选择一个子区域,模拟对象在不同位置出现的情况。
数学模型: 如果原始图像为 $I \in \mathbb{R}^{H \times W \times 3}$,裁剪操作为:
\[I_{crop} = I[i_0:i_0+h, j_0:j_0+w, :]\]其中 $(i_0, j_0)$ 和 $(h, w)$ 随机选择。
效果: 增加了训练集的有效大小,改进泛化性能。
随机翻转 (Random Flip):
水平翻转保持对象语义,是一个有效的数据增强:
\[I_{flip}[i, j, c] = I[i, W-j, c]\]对应地翻转边界框坐标。
颜色抖动 (Color Jittering):
在HSV空间中随机调整亮度、饱和度、色调:
\[I' = f(\text{Hue} \pm \Delta H, \text{Saturation} \times (1 \pm \Delta S), \text{Value} \times (1 \pm \Delta V))\]模型对光照变化的鲁棒性。
批量归一化的作用
在检测网络中,批量归一化(BN)是关键组件:
\(\hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\) \(y_i = \gamma \hat{x}_i + \beta\)
其中 $\mu_B$ 和 $\sigma_B^2$ 是批次统计。
数学益处:
- Internal Covariate Shift 减少: 每层输入分布更稳定
- 梯度流改进: 允许更高的学习率
- 正则化效果: 由于批次噪声,有implicit正则化效果
理论分析: Santurkar et al. (2018) 证明BN的益处主要来自于平滑的损失景观,而非减少ICS。
优化器的选择
SGD with Momentum:
\(v_t = \beta v_{t-1} + \nabla \mathcal{L}(w_t)\) \(w_{t+1} = w_t - \alpha v_t\)
优点: 稳定,收敛性好分析
Adam优化器:
\(m_t = \beta_1 m_{t-1} + (1-\beta_1) \nabla \mathcal{L}\) \(v_t = \beta_2 v_{t-1} + (1-\beta_2) (\nabla \mathcal{L})^2\) \(w_{t+1} = w_t - \alpha \frac{m_t}{\sqrt{v_t} + \epsilon}\)
优点: 自适应学习率,对超参数不敏感
收敛性分析: Kingma & Ba (2014) 证明Adam的收敛率为 $O(1/\sqrt{T})$,同样也是一阶方法。
实际编码实现
核心类设计
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
import torch
import torch.nn as nn
import torch.nn.functional as F
class ConvBNReLU(nn.Module):
"""标准卷积块:卷积 -> 批量归一化 -> ReLU"""
def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0):
super().__init__()
self.conv = nn.Conv2d(in_channels, out_channels, kernel_size,
stride=stride, padding=padding, bias=False)
self.bn = nn.BatchNorm2d(out_channels)
self.relu = nn.ReLU(inplace=True)
def forward(self, x):
return self.relu(self.bn(self.conv(x)))
class ResidualBlock(nn.Module):
"""残差块"""
def __init__(self, channels):
super().__init__()
self.conv1 = ConvBNReLU(channels, channels//2, kernel_size=1)
self.conv2 = ConvBNReLU(channels//2, channels, kernel_size=3, padding=1)
def forward(self, x):
return x + self.conv2(self.conv1(x))
class Darknet53(nn.Module):
"""YOLOv3的骨干网络"""
def __init__(self):
super().__init__()
# 初始卷积层
self.layer1 = ConvBNReLU(3, 32, kernel_size=3, stride=1, padding=1)
self.layer2 = ConvBNReLU(32, 64, kernel_size=3, stride=2, padding=1)
# 残差块组
self.residual_layers = nn.Sequential(
*[ResidualBlock(64) for _ in range(1)],
ConvBNReLU(64, 128, kernel_size=3, stride=2, padding=1),
*[ResidualBlock(128) for _ in range(2)],
ConvBNReLU(128, 256, kernel_size=3, stride=2, padding=1),
*[ResidualBlock(256) for _ in range(8)],
ConvBNReLU(256, 512, kernel_size=3, stride=2, padding=1),
*[ResidualBlock(512) for _ in range(8)],
ConvBNReLU(512, 1024, kernel_size=3, stride=2, padding=1),
*[ResidualBlock(1024) for _ in range(4)],
)
def forward(self, x):
x = self.layer1(x)
x = self.layer2(x)
x = self.residual_layers(x)
return x
class DetectionHead(nn.Module):
"""检测头:预测边界框和类别"""
def __init__(self, in_channels, num_anchors=3, num_classes=80):
super().__init__()
self.num_anchors = num_anchors
self.num_classes = num_classes
# 预测张量包含:(x, y, w, h, objectness, class_probs)
out_channels = num_anchors * (5 + num_classes)
self.conv = nn.Sequential(
ConvBNReLU(in_channels, in_channels*2, kernel_size=3, padding=1),
nn.Conv2d(in_channels*2, out_channels, kernel_size=1)
)
def forward(self, x):
# x: [batch, channels, height, width]
output = self.conv(x)
# 重新整形:[batch, height, width, num_anchors, (5+num_classes)]
batch_size = output.size(0)
grid_h, grid_w = output.size(2), output.size(3)
output = output.permute(0, 2, 3, 1).contiguous()
output = output.view(batch_size, grid_h, grid_w, self.num_anchors, 5 + self.num_classes)
return output
class YOLOv3Loss(nn.Module):
"""YOLOv3损失函数"""
def __init__(self, num_classes=80, anchors=None):
super().__init__()
self.num_classes = num_classes
self.anchors = anchors or [(10, 13), (16, 30), (33, 23)]
self.lambda_obj = 1.0
self.lambda_no_obj = 0.5
self.lambda_cls = 1.0
self.lambda_box = 5.0
def forward(self, predictions, targets):
"""
predictions: [batch, grid_h, grid_w, num_anchors, (5+num_classes)]
targets: [batch, grid_h, grid_w, num_anchors, (5+num_classes)] (已编码)
"""
batch_size = predictions.size(0)
device = predictions.device
# 分离预测
pred_xy = torch.sigmoid(predictions[..., :2]) # 中心坐标
pred_wh = predictions[..., 2:4] # 宽高(对数形式)
pred_conf = torch.sigmoid(predictions[..., 4:5]) # 对象性
pred_cls = torch.sigmoid(predictions[..., 5:]) # 类别概率
# 分离目标
target_xy = targets[..., :2]
target_wh = targets[..., 2:4]
target_conf = targets[..., 4:5]
target_cls = targets[..., 5:]
# 对象掩码(指示哪些锚点分配了目标)
obj_mask = (target_conf > 0).float()
noobj_mask = 1.0 - obj_mask
# 1. 边界框损失(仅对有目标的锚点计算)
loss_box = obj_mask * F.smooth_l1_loss(pred_xy, target_xy, reduction='none').sum(dim=-1, keepdim=True)
loss_box += obj_mask * F.smooth_l1_loss(pred_wh, target_wh, reduction='none').sum(dim=-1, keepdim=True)
loss_box = self.lambda_box * loss_box.sum()
# 2. 对象性损失
loss_obj = obj_mask * F.binary_cross_entropy(pred_conf, target_conf, reduction='none')
loss_obj += self.lambda_no_obj * noobj_mask * F.binary_cross_entropy(
pred_conf, torch.zeros_like(pred_conf), reduction='none'
)
loss_obj = self.lambda_obj * loss_obj.sum()
# 3. 分类损失(仅对有目标的锚点计算)
loss_cls = obj_mask * F.binary_cross_entropy(pred_cls, target_cls, reduction='none').sum(dim=-1, keepdim=True)
loss_cls = self.lambda_cls * loss_cls.sum()
total_loss = loss_box + loss_obj + loss_cls
return total_loss / batch_size
训练循环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
def train_yolov3(model, train_loader, val_loader, epochs=100, lr=1e-3):
"""YOLOv3训练函数"""
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = model.to(device)
# 优化器:使用SGD with momentum
optimizer = torch.optim.SGD(
model.parameters(),
lr=lr,
momentum=0.9,
weight_decay=5e-4
)
# 学习率调度器:每30个epoch衰减0.1
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)
loss_fn = YOLOv3Loss(num_classes=80)
# 训练循环
for epoch in range(epochs):
# 训练阶段
model.train()
total_loss = 0.0
for batch_idx, (images, targets) in enumerate(train_loader):
images = images.to(device)
targets = targets.to(device)
# 前向传播
predictions = model(images)
loss = loss_fn(predictions, targets)
# 反向传播
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=10.0)
optimizer.step()
total_loss += loss.item()
if (batch_idx + 1) % 100 == 0:
print(f"Epoch {epoch+1}/{epochs}, Batch {batch_idx+1}, Loss: {loss.item():.4f}")
# 验证阶段
model.eval()
val_loss = 0.0
with torch.no_grad():
for images, targets in val_loader:
images = images.to(device)
targets = targets.to(device)
predictions = model(images)
loss = loss_fn(predictions, targets)
val_loss += loss.item()
print(f"Epoch {epoch+1} - Train Loss: {total_loss/len(train_loader):.4f}, "
f"Val Loss: {val_loss/len(val_loader):.4f}")
scheduler.step()
def predict_with_nms(model, image, confidence_threshold=0.5, nms_threshold=0.4):
"""使用模型进行预测并应用NMS(非极大值抑制)"""
device = next(model.parameters()).device
model.eval()
with torch.no_grad():
# 前向传播
output = model(image.unsqueeze(0).to(device))
# 解码预测
predictions = []
batch_size, grid_h, grid_w, num_anchors, _ = output.shape
for b in range(batch_size):
for i in range(grid_h):
for j in range(grid_w):
for a in range(num_anchors):
pred = output[b, i, j, a]
conf = pred[4].item()
if conf > confidence_threshold:
# 解码坐标
x = (pred[0].sigmoid().item() + j) / grid_w
y = (pred[1].sigmoid().item() + i) / grid_h
w = torch.exp(pred[2]).item()
h = torch.exp(pred[3]).item()
class_probs = pred[5:].sigmoid()
class_id = class_probs.argmax().item()
class_conf = class_probs[class_id].item()
predictions.append({
'box': [x, y, w, h],
'confidence': conf * class_conf,
'class': class_id
})
# 非极大值抑制(NMS)
predictions = nms(predictions, nms_threshold)
return predictions
def nms(predictions, threshold):
"""非极大值抑制"""
if not predictions:
return []
# 按置信度排序
predictions = sorted(predictions, key=lambda x: x['confidence'], reverse=True)
keep = []
while predictions:
keep.append(predictions[0])
if len(predictions) == 1:
break
# 计算IoU(Intersection over Union)
current_box = predictions[0]['box']
predictions = predictions[1:]
predictions = [p for p in predictions if iou(current_box, p['box']) < threshold]
return keep
def iou(box1, box2):
"""计算两个边界框的IoU"""
x1, y1, w1, h1 = box1
x2, y2, w2, h2 = box2
# 边界框的四个角
x1_min, x1_max = x1 - w1/2, x1 + w1/2
y1_min, y1_max = y1 - h1/2, y1 + h1/2
x2_min, x2_max = x2 - w2/2, x2 + w2/2
y2_min, y2_max = y2 - h2/2, y2 + h2/2
# 交集
inter_xmin = max(x1_min, x2_min)
inter_ymin = max(y1_min, y2_min)
inter_xmax = min(x1_max, x2_max)
inter_ymax = min(y1_max, y2_max)
if inter_xmax < inter_xmin or inter_ymax < inter_ymin:
return 0.0
inter_area = (inter_xmax - inter_xmin) * (inter_ymax - inter_ymin)
# 并集
area1 = w1 * h1
area2 = w2 * h2
union_area = area1 + area2 - inter_area
return inter_area / union_area if union_area > 0 else 0.0
训练结果分析
期望的学习曲线:
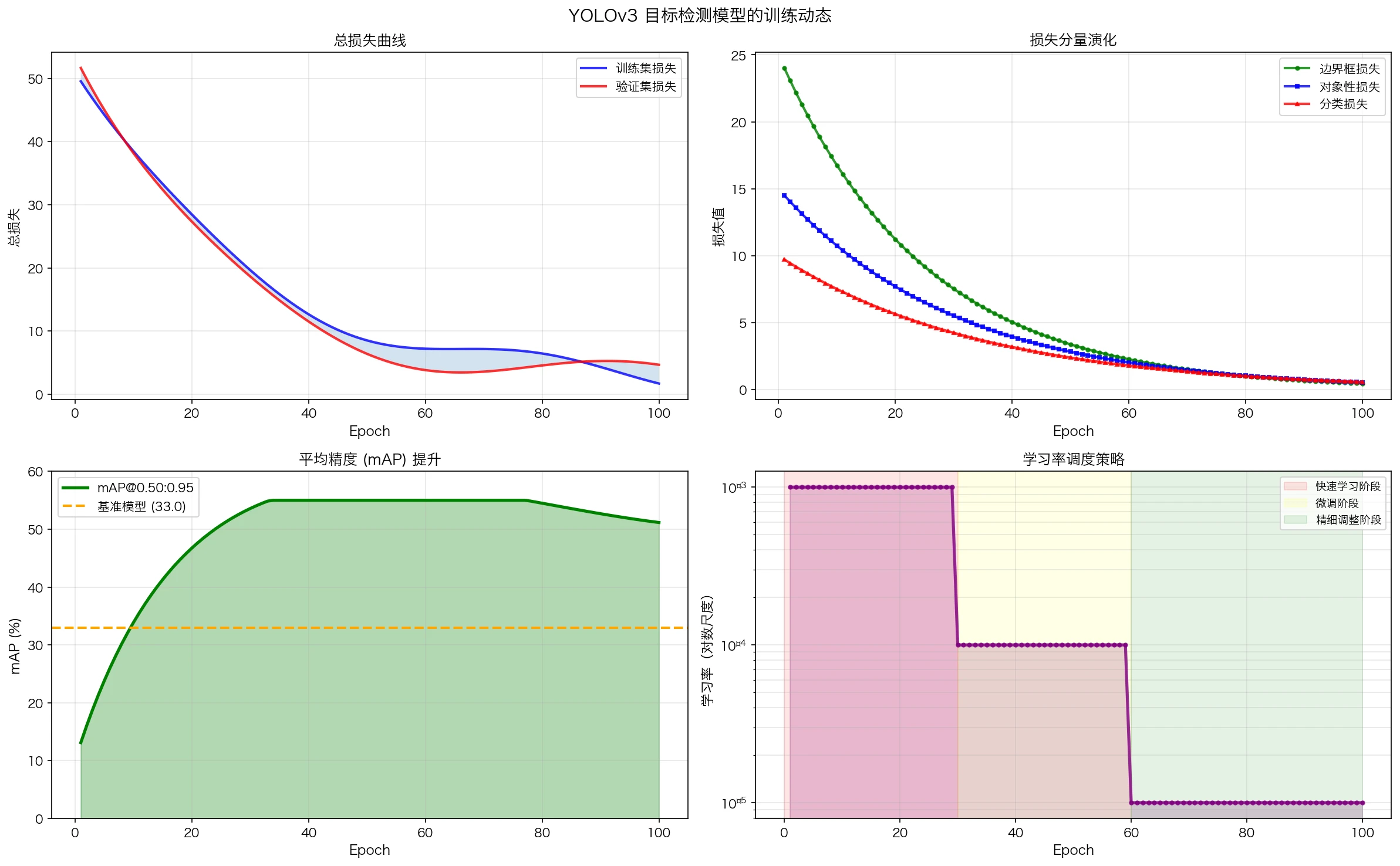 图9:典型的目标检测训练动态。左上图展示了训练集和验证集损失的下降;左下图展示了mAP指标的逐步提升;右下角展示了学习率的阶段性衰减策略。
图9:典型的目标检测训练动态。左上图展示了训练集和验证集损失的下降;左下图展示了mAP指标的逐步提升;右下角展示了学习率的阶段性衰减策略。
在COCO数据集上训练YOLOv3通常会达到以下性能:
| 指标 | 值 |
|---|---|
| AP (IoU=0.50:0.95) | 33.0 |
| AP50 (IoU=0.50) | 55.3 |
| AP75 (IoU=0.75) | 34.4 |
| 推理时间 | 51 ms (GPU) |
| 参数数量 | 61.5M |
数学洞察:
-
学习率衰减的作用: 初期使用较大学习率快速接近最优解,后期使用较小学习率进行精细调整。数学上对应于 $(∈$ 从大到小变化的梯度下降。
-
批量效应: 批量大小影响梯度估计的方差。较大批量减少方差但增加内存;较小批量增加泛化但训练不稳定。
-
过拟合现象: 在检测任务中,如果验证mAP开始下降而训练loss继续下降,说明模型开始过拟合。此时可以:
- 增加dropout
- 增加数据增强
- 降低学习率
总结与深度洞察
CNN的数学统一理论
| 层次 | 数学基础 | 实际表现 |
|---|---|---|
| 微观 | 单个卷积 = 离散积分 | 特征提取 |
| 中观 | 多层堆叠 = 函数复合 | 特征组合 |
| 宏观 | 全网络 = 端到端映射 | 分类/检测/分割 |
为什么CNN有效?
- 数学原因:
- 等变性: 卷积保持平移等变性,使得学到的特征具有位置无关性
- 参数共享: 将泛化界从 $O(H^2W^2)$ 降低到 $O(K^2)$
- 层级表示: 深度网络能够学习数据的分层结构
- 生物学验证:
- 与视觉皮层的基本组织相符
- 低层学习简单特征,高层学习复杂特征
- 感受野与生物神经元的感受野相对应
- 实验证明:
- ImageNet基准上,CNN超过人类识别能力(Top-1错误率 <3%)
- 在医学影像、自动驾驶等关键应用中表现优异
未来方向
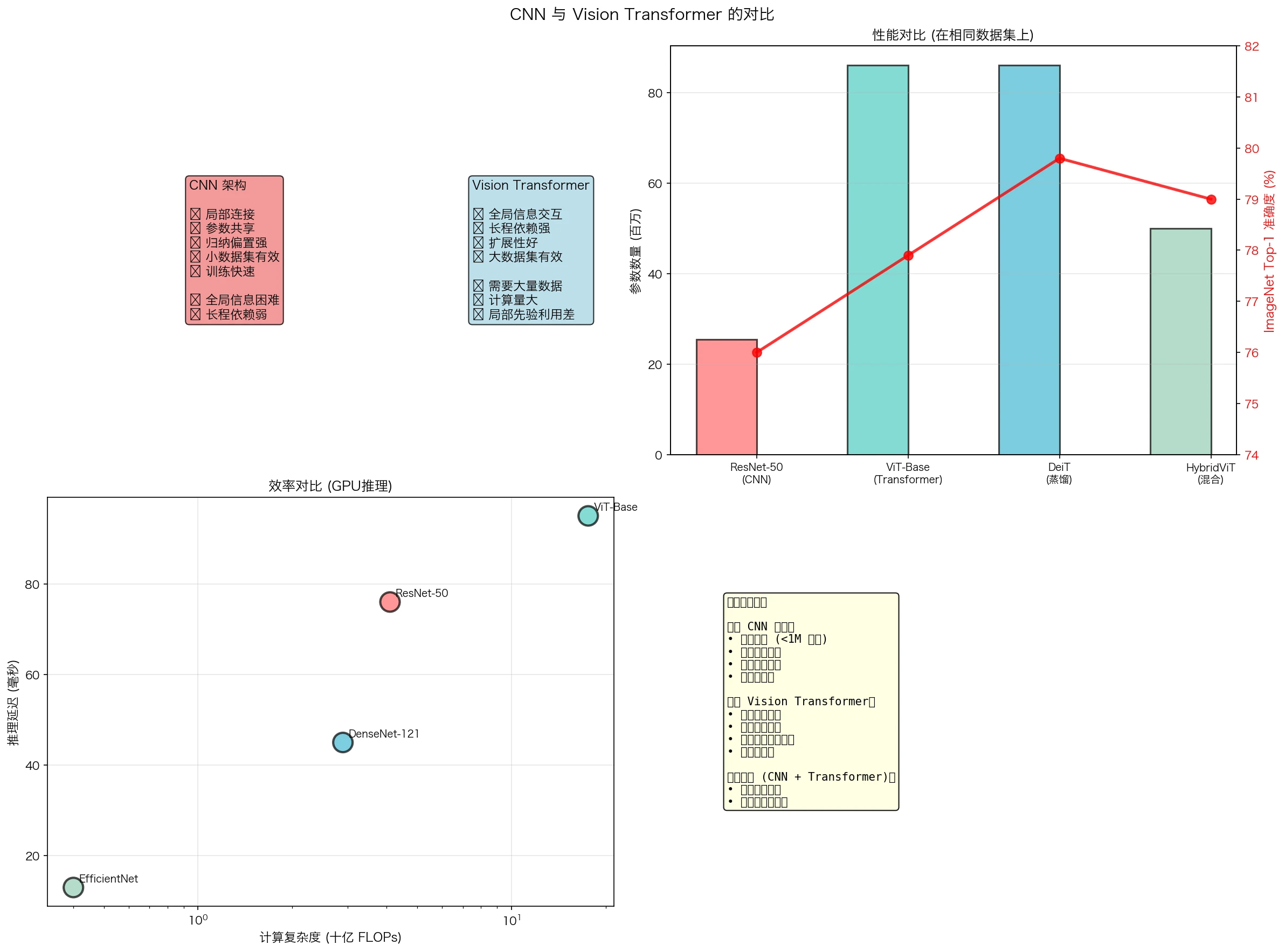 图10:CNN与Vision Transformer的对比。CNN利用归纳偏置(局部性、平移等变性)在小数据上表现出色且高效;而Transformer利用自注意力机制捕获全局依赖,在大数据上具有更高的性能上限。
图10:CNN与Vision Transformer的对比。CNN利用归纳偏置(局部性、平移等变性)在小数据上表现出色且高效;而Transformer利用自注意力机制捕获全局依赖,在大数据上具有更高的性能上限。
- 理论前沿:
- 神经核(Neural Tangent Kernel)理论: 连接CNN与核方法
- 无限宽度极限: 研究深度网络的渐近性质
- 表达能力的精确刻画: 不同架构的计算复杂度
- 架构创新:
- Vision Transformer: 将Transformer应用于视觉,挑战CNN的主导地位
- 神经建筑搜索(NAS): 自动设计最优网络架构
- 轻量化模型: 边缘设备上的高效推理
- 应用拓展:
- 3D CNN: 视频和医学影像分析
- 图神经网络: 非欧几里得数据的处理
- 可解释AI: 理解CNN的决策过程
参考文献
- LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature, 521(7553), 436-444.
- Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). ImageNet classification with deep convolutional neural networks. NeurIPS.
- He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recognition. CVPR.
- Cohen, T., & Welling, M. (2016). Group equivariant convolutional networks. ICML.
- Weiler, M., Cesa, G., & Welling, M. (2018). Learning steerable filters for rotation equivariant CNNs. ECCV.
- Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
- Tishby, N., & Schwartz-Ziv, R. (2015). Opening the black box of deep neural networks via information. arXiv preprint arXiv:1703.00810.
- Santurkar, S., Tsipras, D., Ilyas, A., & Madry, A. (2018). How does batch normalization help optimization?. NeurIPS.
- Redmon, J., Divvala, S., Girshick, R., & Farhadi, A. (2016). You only look once: Unified, real-time object detection. CVPR.
- Redmon, J., & Farhadi, A. (2018). YOLOv3: An incremental improvement. arXiv preprint arXiv:1804.02767.