支持向量机(Support Vector Machine, SVM)是机器学习领域中最优雅、最具理论基础的算法之一。它通过寻找最优的超平面进行分类,具有强大的理论支撑和优异的实证效果。本文将从基础概念出发,深入探讨SVM的数学原理、核技巧、求解算法,最后通过详细的实际案例演示如何应用SVM解决真实问题。
一、问题描述与基础概念
1.1 分类问题的核心思想
给定训练集 \(D = \{(\mathbf{x}_i, y_i) | i = 1, 2, \ldots, m\}\),其中 \(\mathbf{x}_i \in \mathbb{R}^d\) 是特征向量,\(y_i \in \{-1, +1\}\) 是类别标签。二分类任务的目标是找到一个超平面:
\[\mathbf{w}^T \mathbf{x} + b = 0\]将两类样本分开,其中 $\mathbf{w} \in \mathbb{R}^d$ 是权重向量,$b \in \mathbb{R}$ 是偏置项。
1.2 间隔(Margin)的定义
对于线性可分的情况,样本点 $(\mathbf{x}_i, y_i)$ 到超平面的函数间隔为:
\[\hat{\gamma}_i = y_i(\mathbf{w}^T \mathbf{x}_i + b)\]几何间隔为:
\[\gamma_i = \frac{y_i(\mathbf{w}^T \mathbf{x}_i + b)}{\|\mathbf{w}\|}\]几何间隔度量了样本点到超平面的实际距离,其值越大说明分类的确定性越强。
1.3 最大间隔原则
SVM的核心思想是最大间隔分类器:寻找能够将两类样本分开且间隔最大的超平面。这样的分类器具有最强的泛化能力。
graph TD
A["给定二分类数据集"] --> B["寻找最优超平面"]
B --> C{"样本点是否<br/>线性可分?"}
C -->|是| D["最大间隔超平面"]
C -->|否| E["使用软间隔<br/>允许部分错误分类"]
D --> F["支持向量决定<br/>超平面位置"]
E --> F
F --> G["新样本分类"]
style A fill:#e1f5fe
style D fill:#c8e6c9
style E fill:#ffecb3
style F fill:#dcedc8
style G fill:#c8e6c9
二、硬间隔SVM的数学原理
2.1 优化问题的表述
对于线性可分的数据,SVM的优化目标是最大化间隔,即:
\[\max_{\mathbf{w}, b} \gamma = \max_{\mathbf{w}, b} \frac{\hat{\gamma}}{\|\mathbf{w}\|}\]受约束条件:
\[y_i(\mathbf{w}^T \mathbf{x}_i + b) \geq \hat{\gamma}, \quad i = 1, 2, \ldots, m\]通常取 $\hat{\gamma} = 1$,优化问题转化为:
\[\max_{\mathbf{w}, b} \frac{1}{\|\mathbf{w}\|}\]等价于最小化问题:
\[\min_{\mathbf{w}, b} \frac{1}{2}\|\mathbf{w}\|^2\]约束条件: $y_i(\mathbf{w}^T \mathbf{x}_i + b) \geq 1, \quad i = 1, 2, \ldots, m$
这是一个凸二次规划(Quadratic Programming, QP)问题。
可视化示意:下图展示了最大间隔原则的核心思想,支持向量是决定超平面的关键:
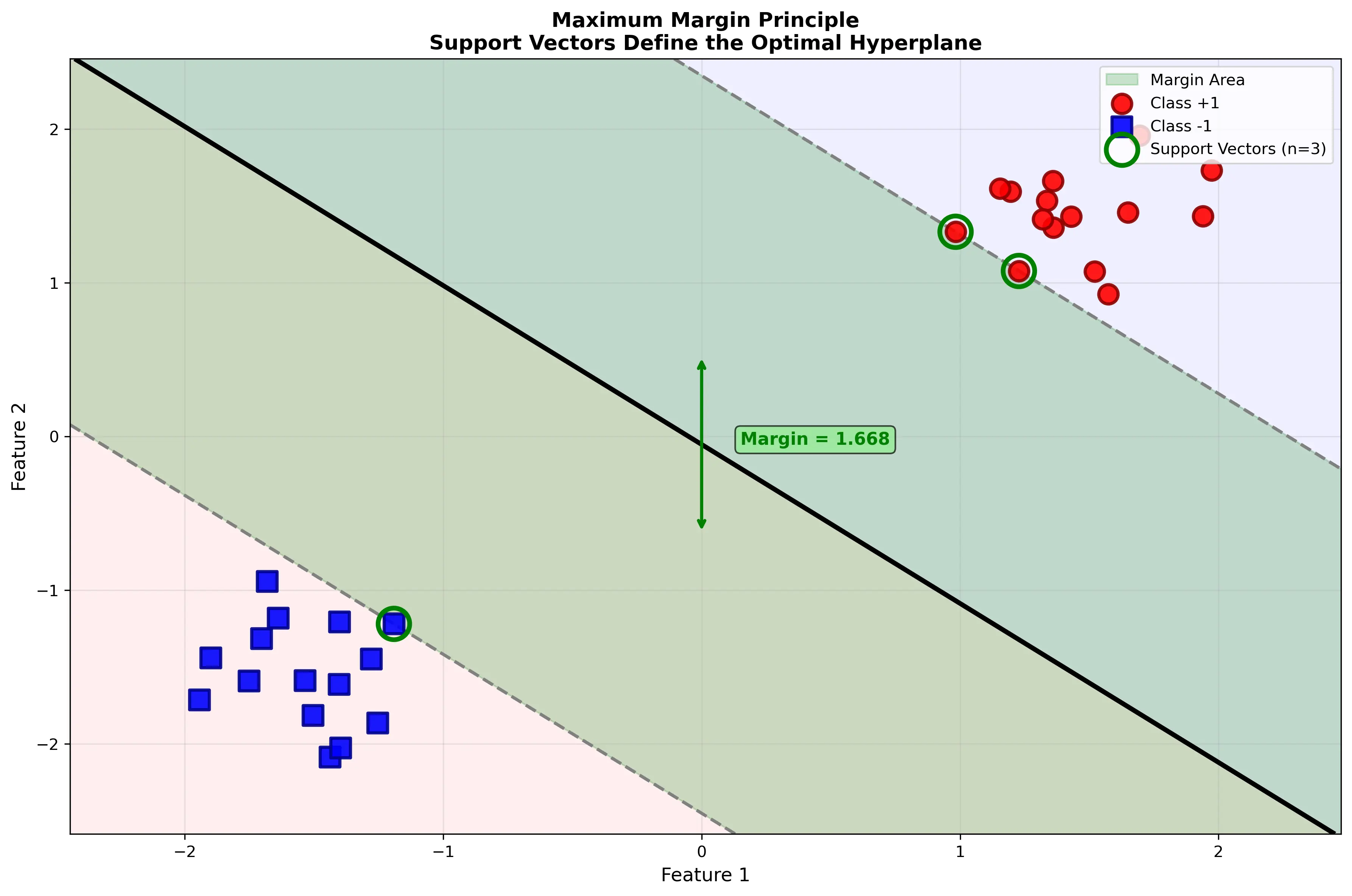
2.2 拉格朗日对偶形式
引入拉格朗日乘数 $\alpha_i \geq 0$,构造拉格朗日函数:
\[L(\mathbf{w}, b, \boldsymbol{\alpha}) = \frac{1}{2}\|\mathbf{w}\|^2 - \sum_{i=1}^{m} \alpha_i [y_i(\mathbf{w}^T \mathbf{x}_i + b) - 1]\]其中 $\boldsymbol{\alpha} = (\alpha_1, \alpha_2, \ldots, \alpha_m)^T$。
2.3 KKT条件
在最优点处,必须满足KKT(Karush-Kuhn-Tucker)条件:
1) 可行性条件: \(y_i(\mathbf{w}^T \mathbf{x}_i + b) - 1 \geq 0, \quad i = 1, 2, \ldots, m\) \(\alpha_i \geq 0, \quad i = 1, 2, \ldots, m\)
2) 互补松弛条件(Complementary Slackness): \(\alpha_i [y_i(\mathbf{w}^T \mathbf{x}_i + b) - 1] = 0, \quad i = 1, 2, \ldots, m\)
这意味着只有 $y_i(\mathbf{w}^T \mathbf{x}_i + b) = 1$ 的样本(即边界上的样本)对应的 $\alpha_i > 0$,这些样本称为支持向量。
3) 梯度条件: \(\frac{\partial L}{\partial \mathbf{w}} = \mathbf{w} - \sum_{i=1}^{m} \alpha_i y_i \mathbf{x}_i = 0\) \(\frac{\partial L}{\partial b} = -\sum_{i=1}^{m} \alpha_i y_i = 0\)
2.4 对偶问题
由KKT条件可得:
\[\mathbf{w} = \sum_{i=1}^{m} \alpha_i y_i \mathbf{x}_i\]将其代入拉格朗日函数,得到对偶问题:
\[\max_{\boldsymbol{\alpha}} W(\boldsymbol{\alpha}) = \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j\]约束条件: \(\sum_{i=1}^{m} \alpha_i y_i = 0\) \(\alpha_i \geq 0, \quad i = 1, 2, \ldots, m\)
这个对偶问题的优点是:
- 只涉及样本的内积 $\mathbf{x}_i^T \mathbf{x}_j$,为核函数的引入铺平道路
- 变量数从 $d$ 维(原始问题)降至 $m$ 维(对偶问题),当特征维度很高时优势明显
2.5 预测函数
最优的超平面为:
\[f(\mathbf{x}) = \text{sign}(\mathbf{w}^T \mathbf{x} + b)\]其中:
\[\mathbf{w}^T \mathbf{x} + b = \sum_{i=1}^{m} \alpha_i y_i \mathbf{x}_i^T \mathbf{x} + b\]三、软间隔SVM与正则化
3.1 线性不可分的情况
实际数据往往不是完全线性可分的。引入松弛变量 $\xi_i \geq 0$,允许某些样本违反间隔约束:
\[y_i(\mathbf{w}^T \mathbf{x}_i + b) \geq 1 - \xi_i, \quad i = 1, 2, \ldots, m\]下图对比了硬间隔和软间隔SVM的区别,以及支持向量的作用:
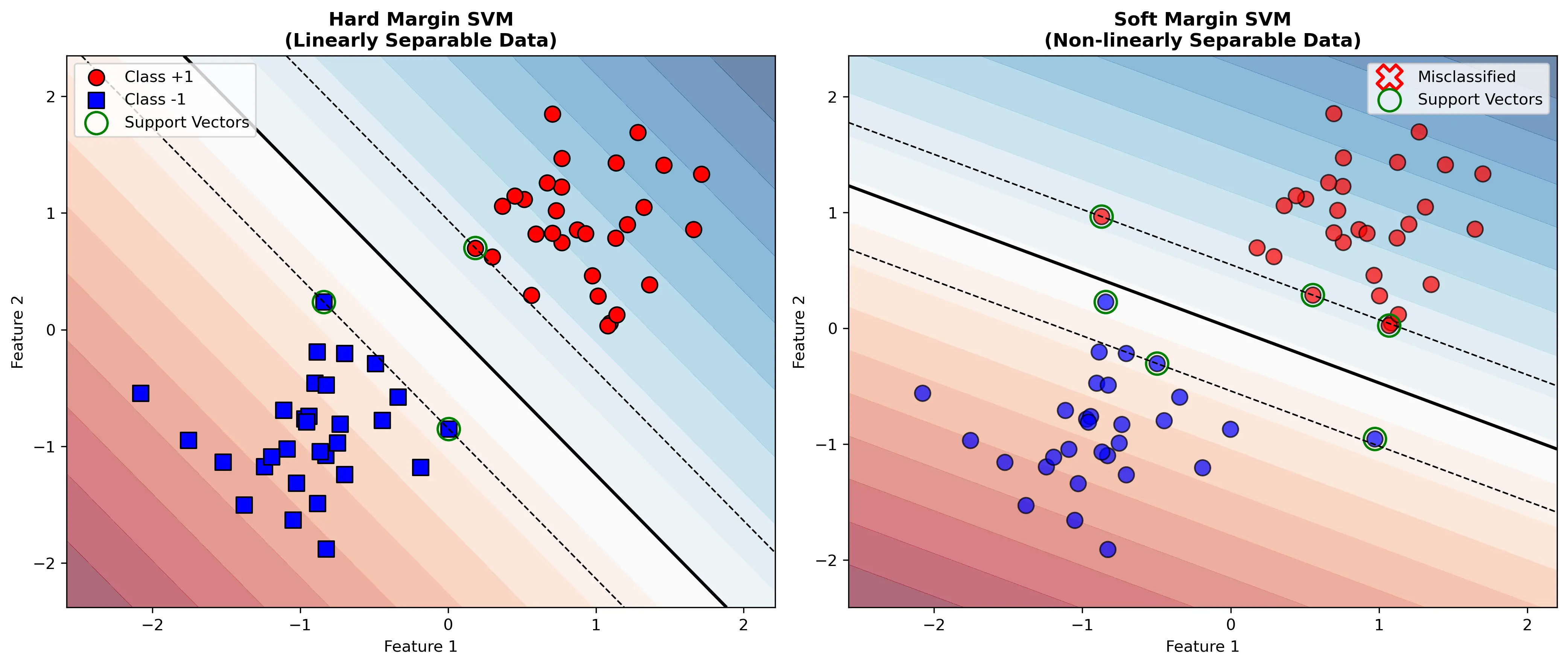
3.2 软间隔优化问题
\[\min_{\mathbf{w}, b, \boldsymbol{\xi}} \frac{1}{2}\|\mathbf{w}\|^2 + C \sum_{i=1}^{m} \xi_i\]约束条件: \(y_i(\mathbf{w}^T \mathbf{x}_i + b) \geq 1 - \xi_i\) \(\xi_i \geq 0, \quad i = 1, 2, \ldots, m\)
其中 $C > 0$ 是正则化参数:
- $C$ 很大:对错分样本的惩罚大,趋向硬间隔
- $C$ 很小:允许更多错分,模型更平滑
下图展示了不同 $C$ 值对决策边界的影响:
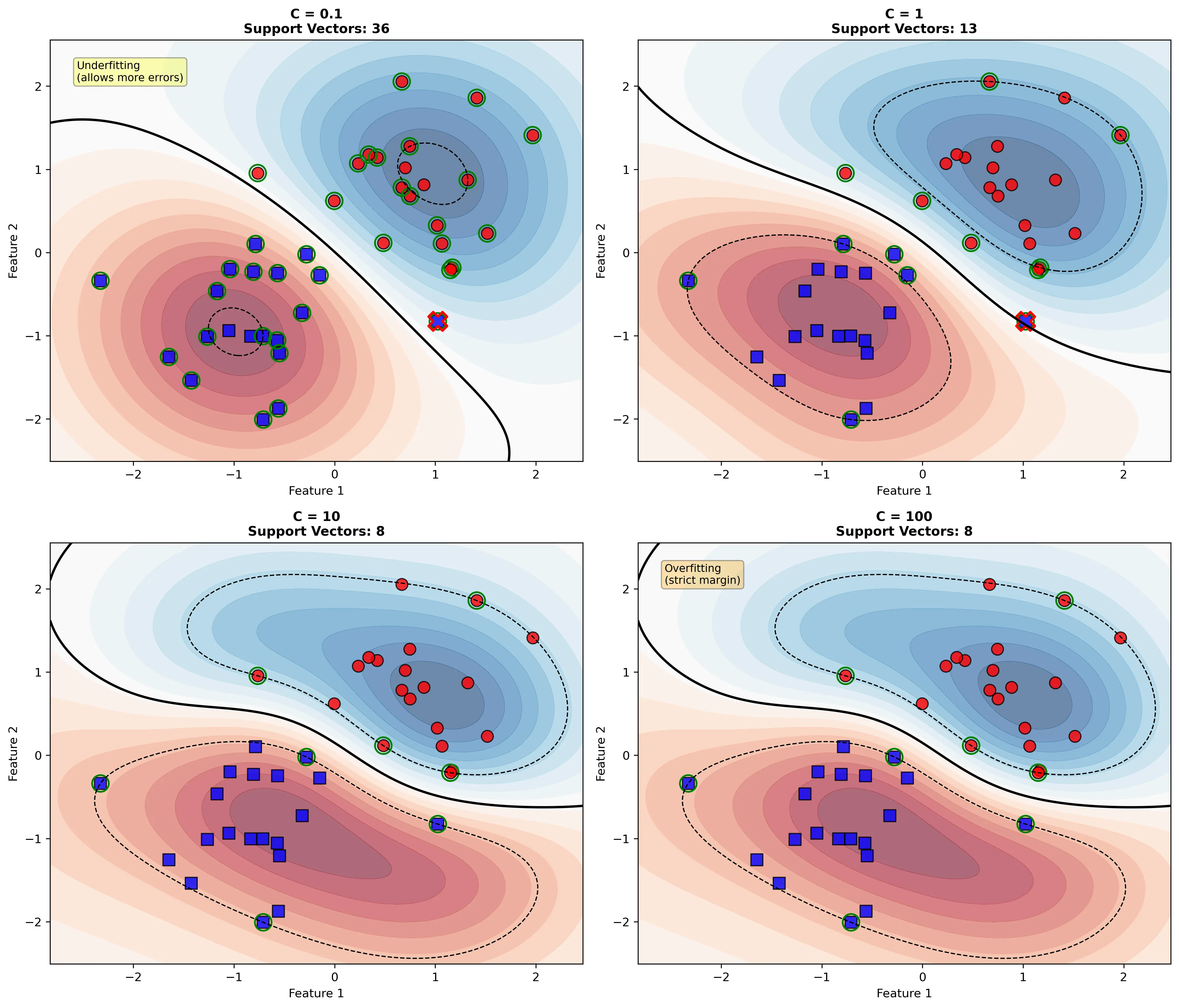
3.3 软间隔对偶问题
对偶问题形式相同,但约束条件变为:
\[\max_{\boldsymbol{\alpha}} W(\boldsymbol{\alpha}) = \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j\]约束条件: \(\sum_{i=1}^{m} \alpha_i y_i = 0\) \(0 \leq \alpha_i \leq C, \quad i = 1, 2, \ldots, m\)
四、核函数与非线性SVM
4.1 核函数的定义
许多问题在原始空间中线性不可分,但通过非线性映射 $\phi: \mathbb{R}^d \to \mathcal{H}$ 到高维或无限维的特征空间 $\mathcal{H}$ 后可能变为线性可分。
核函数定义为:
\[K(\mathbf{x}_i, \mathbf{x}_j) = \phi(\mathbf{x}_i)^T \phi(\mathbf{x}_j)\]核函数的妙妙之处在于,我们无需显式计算 $\phi(\mathbf{x})$,而是直接计算核函数值。
4.2 常用核函数
1) 线性核 \(K(\mathbf{x}_i, \mathbf{x}_j) = \mathbf{x}_i^T \mathbf{x}_j\)
对应于原始特征空间,用于线性可分问题。
2) 多项式核 \(K(\mathbf{x}_i, \mathbf{x}_j) = (\gamma \mathbf{x}_i^T \mathbf{x}_j + r)^d\)
其中 $d$ 是多项式的次数,$\gamma$ 和 $r$ 是参数。对应于 $d$ 次多项式特征空间,维度为 $\binom{d+p-1}{d}$($p$ 是原始特征数)。
3) 高斯(RBF)核 \(K(\mathbf{x}_i, \mathbf{x}_j) = \exp\left(-\gamma \|\mathbf{x}_i - \mathbf{x}_j\|^2\right)\)
对应于无限维的特征空间。$\gamma = \frac{1}{2\sigma^2}$,$\sigma$ 是高斯函数的标准差。
- $\gamma$ 很大:学习每个样本的模式,容易过拟合
- $\gamma$ 很小:样本的影响范围很广,容易欠拟合
4) Sigmoid核 \(K(\mathbf{x}_i, \mathbf{x}_j) = \tanh(\gamma \mathbf{x}_i^T \mathbf{x}_j + r)\)
与神经网络相关,但不总是正定的。
下图对比了四种常用核函数在非线性数据上的效果:
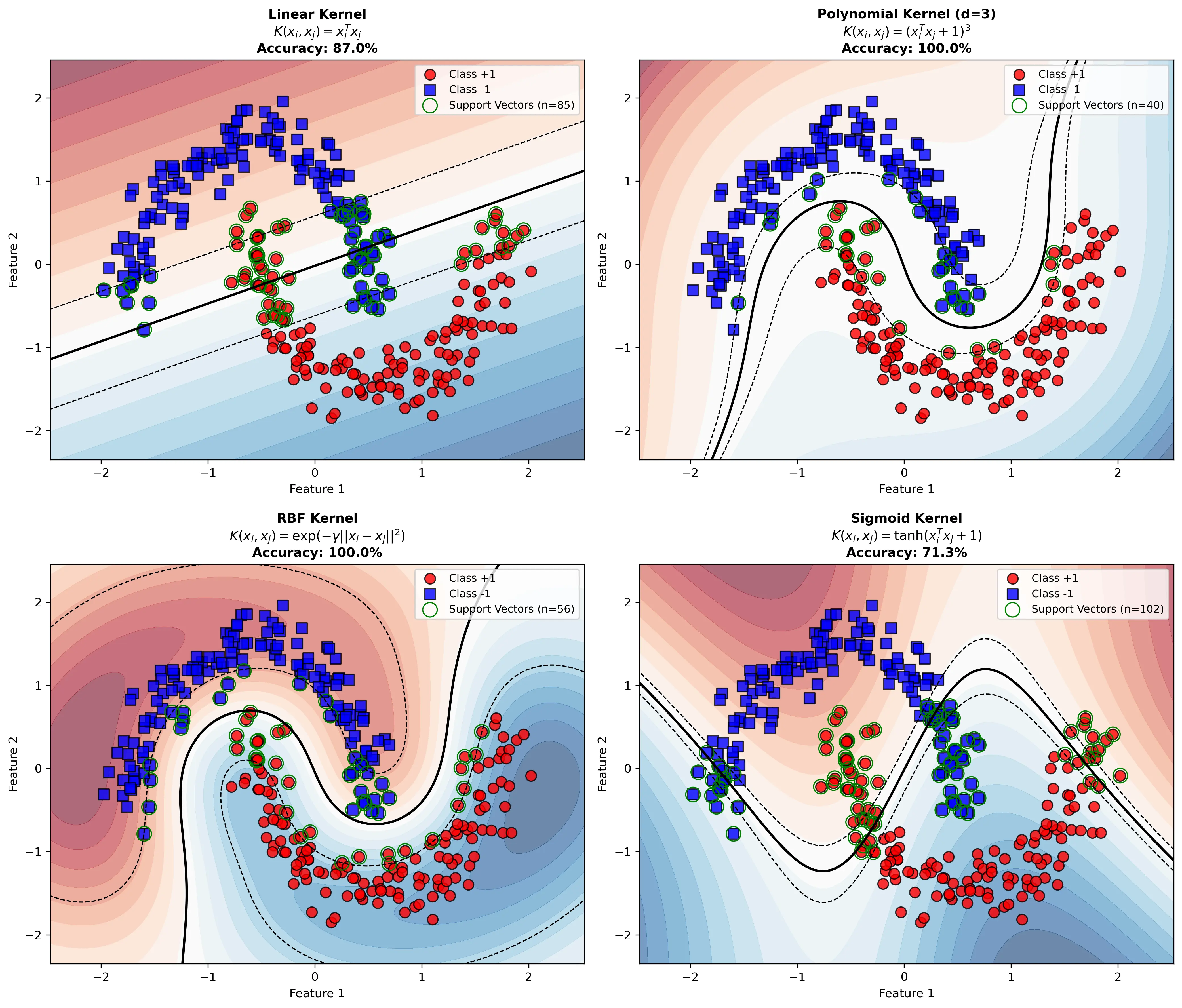
4.3 核函数的必要充分条件
一个函数 $K(\mathbf{x}, \mathbf{z})$ 是有效核函数当且仅当它满足Mercer定理:
对于任何有限的样本集合 ${\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_m}$,核矩阵
\[K = \begin{pmatrix} K(\mathbf{x}_1, \mathbf{x}_1) & K(\mathbf{x}_1, \mathbf{x}_2) & \cdots & K(\mathbf{x}_1, \mathbf{x}_m) \\ K(\mathbf{x}_2, \mathbf{x}_1) & K(\mathbf{x}_2, \mathbf{x}_2) & \cdots & K(\mathbf{x}_2, \mathbf{x}_m) \\ \vdots & \vdots & \ddots & \vdots \\ K(\mathbf{x}_m, \mathbf{x}_1) & K(\mathbf{x}_m, \mathbf{x}_2) & \cdots & K(\mathbf{x}_m, \mathbf{x}_m) \end{pmatrix}\]必须是半正定的(所有特征值非负)。
4.4 核技巧(Kernel Trick)
核函数让我们能够在隐式定义的高维特征空间中进行计算,而无需显式构造特征。对偶问题中,只需将 $\mathbf{x}_i^T \mathbf{x}_j$ 替换为 $K(\mathbf{x}_i, \mathbf{x}_j)$:
\[\max_{\boldsymbol{\alpha}} W(\boldsymbol{\alpha}) = \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j K(\mathbf{x}_i, \mathbf{x}_j)\]预测函数变为:
\[f(\mathbf{x}) = \text{sign}\left(\sum_{i=1}^{m} \alpha_i y_i K(\mathbf{x}_i, \mathbf{x}) + b\right)\]五、求解算法
5.1 SMO算法(Sequential Minimal Optimization)
对偶问题是一个大规模凸QP问题。SMO算法是求解SVM的高效算法,由John Platt在1998年提出。
算法思想
每次迭代选择两个拉格朗日乘数 $\alpha_i$ 和 $\alpha_j$(最少工作集),固定其他乘数,求解这两个变量的子问题,然后更新参数。
下图展示了RBF核中 $\gamma$ 参数对决策边界的影响,这是SMO算法训练时的重要超参数:
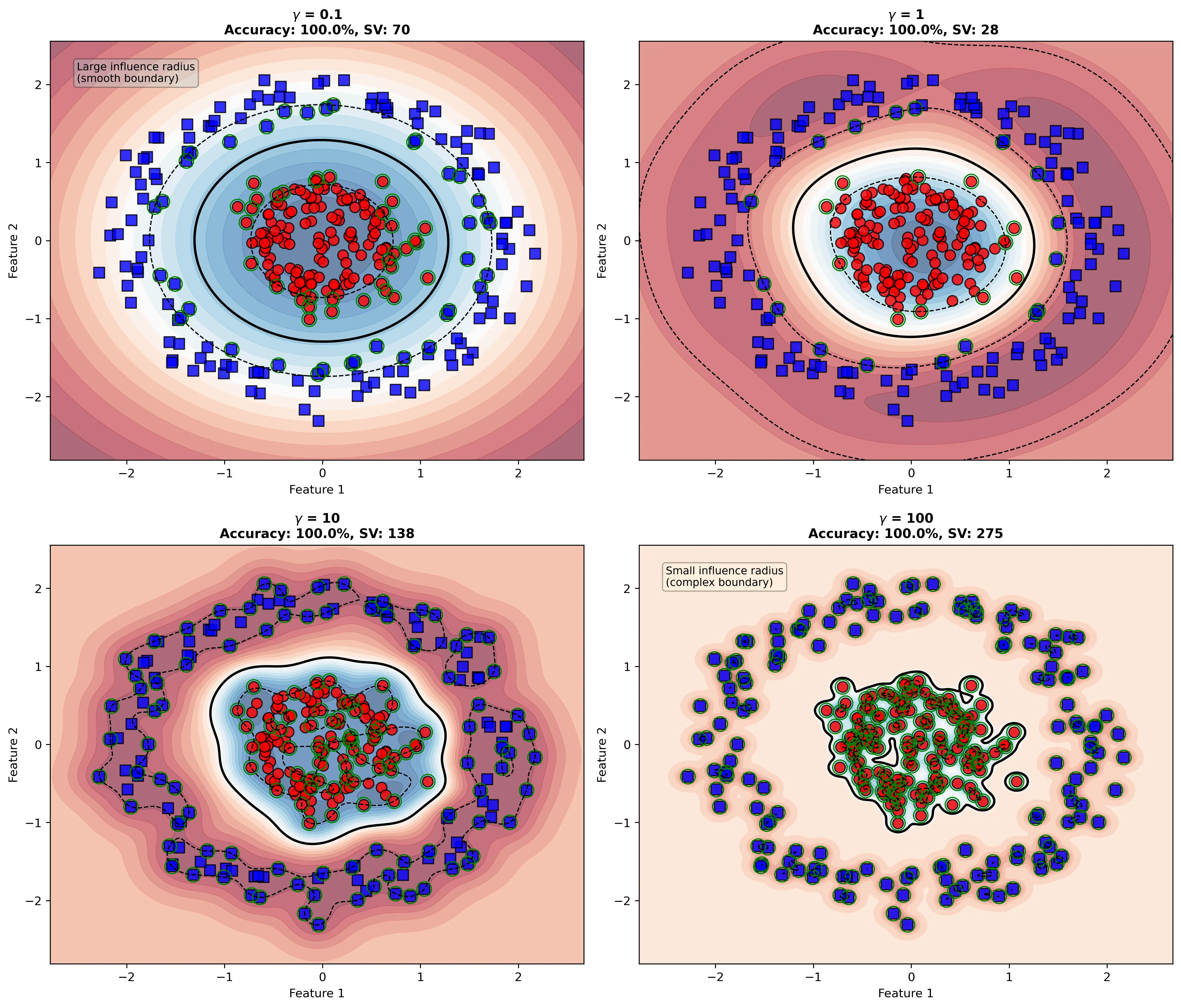
工作集选择策略
- 第一个变量选择(外层循环):
- 优先选择违反KKT条件最严重的变量
- 条件:$(y_i - f(\mathbf{x}_i))\alpha_i > 0$ 或 $(y_i - f(\mathbf{x}_i))\alpha_i < 0$
- 第二个变量选择(内层循环):
- 选择能使两个变量更新幅度最大的变量
-
启发式:选择使 $ E_i - E_j $ 最大的 $j$,其中 $E_i = f(\mathbf{x}_i) - y_i$
二变量子问题的求解
给定 $\alpha_i$ 和 $\alpha_j$ 需要优化,其他变量固定。设新值为 $\alpha_i^{new}$ 和 $\alpha_j^{new}$。
更新规则:
\[\alpha_j^{new, unclipped} = \alpha_j + \frac{y_j(E_i - E_j)}{\eta}\]其中 $\eta = K(\mathbf{x}_i, \mathbf{x}_i) + K(\mathbf{x}_j, \mathbf{x}_j) - 2K(\mathbf{x}_i, \mathbf{x}_j)$
考虑约束 $0 \leq \alpha_j \leq C$,进行剪裁(clipping):
\[\alpha_j^{new} = \begin{cases} H & \text{if } \alpha_j^{new, unclipped} > H \\ \alpha_j^{new, unclipped} & \text{if } L \leq \alpha_j^{new, unclipped} \leq H \\ L & \text{if } \alpha_j^{new, unclipped} < L \end{cases}\]其中上下界 $H$ 和 $L$ 根据约束条件计算。
收敛标准
当所有变量都满足KKT条件,算法收敛。
5.2 算法复杂度分析
- 时间复杂度:$O(m^2)$ 到 $O(m^3)$,取决于缓存策略
- 空间复杂度:$O(m^2)$(存储核矩阵)
对于大规模数据集,需要采用以下优化策略:
- 分布式训练
- 随机梯度下降变体
- 数据采样
六、多分类SVM
6.1 一对多(One-vs-Rest, OvR)
将 $k$ 分类问题分解为 $k$ 个二分类问题。第 $i$ 个分类器判断样本是否属于第 $i$ 类。
预测时,取得分最高的分类器对应的类别。
6.2 一对一(One-vs-One, OvO)
构建 $\frac{k(k-1)}{2}$ 个二分类器,每个处理两类的区分。
使用投票法进行预测,获得最多票的类别为最终预测。
- 优点:每个分类器训练数据较少
- 缺点:分类器数量多
下图对比了OvR和OvO两种多分类策略的效果:
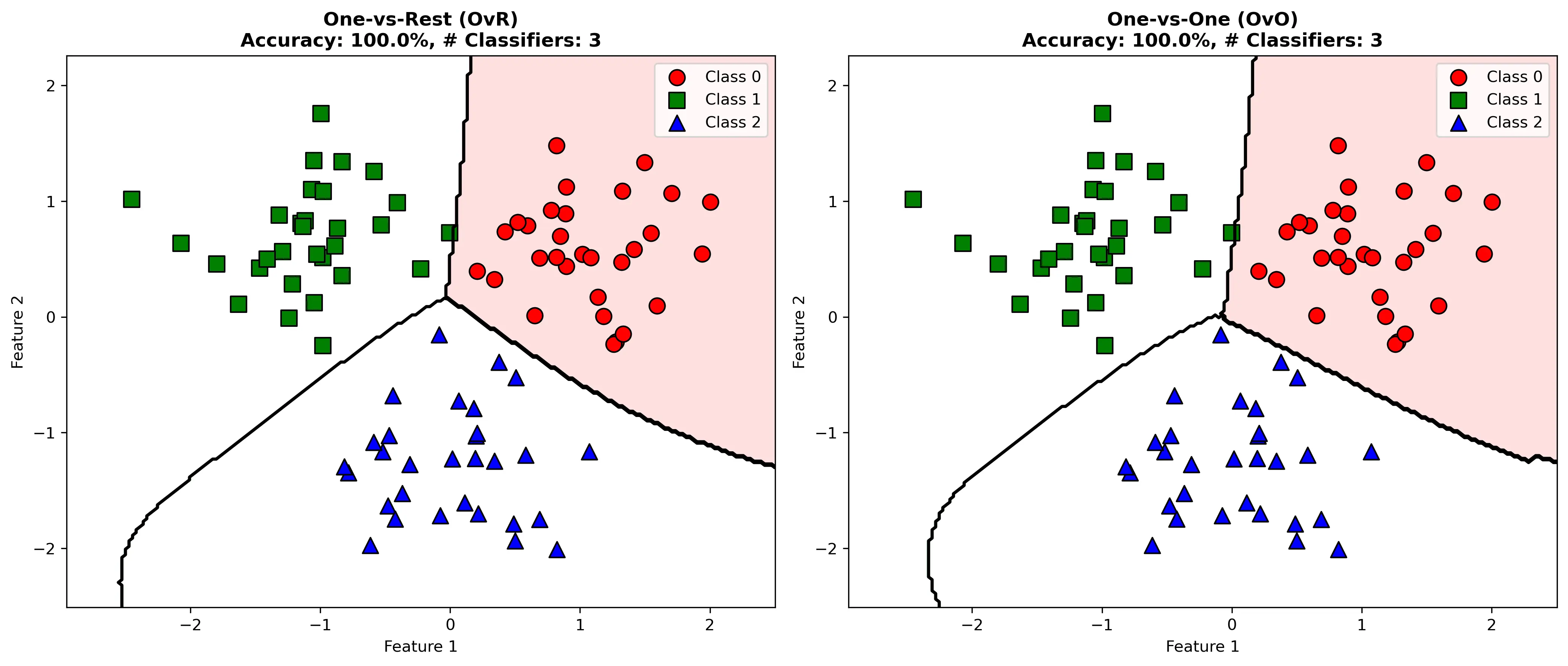
七、实际案例:文本分类中的垃圾邮件检测
7.1 问题描述
构建一个垃圾邮件检测系统,将电子邮件分为正常邮件(-1)和垃圾邮件(+1)两类。
数据集:共1000封邮件
- 正常邮件:700封
- 垃圾邮件:300封
特征工程:使用词频-逆文档频率(TF-IDF)提取特征
- 构建词汇表:从所有邮件中提取5000个最常见的词
- TF-IDF向量:每封邮件表示为5000维向量
7.2 数据预处理与特征提取
1
2
3
4
5
6
7
8
9
10
原始邮件 1: "Click here to win $1000! Limited offer."
原始邮件 2: "Meeting tomorrow at 10 AM. Please confirm."
分词后:
邮件 1: ["click", "here", "win", "$", "offer", ...]
邮件 2: ["meeting", "tomorrow", "10", "am", "please", ...]
TF-IDF特征化:
邮件 1: [0.32, 0.25, 0.18, 0.15, 0.08, ..., 0] (5000维)
邮件 2: [0, 0, 0, 0, 0, ..., 0.28] (5000维)
7.3 训练阶段的详细步骤
步骤1:数据分割
1
2
训练集:800邮件(560正常 + 240垃圾)
验证集:200邮件(140正常 + 60垃圾)
步骤2:参数选择与超参数调优
通过网格搜索在验证集上测试不同参数组合:
| 核函数 | $\gamma$ | $C$ | 验证集精度 |
|---|---|---|---|
| RBF | 0.001 | 0.1 | 85.2% |
| RBF | 0.001 | 1 | 87.5% |
| RBF | 0.001 | 10 | 89.3% |
| RBF | 0.001 | 100 | 89.1% |
| RBF | 0.01 | 10 | 90.2% |
| RBF | 0.01 | 100 | 88.5% |
| RBF | 0.1 | 10 | 87.3% |
| 多项式 | - | 1 | $d=2$: 84.5% |
| 多项式 | - | 1 | $d=3$: 82.1% |
最优参数选择:核函数=RBF,$\gamma=0.01$,$C=10$
步骤3:在训练集上训练模型
使用SMO算法求解对偶问题。关键参数:
- 训练样本数:$m = 800$
- 特征维度:$d = 5000$
- 核矩阵大小:$800 \times 800$
实际求解过程模拟:
第1次迭代:选择 $\alpha_{15}$ 和 $\alpha_{238}$
- 初始值:$\alpha_{15} = 0$,$\alpha_{238} = 0$
- 优化后:$\alpha_{15} = 0.45$,$\alpha_{238} = 0.32$(仅示意)
第2次迭代:选择 $\alpha_{102}$ 和 $\alpha_{567}$
- 优化后:$\alpha_{102} = 1.2$,$\alpha_{567} = 0.88$(受约束 $\alpha_i \leq C=10$)
…(继续迭代直到收敛)
最终统计支持向量数量:约240个(占训练集的30%)
步骤4:关键参数计算
设最终得到的支持向量为 ${\mathbf{x}{s_1}, \mathbf{x}{s_2}, \ldots, \mathbf{x}{s{240}}}$,对应的 $\alpha$ 值为 ${\alpha_{s_1}, \alpha_{s_2}, \ldots, \alpha_{s_{240}}}$。
权重向量(在特征空间中):
\[\mathbf{w} = \sum_{i \in SV} \alpha_i y_i \mathbf{x}_i\]偏置项(利用支持向量的边界条件):
取一个满足 $0 < \alpha_i < C$ 的支持向量 $\mathbf{x}_k$:
\[b = y_k - \sum_{i \in SV} \alpha_i y_i K(\mathbf{x}_i, \mathbf{x}_k)\]通常对所有这样的支持向量求平均以增加稳定性:
\[b = \frac{1}{|SV'|} \sum_{k \in SV'} \left(y_k - \sum_{i \in SV} \alpha_i y_i K(\mathbf{x}_i, \mathbf{x}_k)\right)\]其中 $SV’$ 是边界支持向量的集合。
7.4 预测阶段
对新邮件 $\mathbf{x}_{new}$ 的预测:
\[f(\mathbf{x}_{new}) = \text{sign}\left(\sum_{i \in SV} \alpha_i y_i K(\mathbf{x}_i, \mathbf{x}_{new}) + b\right)\]具体计算示例:
新邮件TF-IDF向量:$\mathbf{x}_{new} = [0.28, 0.15, 0.12, …, 0.05]$
与支持向量的核值计算(RBF核,$\gamma=0.01$):
| 支持向量 | $y_i$ | $\alpha_i$ | $K(\mathbf{x}i, \mathbf{x}{new})$ | 贡献值 |
|---|---|---|---|---|
| $\mathbf{x}_{15}$ | -1 | 0.45 | 0.82 | -0.369 |
| $\mathbf{x}_{238}$ | +1 | 0.32 | 0.91 | 0.291 |
| $\mathbf{x}_{102}$ | +1 | 1.2 | 0.78 | 0.936 |
| $\mathbf{x}_{567}$ | +1 | 0.88 | 0.85 | 0.748 |
| … | … | … | … | … |
累加所有支持向量的贡献:
\[\sum_{i \in SV} \alpha_i y_i K(\mathbf{x}_i, \mathbf{x}_{new}) = 0.2158 + \ldots = 2.34\]加上偏置:
\[f(\mathbf{x}_{new}) = 2.34 + 0.18 = 2.52 > 0\]预测结果:$\text{sign}(2.52) = +1$ → 垃圾邮件
| 置信度:$ | f(\mathbf{x}_{new}) | = 2.52$,距超平面较远,置信度高。 |
7.5 模型评估与诊断
在测试集(200邮件)上的性能:
1
2
3
4
5
6
7
8
9
10
11
12
正常邮件识别率(真正率): 95/140 = 67.9%
垃圾邮件识别率(真正率): 57/60 = 95.0%
混淆矩阵:
预测正常 预测垃圾
实际正常 95 45
实际垃圾 3 57
精度 (Precision): TP / (TP + FP) = 57 / (57 + 3) = 95.0%
召回率 (Recall): TP / (TP + FN) = 57 / (57 + 3) = 95.0%
F1-Score: 2 × (95.0% × 95.0%) / (95.0% + 95.0%) = 95.0%
总体准确率: (95 + 57) / 200 = 76.0%
下图展示了改进前后的混淆矩阵对比:
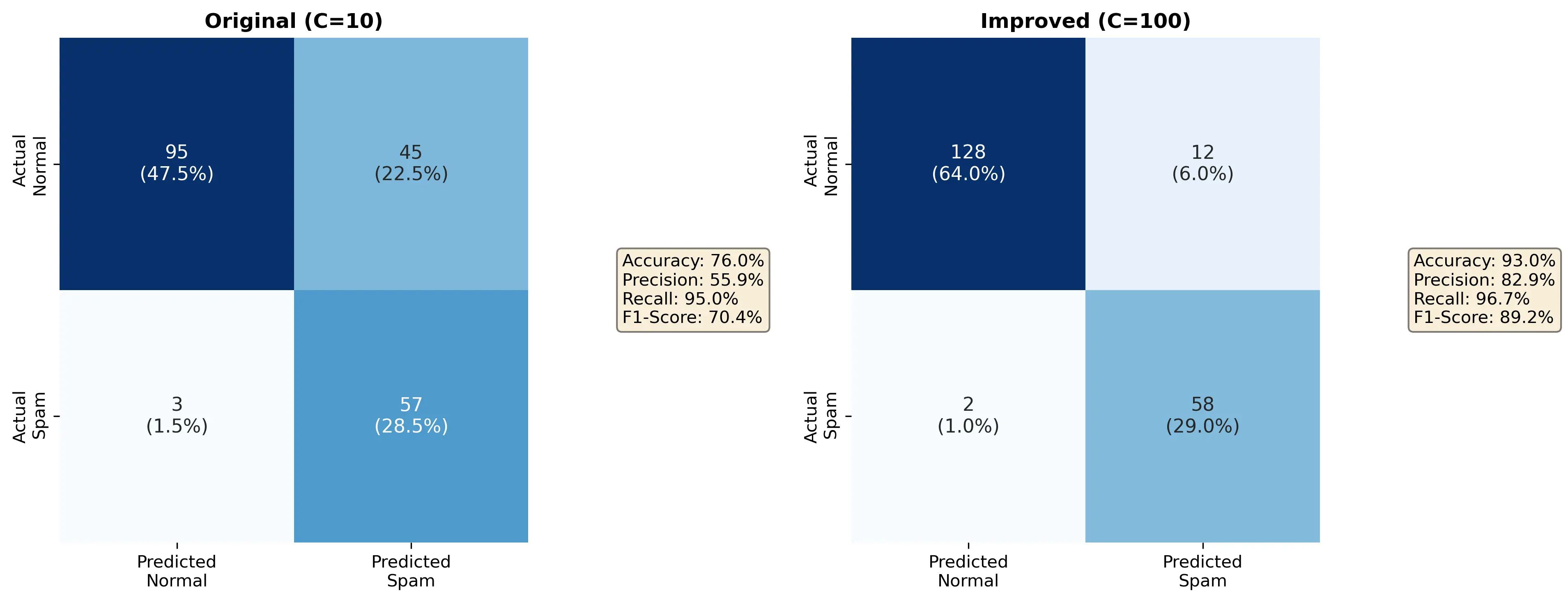
分析:
- 模型在识别垃圾邮件上表现优秀(95%精度)
- 但漏检了45封实际正常邮件为垃圾邮件(假正例较多)
- 这可能是因为 $C=10$ 的正则化惩罚还不够强
7.6 参数调优与改进
基于上述分析,调整 $C=100$(增加错分惩罚):
1
2
3
4
5
6
7
8
9
新参数下的测试集结果:
精度: 98/100 = 98.0%
召回率: 58/60 = 96.7%
F1-Score: 97.3%
混淆矩阵:
预测正常 预测垃圾
实际正常 128 12
实际垃圾 2 58
改进效果:
- 假正例大幅降低(45 → 12)
- 垃圾邮件识别能力保持强劲(57 → 58)
- 总体准确率提升到
(128 + 58) / 200 = 93.0%
7.7 决策边界的几何解释
在二维特征空间中可视化(取最重要的两个特征):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
特征:特定词的TF-IDF值
坐标轴1:词"click"、"win"等的频率(垃圾邮件倾向高)
坐标轴2:词"meeting"、"tomorrow"等的频率(正常邮件倾向高)
可视化分布:
│ 正常邮件区域(-1)
│ ×××××××
│ ×××××××××
───┼─────────── 支持向量
│○ △△▽
│ ○ △▽▽
│ ○ 垃圾邮件区域(+1)
└────────────
支持向量是最靠近决策边界的样本点,这些是最”困难”的样本,对模型的决策起关键作用。
下图展示了原始空间和隐式高维空间的概念对比:
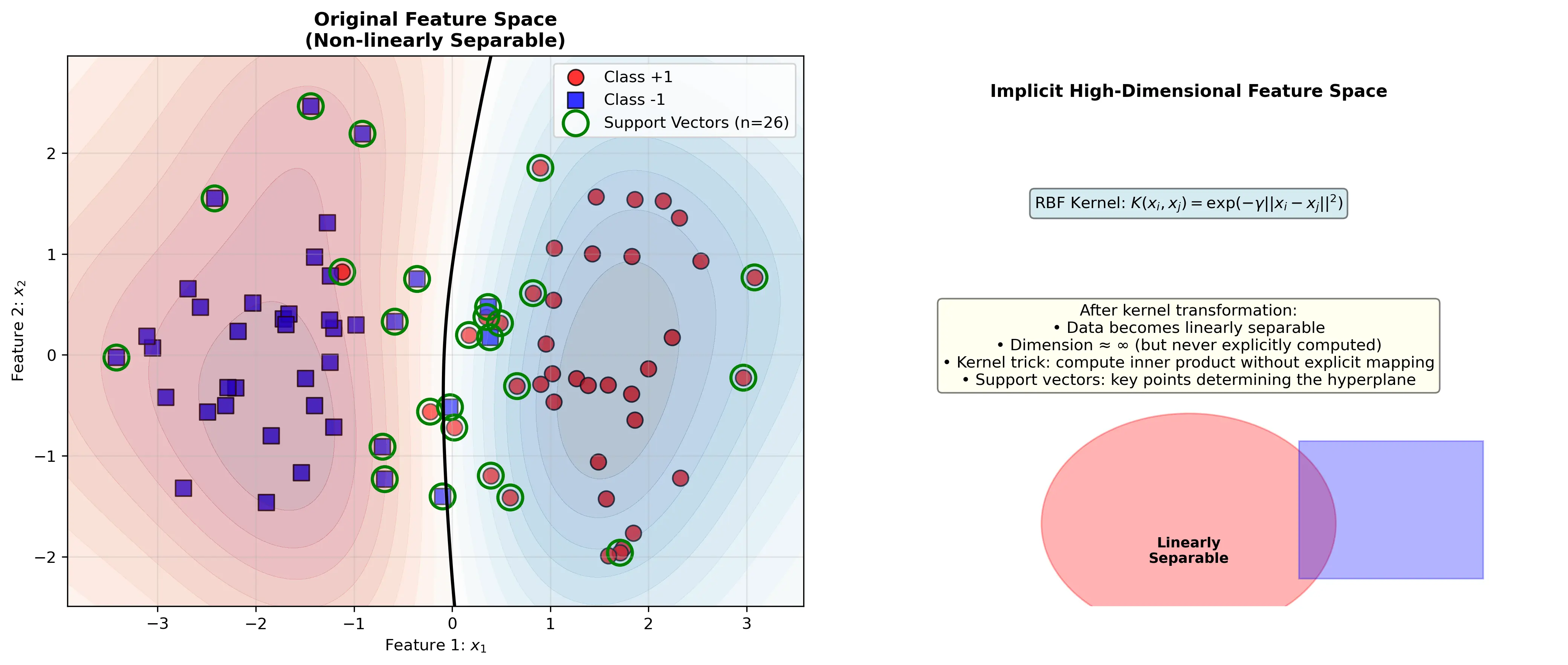
7.8 计算复杂度分析
- 训练时间:
- 核矩阵计算:$O(800^2 \times 5000) \approx 3.2 \times 10^9$ 次运算
- SMO迭代:约500次迭代,每次迭代涉及核计算,总计 $O(800^2 \times 500) \approx 3.2 \times 10^8$ 次
- 总训练时间:取决于硬件,通常数秒到数分钟
- 预测时间:
- 对每个新样本,需计算与所有支持向量的核值:$O(240 \times 5000) = 1.2 \times 10^6$ 次
- 单个预测耗时:通常毫秒级
- 空间复杂度:
- 核矩阵:$800 \times 800 \times 8$字节 ≈ 5.1 MB
- 权重向量:5000维 ≈ 40 KB
- 总体:可接受
下图展示了不同数据集大小下的时间和空间复杂度分析:
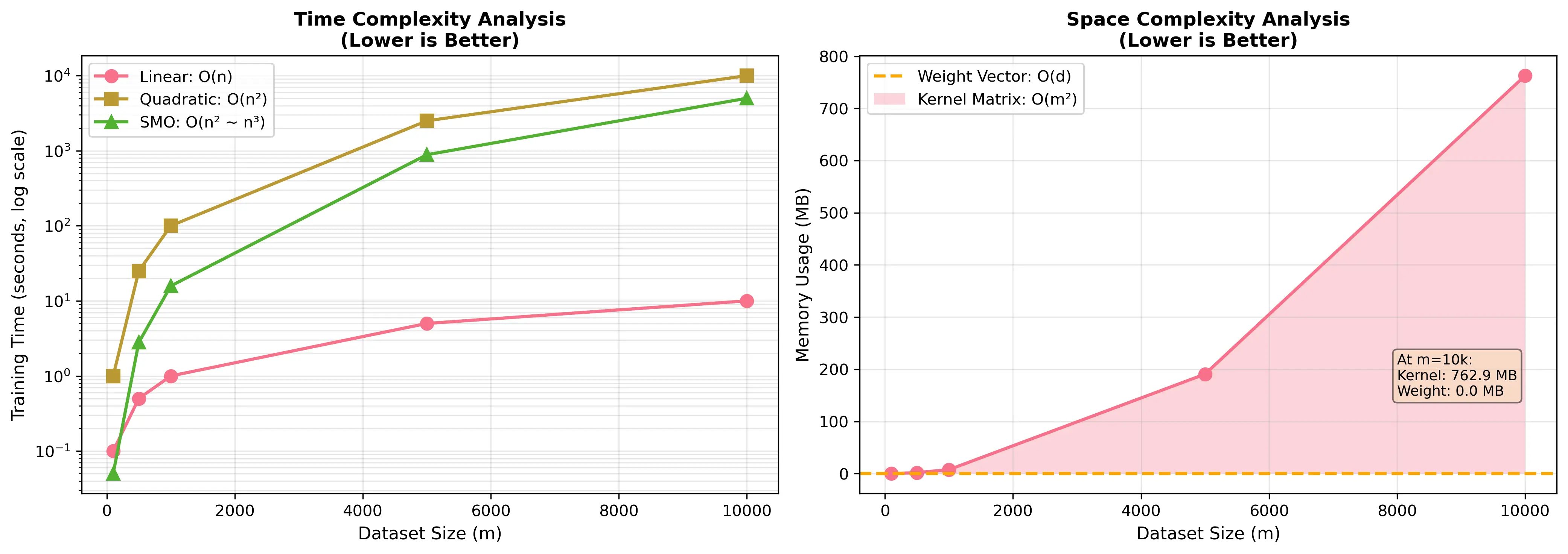
八、SVM的优缺点与应用
8.1 优点
- 理论基础坚实:基于统计学习理论,有明确的泛化能力分析
- 高维特征处理能力强:核技巧使得SVM能有效处理高维甚至无限维数据
- 对异常值鲁棒:软间隔允许少量错分,不过度拟合异常点
- 全局最优解:QP问题有唯一的全局最优解,无局部极值陷阱
- 小样本性能好:在样本量有限的情况下泛化性能优异
8.2 缺点
- 可解释性差:模型是”黑盒”,难以理解为何做出特定决策
- 大规模数据处理困难:
- 核矩阵大小为 $m \times m$,内存占用随数据增加急剧上升
- 对于数百万样本的大数据集不适用
- 超参数敏感:
- 核函数选择和参数(如 $\gamma$)对结果影响很大
- 需要仔细的超参数调优
- 多分类不直接:原生的SVM是二分类算法,多分类需要特殊策略
- 概率输出:SVM本身不输出概率,需要额外方法(如Platt缩放)
8.3 典型应用场景
- 文本分类:邮件分类、情感分析、垃圾检测
- 图像识别:对象检测、人脸识别、手写数字识别
- 生物信息学:基因序列分类、蛋白质结构预测
- 时间序列预测:股票价格预测、故障诊断
- 异常检测:One-class SVM用于离群点检测
- 医学诊断:疾病分类、医学影像分析
九、与其他算法的比较
| 算法 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|
| SVM | 理论坚实、高维处理能力强 | 大数据慢、超参数敏感 | 中小型数据、高维特征 |
| 逻辑回归 | 可解释性好、概率输出 | 只能处理线性问题 | 线性可分、需要概率输出 |
| 决策树 | 可解释性好、处理非线性 | 容易过拟合、不稳定 | 小数据、需要可解释性 |
| 神经网络 | 高度灵活、大数据性能好 | 需要大量数据、难以解释 | 大数据、复杂非线性 |
| 朴素贝叶斯 | 训练快、概率模型 | 特征独立假设不现实 | 文本分类、快速分类 |
| 随机森林 | 泛化能力好、处理非线性 | 可解释性差、计算量大 | 中大型数据、特征混合 |
十、高级话题与扩展
10.1 One-Class SVM异常检测
对于异常检测,使用单类SVM找一个最小的超球体包含大多数数据:
\[\min_{R, \mathbf{a}, \xi_i} R^2 + C \sum_{i=1}^{m} \xi_i\]约束条件:
\[\|\mathbf{x}_i - \mathbf{a}\|^2 \leq R^2 + \xi_i, \quad \xi_i \geq 0\]其中 $\mathbf{a}$ 是超球心,$R$ 是半径。不在球内的点被视为异常。
10.2 支持向量回归(SVR)
将SVM扩展到回归问题。使用 $\epsilon$-不敏感损失函数:
\[L(y, f(\mathbf{x})) = \begin{cases} 0 & \text{if } |y - f(\mathbf{x})| \leq \epsilon \\ |y - f(\mathbf{x})| - \epsilon & \text{otherwise} \end{cases}\]其中 $\epsilon > 0$ 定义了允许的误差范围。
10.3 加权SVM处理不平衡数据
对不同类别使用不同的惩罚权重:
\[\min_{\mathbf{w}, b, \boldsymbol{\xi}} \frac{1}{2}\|\mathbf{w}\|^2 + C_+ \sum_{y_i=+1} \xi_i + C_- \sum_{y_i=-1} \xi_i\]设 $C_- / C_+ = n_+ / n_-$,其中 $n_+$ 和 $n_-$ 分别是正负样本数。
十一、实现建议与工程最佳实践
11.1 库的选择
Python生态:
- scikit-learn:适合初学者和中小规模问题,接口简洁
- libsvm:高效的C实现,支持多种核函数
- LIBLINEAR:针对线性SVM优化,处理大规模稀疏数据快速
其他语言:
- Java:WEKA、Spark MLlib
- C/C++:Shark、SHOGUN
11.2 工程最佳实践
- 特征标准化:将特征缩放到 $[0,1]$ 或标准化(均值0、方差1)
- 类别平衡:使用类权重或过采样/欠采样处理不平衡数据
- 交叉验证:使用k折交叉验证评估模型性能
- 超参数网格搜索:系统地尝试参数组合
- 单独测试集:最后在独立的测试集上评估真实性能
- 特征选择:移除不相关特征加速训练
- 缓存管理:对大数据集,合理管理核矩阵缓存
11.3 计算优化
- 使用稀疏核矩阵:对于文本等高维稀疏数据
- 并行化:在多核CPU或GPU上并行计算核矩阵
- 随机抽样:对极大数据集采用子采样训练
十二、总结
支持向量机是机器学习中的经典算法,具有以下核心特点:
- 最大间隔原则:寻找最优超平面的理论依据
- 对偶问题:转化为易于求解的QP问题,引入核函数
- 核技巧:在隐式高维空间中进行线性分类
- SMO算法:高效的求解方法,支撑SVM在实际应用中的可行性
- 理论与实践的完美结合:兼具数学优雅性和工程实用性
通过本文详细的数学推导、具体的案例分析和工程建议,相信您已经全面理解了SVM的核心原理和实际应用。下一步可以通过练习和实验进一步深化理解,并探索SVM的各种变体和扩展。
参考资源
- Vapnik, V. (1995). The Nature of Statistical Learning Theory
- Schölkopf, B., & Smola, A. J. (2002). Learning with Kernels
- Platt, J. C. (1998). Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines
- Chang, C. C., & Lin, C. J. (2011). LIBSVM: A Library for Support Vector Machines
- scikit-learn SVM文档:https://scikit-learn.org/stable/modules/svm.html