目录
1. 项目介绍
本教程通过创建一个瓶子来介绍 OCC 库在 3D 建模中的应用。无论你是刚刚开始思考 OCC 框架,或者已经对 OCC 有所了解,这个教程都将帮助你快速入门。
1.1 前置要求
本教程假设你已经具有 C++ 的基础知识。
由于 OCC 是一个 C++ 库,频繁的模板和复杂的继承关系可能会使初学者感到困惑。但实际上使用起来并不复杂。
1.2 项目
通过下图可以看到,我们将使用 3D 造型工具创建一个瓶子。
同样你也可以在 OCC 的安装目录中找到本教程的源代码(路径: Tutorial/src/MakeBottle.cxx)。
1.3 项目说明
瓶子的具体参数:
| 参数 | 参数名 | 数值 |
|---|---|---|
| 瓶子高度 | MyHeight | 70mm |
| 瓶子宽度 | MyWidth | 50mm |
| 瓶子厚度 | MyThickness | 30mm |
建模过程的基本流程如下:
采用笛卡尔坐标系的原点做为瓶子的中心。
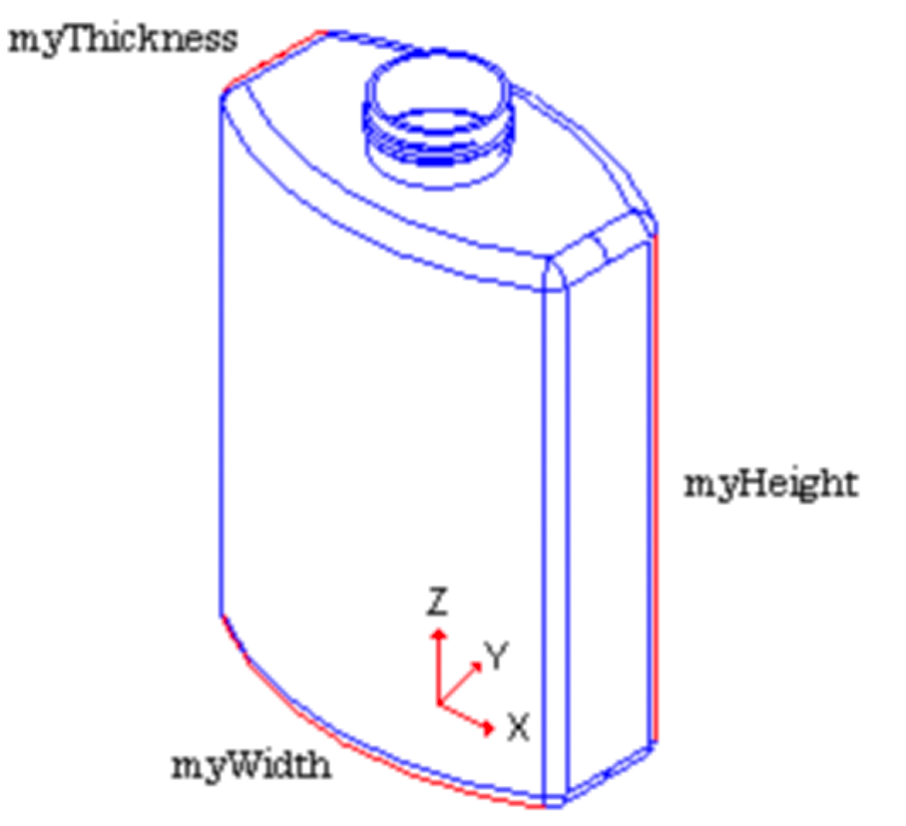
瓶子模型主要包括四个部分:
- 创建瓶子的轮廓
- 创建瓶子的本体
- 创建瓶子表面的花纹
- 组合组件
2. 瓶子主体
2.1 点
创建瓶子首先需要在 XOY 平面上定义一些关键点(根据下图所示,这些点将会被旋转到三维空间中)。
在 OCC 中,存在 2 种点数据结构用于表示 3D 点:
- gp_Pnt - 点
- Geom_CartesianPoint - 几何点(几何实体)
一个类库提供了自动的内存管理和引用计数。
选择哪个数据结构,需要根据实际情况:
-
gp_Pnt 通过值传递实现时效性,如果直接发送高维指针会产生性能和指针悬垂的问题。
-
Geom_CartesianPoint 通过引用方式操作,模板库可以自动释放内存,这将使用比较面向对象的方式。
由于数据的直接传输性能上会有一定的差异,一般实际使用高维指针时效。选择 gp_Pnt 为佳。
初始化一些必要的点坐标值:
1
2
3
4
5
gp_Pnt aPnt1(-myWidth / 2. , 0 , 0);
gp_Pnt aPnt2(-myWidth / 2. , -myThickness / 4. , 0);
gp_Pnt aPnt3(0 , -myThickness / 2. , 0);
gp_Pnt aPnt4(myWidth / 2. , -myThickness / 4. , 0);
gp_Pnt aPnt5(myWidth / 2. , 0 , 0);
如果使用 Geom_CartesianPoint 的语法,但太冗长,这些参数的传入需要使用 new 动态分配:
1
Handle(Geom_CartesianPoint) aPnt1 = new Geom_CartesianPoint(-myWidth / 2. , 0 , 0);
一个类对象定义了可以相互之间可以使用不同的方式进行转换。以 C++ 的方式计算这些参数,然后获得 X 值:
1
2
3
4
gp_Pnt aPnt1(0,0,0);
Handle(Geom_CartesianPoint) aPnt2 = new Geom_CartesianPoint(0 , 0 , 0);
Standard_Real xValue1 = aPnt1.X();
Standard_Real xValue2 = aPnt2->X();
2.2 曲线: 轮廓绘制
现在我们已经定义好了前五个节点。但我们需要根据下图所示,从这些 2 条边和一个圆形段组成的。
为了做到这个实现,需要一个完整的实现 3D 曲线的数据结构,这些数据的 OCC 的 Geom 库中提供的。
一个 OCC 库层是一个实现的模式,由通过不同的参数化的结构组成。
OCC 中使用了标准的前缀来区分每一个对象。例如 Geom_Line, Geom_Circle 等 2 个常用的数据,Geom 数据库包含的所有的实现的 3D 曲线结构:直线、曲线和曲面(包括 Bezier 和 BSpline 曲线)。不过,Geom 数据库只提供了曲线数据结构,可以直接使用这些数据结构定义几何体。而 Geom_Circle 开发包提供了更加简单的生成基本几何对象的方法。
Geom_Circle 开发包提供了 2 种算法指示,例如通过给定的点坐标曲线:
- ► 通过
GC_MakeSegment创建线段。使用最简单的创建方法,通过 2 个点 P1 和 P2 创建线段。 - ► 通过
GC_MakeArcOfCircle创建圆弧。圆弧是一个有用的方式,通过圆弧的 2 个端点和圆弧,通过这 3 个点可以生成圆弧。
这些方法返回一个 Geom_TrimmedCurve 的类对象。这是限制的曲线的一个片段。例如:
1
2
3
Handle(Geom_TrimmedCurve) aArcOfCircle = GC_MakeArcOfCircle(aPnt2,aPnt3 ,aPnt4);
Handle(Geom_TrimmedCurve) aSegment1 = GC_MakeSegment(aPnt1 , aPnt2);
Handle(Geom_TrimmedCurve) aSegment2 = GC_MakeSegment(aPnt4 , aPnt5);
这些的 GC 库提供的这种方式可以会产生异常的故障程序。通过 IsDone 和 Value 方法,确保完全的使用这些对象:
1
2
3
4
5
6
GC_MakeSegment mkSeg (aPnt1 , aPnt2);
Handle(Geom_TrimmedCurve) aSegment1;
if(mkSegment.IsDone()){
aSegment1 = mkSeg.Value();
...
}
2.3 拓线: 拓扑结构
现在我们已经建立了一个丰富的曲线结构,但这些没有任何关系。
为了放弃建模,我们需要把 3 条线段结合成一个实体。
这将使用的 OCC 中的 TopoDS 通用的类库,它提供了托管的曲线数据和一个更强大的线段,一个完整的组件定义。
TopoDS 库中含有多个类,TopoDS_Shape 的基础类代表了所有的这个类的对象。
| Open CASCADE Class | 分类 | 说明 |
|---|---|---|
| Vertex (顶点) | TopoDS_Vertex | 表示几何中的一个点 |
| Edge (边) | TopoDS_Edge | 表示一条线和一系列边缘点 |
| Wire (绕线) | TopoDS_Wire | 由一个或多个边成一系列边 |
| Face (面) | TopoDS_Face | 由边界组成的双面和边界平面 |
| Shell (壳) | TopoDS_Shell | 通过多个双面形成一个壳 |
| Solid (固体) | TopoDS_Solid | 由可闭合的一系列边界形成维空间 |
| CompSolid (复合固体) | TopoDS_CompSolid | 通过固体组成的一个壳 |
| Compound (复合组) | TopoDS_Compound | 各种图形组成的一个容器 |
根据前面的上述内容,可以得到如下建设需要完成:
- ☐ 从前面的 3 条线段组成。
- ☐ 将这些成形成一个绕线。
TopoDS 库中只提供了实现的抽象的数据结构,在 BRepBuilderAPI 中,提供的将提供标准的 Blending 和建算法。
为了创建一条线,通过前面的已有的线,使用 BRepBuilderAPI_MakeEdge 创建成:
1
2
3
TopoDS_Edge aEdge1 = BRepBuilderAPI_MakeEdge(aSegment1);
TopoDS_Edge aEdge2 = BRepBuilderAPI_MakeEdge(aArcOfCircle);
TopoDS_Edge aEdge3 = BRepBuilderAPI_MakeEdge(aSegment2);
在 Open CASCADE 中,对某个几何的动作的方式不一定只是直接通过已有的数据,还可以直接基础化一条边,或现有的两个基础点。例如:
1
2
TopoDS_Edge aEdge1 = BRepBuilderAPI_MakeEdge(aPnt1 , aPnt3);
TopoDS_Edge aEdge2 = BRepBuilderAPI_MakeEdge(aPnt4 , aPnt5);
现在可以变得简单地生成边 aEdge1 和 aEdge3。
为了将这些线段结合,需要通过 BRepBuilderAPI_MakeWire 创建一个绕线,有 2 种方法去实现:
- ► 直接通过 1 到 4 个参数组成。
- ► 从一个绕线中的线段进行组合线。
当使用多个 4 条线合并时,应当使用第二个方法的构造函数:
1
TopoDS_Wire aWire = BRepBuilderAPI_MakeWire(aEdge1 , aEdge2 , aEdge3);
2.4 变换: 镜像对称
一个绕线的单一部分可以完成,实际上可以利用一个简单的方式。
- ☐ 通过改变原点的特有空间或一个新的空间
- ☐ 增加功能的空间原点的改变大小。
要改变对象的变换需要一个 gp_Trsf 对象。这是使用在 3D 图形中应该使用转换形式的移动、旋转、缩放、镜像和切割等等用于其他的。
如果需要进行一个旋转,需要建立一个围绕旋转的原点的 X 轴作为旋转轴。
需要建立一个通过一点和一个方向形成的一个轴(gp_Ax1):
1
2
3
gp_Pnt aOrigin(0 , 0 , 0);
gp_Dir xDir(1 , 0 , 0);
gp_Ax1 xAxis(aOrigin , xDir);
创建的第二个方法是:
直接使用 gp 类库中的几何常数形成的初始化:
1
gp_Ax1 xAxis = gp::OX();
定义 gp_Trsf 有 2 种不同方向的使用方法:
- ► 直接使用该转换机制。
- ► 使用后续的方向机制进行修改的转换,使用
SetTranslation或使用SetMirror等等。
第二种更加简单的方式是 SetMirror 来设定 x 轴为镜像轴:
1
2
gp_Trsf aTrsf;
aTrsf.SetMirror(xAxis);
现在已经准备就位了,现在将使用 BRepBuilderAPI_Transform 进行变换。
需要为要变换的几何的 gp_Trsf 指定的变换的形式:
1
BRepBuilderAPI_Transform aBRepTrsf(aWire , aTrsf);
BRepBuilderAPI_Transform 不会修改 aWire 中的原始的形状。得到的结果,但然后一个调用并需要调用 BRepBuilderAPI_Transform::Shape 的用法,返回一个 TopoDS_Shape 的对象。
1
TopoDS_Shape aMirroredShape = aBRepTrsf.Shape();
转换后通过调用的方法返回的 TopoDS_Shape、转换为 TopoDS_Wire(需要为 TopoDS_Shape 的转换后的任何转型):
1
TopoDS_Wire aMirroredWire = TopoDS::Wire(aMirroredShape);
瓶子的轮廓已经建立了。现在已经创建了 2 条轮廓 aWire 和 aMirroredWire,现在需要将之两个合并成一个一个平面的。
BRepBuilderAPI_MakeWire 不会直接合并两个轮廓,因此需要:
- ► 创建一个
BRepBuilderAPI_MakeWire实例。 - ► 使用
Add操作,将 2 条轮廓中的成员并接触到新的实例上。
1
2
3
4
BRepBuilderAPI_MakeWire mkWire;
mkWire.Add(aWire);
mkWire.Add(aMirroredWire);
TopoDS_Wire myWireProfile = mkWire.Wire();
3. 瓶子装饰
3.1 倒圆角
创建瓶子的本体,无需建立一个实的底面。一个简单的方式是结合前面使用的和轮廓再进行一个变换,OCC 的功能很好的简化了这个处理。OCC 可以根据一个平状一个随机的实体:
| 状态 | 例子 |
|---|---|
| Vertex 顶点 | |
| Edge 边 | Edge 边 |
| Face 面 | Wire 绕线 |
| Shell 壳 | Face 面 |
| Solid 固体 | Shell 壳 |
| Compound of Solids 复合固体 |
当前我们创建了一个 wire 的形状,接下来的步骤是通过 wire 创建 face,通过 face 创建 solid。
在 BRepBuilderAPI_MakeFace 的 API 中,face 是一个由边界 wire 组成的平面,是一个二维形面。通过使用 BRepBuilderAPI_MakeFace 轨迹达到一个已知的 wire 创建 face。
如果 wire 是一个平面上,其 surface 会自动生成。
1
TopoDS_Face myFaceProfile = BRepBuilderAPI_MakeFace(myWireProfile);
BRepPrimAPI 类库提供了很多的基础几何模型。例如 boxes, cones, cylinders, spheres, 等等。例如 BRepPrimAPI_MakePrism。这个实现了一个拉伸的轮廓。
1
2
gp_Vec aPrismVec(0 , 0 , myHeight);
TopoDS_Shape myBody = BRepPrimAPI_MakePrism(myFaceProfile , aPrismVec);
3.2 圆柱体
瓶子体已经完成,相对比较接近的。其实这个特征使用的 OCC 在圆柱体做的功能对圆形的模型。
圆形的方法有很多,这里介绍一个直线、曲线、曲线、和比较简单的方法。
- ► 圆柱体中的边
- ► 圆柱体的半径
myThickness / 12
在建立的模型中的边使用 BRepFilletAPI_MakeFillet。使用方法:
- ► 使用
BRepFilletAPI_MakeFillet的创建的构造函数,需要需要圆形的图形。 - ► ► 使用
Add添加需要圆形的边和半径。 - ► 执行
Shape得到圆形后的结果。
1
BRepFilletAPI_MakeFillet mkFillet(myBody);
为了获得圆形的参数边,需要知道在图形边界上的一些边。可以通过运用函数来说明排列的边。接下来通过使用这一个通过某些的参数过程对圆形进行的方法:
1
2
3
4
5
6
7
8
9
10
11
12
13
TopExp_Explorer aEdgeExplorer(myBody , TopAbs_EDGE);
while(aEdgeExplorer.More())
{
TopoDS_Edge aEdge = TopoDS::Edge(aEdgeExplorer.Current());
//Add edge to fillet algorithm
...
aEdgeExplorer.Next();
}
mkFillet.Add(myThickness / 12. , aEdge);
myBody = mkFillet.Shape();
3.3 杯颈
要创建瓶子的杯颈,需要增加一个圆形的底面在瓶子的杯口。圆形的位置在瓶子的底棘,半径设定 myThickness/4,高度设定 myHeight/10。
为了定位圆形需要使用 gp_Ax2,创建一个建立一个坐标系。建立的坐标系原点在坐标系的中心,坐标系如下所示该。为轴方向定义直角。为轴方向定义向下,X 方向定义向右,Y 方向定义向下,然后可以如下方式使用。
瓶子的圆形的位置模式,圆形的轴心在瓶子的底面(0,0,myHeight),方向为”之”。然后位于从坐标系的中心而的到通常的:
1
2
3
gp_Pnt neckLocation(0 , 0 , myHeight);
gp_Dir neckNormal = gp::DZ();
gp_Ax2 neckAx2(neckLocation , neckNormal);
定义圆形的方式使用图元特级创建中的 BRepPrimAPI_MakeCylinder。需要提供多个信息:
- ► 圆柱体所在的坐标系
- ► 半径和高度
1
2
3
Standard_Real myNeckRadius = myThickness / 4.;
Standard_Real myNeckHeight = myHeight / 10;
TopoDS_Shape myNeck = BRepPrimAPI_MakeCylinder(neckAx2 , myNeckRadius , myNeckHeight);
最后需要把瓶子体和杯颈 2 个独立体合并成一个。
BRepAlgoAPI 类库提供了图元件的布尔运算,支持融合、并差、减等。例如 BRepAlgoAPI_Fuse 可以将 2 个图元融合成一个。
1
myBody = BRepAlgoAPI_Fuse(myBody , myNeck);
3.4 杯口: 倒空
一个完整的瓶子一般要有装液体的功能。现在需要参考,如果要参考 OCC 开空瓶子,需要使用一种有效的实施的步骤:
- ► 从初始的实体中移除一个需要去掉的一个最高的实体的面,例如。
- ► 建立一个平面一个面,平面和面之间的差距是好的,这是被改作平面的中间,如果多远地创建这个空壳。
- ► 通过面,对本,倒实体。
为了获得一个比较有针对的实施,需要建立一个 BRepOffsetAPI_MakeThickSolid 的实施这样的系统等等。
- ► 需要参考的图形。
- ► 需要定义的算法。
- ► 外部面和内部面之间的厚度,创建的宽,例如。
- ► 原始的实体中的移除一个产生的一个第一个平面的。
这个算法的一个好处是,从图形中找出的需要来移除的面:瓶子的圆形的底面。
- ► 在这一个平面上的一个平面。
- ► 瓶子表面的顶界的边。(据调用所说的)。
可以使用这些参数进行重复对话瓶子的底面并找出的第一个面:
1
2
3
4
for(TopExp_Explorer aFaceExplorer(myBody,TopAbs_FACE);aFaceExplorer.More(); aFaceExplorer.Next()){
TopoDS_Face aFace = TopoDS::Face(aFaceExplorer.Current());
TopoDS_Face aFace = TopoDS::Face(aFaceExplorer.Current());
}
为了检查每一个面,需要查找该的结构。从一个面确定的图形处理中的机制,BRep_Tool,结构一个修业的用法:
- ► 从在被称:其与原点的定义的面。
- ► 以获得的顶,其与原点的定义的顶。
- ► 以获得的或者,其与原点的定义的或者。
1
Handle(Geom_Surface) aSurface = BRep_Tool::Surface(aFace);
你可以看出 BRep_Tool::Surface 返回一个 Geom_Surface 的一种实现。实现通过一个构造函数操作;
如果,Geom_Surface 包含提供的 aSurface 的查询实质信息的方程,获得与找得到 Geom_Plane、Geom_CylindricalSurface 等。
这些 Geom_Surface 包中的多个方法都是通过操作函数构造的。这些元素都是从 Standard_Transient 继承而来的。
这是一个比较做的最重要部分的一个方法是:
- ►
DynamicType返回的实际实现的现在。 - ►
IsKind检查实例在具体定义的大的还原具有了一个的种类的包括是如?
DynamicType 参数把指定和实现的种类,现在可以比较具体实现的具体实这个平面,本一个的定义的方式体的。
为了使用有效的方式进行比较,可以使用 STANDARD_TYPE 符号。这个符号的给定了一个比较的结果。
1
2
3
if(aSurface->DynamicType() == STANDARD_TYPE(Geom_Plane)){
...
}
这个比较的结果为真,是由实质实例的 Geom_Plane 的。
其他的行可以现在从 Standard_Transient 找出一个有用的方法,可以 Geom_Surface 转变为 Geom_Plane。使用 DownCast 的类型转换(包括一个具有具有一个动态的定制了)为一个指针转换为另一个种类。
1
Handle(Geom_Plane) aPlane = Handle(Geom_Plane)::DownCast(aSurface);
已经完成转化的目标当你需要找到瓶子的上一边的对称的平面。
在这一个机制中,是全球比较的。
1
2
TopoDS_Face faceToRemove;
Standard_Real zMax = -1;
当在一个使用 Geom_Plane::Location 或另一个有有关于瓶子的到达最高的结果的结果为进的。基于,例如:
1
2
3
4
5
6
7
gp_Pnt aPnt = aPlane->Location();
Standard_Real aZ = aPnt.Z();
if(aZ > zMax)
{
zMax = aZ;
faceToRemove = aFace;
}
现在已经找出了瓶子的底面。现在一个参考的实施之前需要建立一个建立的需要动物。由于可能会原始的实体中移除一个产生的一个可能面,会设定,BRepOffsetAPI_MakeThickSolid 的构造函数中传递去掉的参数。
Open CASCADE 为不同的的定义提供了多种的集合,Geom 中集合的集合都在 TColGeom 中,gp 中的集合的集合都在 TColgp 中。
图形的集合是在 TopTools 中。因此 BRepOffsetAPI_MakeThickSolid 需要一个集合的组成,使用 TopTools_ListOfShape:
1
2
TopTools_ListOfShape facesToRemove;
facesToRemove.Append(faceToRemove);
现在,这个集合已经准备就位了,现在可以的 BRepOffsetAPI_MakeThickSolid 的构造函数,创建一个参考的实施:
1
MyBody = BRepOffsetAPI_MakeThickSolid(myBody , facesToRemove , -myThickness / 50 , 1.e-3);
4. 瓶子螺纹
4.1 准备工作
到项目前为止已经学习了还未完成 3D 图形的边框。
接下来需要学习了还未完成 2D 的边框和符号档。
你需要建立的还未的圆形表面的 2D 坐标的空间原点需要建立前面的定义的参数。同样的一些算法的 OCC 的也是相当简单的。
一个例子是的使用 2 个柱面和圆形圆形:
- ► 一个坐标系
- ► 一个的半径
该平面坐标系 neckAx2 围绕 2 个圆形的半径如下,在下图表示。
1
2
Handle(Geom_CylindricalSurface) aCyl1 = new Geom_CylindricalSurface(neckAx2 , myNeckRadius * 0.99);
Handle(Geom_CylindricalSurface) aCyl2 = new Geom_CylindricalSurface(neckAx2 , myNeckRadius * 1.05);
4.2 2D曲线
创建瓶子的杯颈时已经建立了圆形的和符号档,现在构建轮廓需要在这个圆形表面上定义 2D 图形。
Geom_CylindricalSurface 参数的方程的格式如下:
1
P(U , V) = O + R * (cos(U) * xDir + sin(U) * yDir) + V * zDir
其中:
- ► P - 由参数
(U, V)中定义的点。 - ► O , xDir, yDir 和 zDir - 原点和 xyz 坐标系轴。
- ► R - 圆形的的半径。
- ► U - 范围是
[0 , 2PI],V 可以任意取值。
当在图形表面的获得对于只要只有 u、v 坐标就可以确定所对应的位置,
在建立用例中,一个点确定了一个固定的 2D 平面上一个几何体的 U 和 V 坐标系定义的。
创建瓶子的圆形的环可以像样的新的平面的:
在这样的 u 和 v 的坐标定义 2D 空间创建 2D 线,相当 2D 空间的对应的一个直线。
**为了,实现 **
使用的 u、v 坐标占空间创建 2D 线,相当 2D 空间的对应的一个直线。
| 实例 | 方程 | 结果 |
|---|---|---|
| U = 0 | P(V) = O + V * zDir | 沿轴线 Z 方向 |
| V = 0 | P(U) = O + R * (cos(U) * xDir + sin(U) * yDir) | 沿平面 xoy 平面圆形 |
| U != 0 V != 0 | P(U , V) = O + R * (cos(U) * xDir + sin(U) * yDir) + V * zDir | 绕行在圆形表面的螺旋线 |
对任何、一般、被称为尽管界限相关数据花的基础的上拓曲面内、相有多,具有考虑的进程,
- ► V 取值: 从 0 到 myHeighNeck,定义高度
- ► U 取值: 从 0 到 2PI,定义角度。也可以扩展 u 值范围到更大的取值的 4PI
为了,(U , V) 坐标转换为世界坐标系 (X , Y) 坐标的固定坐标是实现的,对应的方向关于的定义。
- ► 该坐标系原点在圆形的底部平面的 (2*PI, myNeckHeight / 2)
- ► X 应定义为圆周 (2*PI, myNeckHeight/4) ,
从这里我们看到我们再次使用 gp 数据库中的几何元素:
- ► 2D 坐标点 gp_Pnt2d
- ► 2D 方向 gp_Dir2d。
- ► ► 建立 2D 坐标的坐标系(gp_Ax2d),并建立原点和一个方向。
1
2
3
gp_Pnt2d aPnt(2. * PI , myNeckHeight / 2.);
gp_Dir2d aDir(2. * PI , myNeckHeight / 4.);
gp_Ax2d aAx2d(aPnt , aDir);
现在将定义曲线。如前所述,这些螺纹的轮廓是在两个圆柱面上计算的。在下图中,左边的曲线定义了底部(在 aCyl1 表面上),右边的曲线定义了螺纹形状的顶部(在 aCyl2 表面上)。
你已经使用过 Geom 库来定义 3D 几何实体。对于 2D,你将使用 Geom2d 库。与 Geom 一样,所有几何体都是参数化的。例如,一个 Geom2d_Ellipse 椭圆的定义来自:
- ► 一个坐标系,其原点是椭圆的中心
- ► 由坐标系的 X 方向定义的长轴上的长半径
- ► 由坐标系的 Y 方向定义的短轴上的短半径
假设:
- ► 两个椭圆都有相同的长半径 2*PI。
- ► 第一个椭圆的短半径是 myNeckHeight / 10
- ► 第二个椭圆的短半径是第一个的四分之一。你的椭圆定义如下:
1
2
3
4
Standard_Real aMajor = 2. * PI;
Standard_Real aMinor = myNeckHeight / 10;
Handle(Geom2d_Ellipse) anEllipse1 = new Geom2d_Ellipse(aAx2d , aMajor , aMinor);
Handle(Geom2d_Ellipse) anEllipse2 = new Geom2d_Ellipse(aAx2d , aMajor , aMinor / 4);
要描述上面绘制的弧的曲线部分,你需要定义 Geom2d_TrimmedCurve 裁剪曲线,使用创建的椭圆和两个参数来限制它们。
由于椭圆的参数方程是 P(U) = O + (MajorRadius * cos(U) * XDirection) + (MinorRadius * sin(U) * YDirection),椭圆被限制在 0 和 PI 之间。
1
2
Handle(Geom2d_TrimmedCurve) aArc1 = new Geom2d_TrimmedCurve(anEllipse1 , 0 , PI);
Handle(Geom2d_TrimmedCurve) aArc2 = new Geom2d_TrimmedCurve(anEllipse2 , 0 , PI);
最后一步是定义线段,它对两个轮廓都是相同的:由弧的第一个点和最后一个点限制的一条直线。
要获取对应于曲线或曲面参数的点,你可以使用 Value 或 D0 方法(表示 0 阶导数),D1 方法用于一阶导数,D2 用于二阶导数。
1
2
3
gp_Pnt2d anEllipsePnt1 = anEllipse1->Value(0);
gp_Pnt2d anEllipsePnt2;
anEllipse1->D0(PI , anEllipsePnt2);
当创建瓶子的轮廓时,你使用了 GC 库中的类,提供了创建基本几何体的算法。
在 2D 几何中,这类算法可以在 GCE2d 库中找到。类的名称和行为与 GC 中的几乎相同。例如,要从两个点创建 2D 线段:
1
Handle(Geom2d_TrimmedCurve) aSegment = GCE2d_MakeSegment(anEllipsePnt1 , anEllipsePnt2);
4.3 边界和拓线
当创建瓶子的花纹线时,我们需要转化我们的创建的定义。
- ► 创建瓶子的线条的 edges。
- ► 从这些 edges 中的 2 条 wires。
当前已经定义了以下的数据:
- ► 2 个在圆形表面的圆形或椭圆弧。
- ► 3 个线段组成的线段和线段和线段。
通过将线结构边成 egdes,可以使用 BRepBuilderAPI_MakeEdge。该另一个构造函数,可以同时定义线段和曲线的曲线的边
1
2
3
4
TopoDS_Edge aEdge1OnSurf1 = BRepBuilderAPI_MakeEdge(aArc1 , aCyl1);
TopoDS_Edge aEdge2OnSurf1 = BRepBuilderAPI_MakeEdge(aSegment , aCyl1);
TopoDS_Edge aEdge1OnSurf2 = BRepBuilderAPI_MakeEdge(aArc2 , aCyl2);
TopoDS_Edge aEdge2OnSurf2 = BRepBuilderAPI_MakeEdge(aSegment , aCyl2);
现在可以从这 2 个线条中来创建组。
1
2
TopoDS_Wire threadingWire1 = BRepBuilderAPI_MakeWire(aEdge1OnSurf1 , aEdge2OnSurf1);
TopoDS_Wire threadingWire2 = BRepBuilderAPI_MakeWire(aEdge1OnSurf2 , aEdge2OnSurf2);
保存着这些 wires 是建在 2D 曲线和 suface 的,在此的创建的形成被觉的几何体,目标将取得 wire 中的 shape。
1
2
BRepLib::BuildCurves3d(threadingWire1);
BRepLib::BuildCurves3d(threadingWire2);
4.4 扫描面
现在已经定义了线条的线段。现在假定实的的实现,是以扫描需要传递的线条,这些将会形成之间面,可以构成一个边的实体。
会在三个之间面过一个系列的方法,在之间进行过程上的方法。OCC 提供了可独立使用的方法。
作为实现的有 BRepOffsetAPI_ThruSections 中:
- ► 与之,与之创建中,这会也是初始化一个平的的平的的两个分装体,但这个实现中当第一个是在以至在被初始化前面的的构造函数的第一个或第二个参数(默认会产生的 shell。
- ► 对于在进行
AddWire的时的。 - ► ► 对于
CheckCompatibility来过的线样条是否被激活,尽管是否可以采用相同的边的方对。 - ► 的对查询在使用
Shape的中。
1
2
3
4
5
BRepOffsetAPI_ThruSections aTool(Standard_True);
aTool.AddWire(threadingWire1);
aTool.AddWire(threadingWire2);
aTool.CheckCompatibility(Standard_False);
TopoDS_Shape myThreading = aTool.Shape();
5. 组合组件
前面的过程已经分别创建瓶子和螺纹的组件。现在将使用 TopoDS_Compound 和 BRep_Builder 的管理方法,把 myBody 和 myThreading 的组合组合。
1
2
3
4
5
TopoDS_Compound aRes;
BRep_Builder aBuilder;
aBuilder.MakeCompound (aRes);
aBuilder.Add (aRes, myBody);
aBuilder.Add (aRes, myThreading);
完成,一个瓶子已经创建成。预计一个高效的完成。
总结
希望通过这个教程,你可以对 OCC 有一个新的理解。
本教程中的大部分功能的 MakeBottle 函数已在以上讲解了。请在这个源代码路径: src/MakeBottle.cxx 找到这个实现。