Computer Graphics Texture Baking Rendering 3D Modeling Game Development Algorithm

纹理烘焙技术 —— 高模到低模的映射

三维表面展开以及UV坐标映射

Posted by zxh on September 23, 2025

纹理烘焙（Texture Baking）是计算机图形学中的一项核心技术，用于将高精度三维模型的细节信息（如光照、阴影、法线、环境遮蔽等）预先计算并存储到低精度模型的纹理贴图中。这项技术在游戏开发、实时渲染、离线渲染管线优化、多级LOD的精模显示等领域有着广泛应用。通过纹理烘焙，可以在保持低多边形模型性能优势的同时，获得高精度模型的视觉效果。

一、纹理烘焙基本概念

1.1 问题背景

在实时渲染应用中（如游戏、VR/AR），需要在有限的计算资源下实现高质量的视觉效果。这导致了一个核心矛盾：

  • 高精度模型：具有大量多边形，细节丰富，但渲染开销大，不适合实时应用
  • 低精度模型：多边形数量少，渲染效率高，但缺少细节，视觉效果差

纹理烘焙技术正是为了解决这一矛盾：将高精度模型的细节信息”烘焙”到低精度模型的纹理中，实现”以空间换时间”的优化策略。

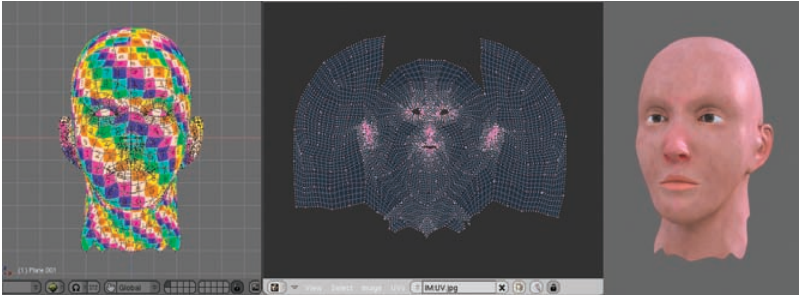
纹理映射示例

Blender下的纹理映射(LSCM)

1.2 基本思想

纹理烘焙的核心思想包括：

  1. 源模型（High-Poly Model）：高精度细节模型，包含丰富的几何细节
  2. 目标模型（Low-Poly Model）：低精度简化模型，用于实际渲染
  3. UV展开（UV Unwrapping）：将三维模型表面映射到二维纹理坐标空间
  4. 投影采样（Projection Sampling）：从高精度模型采样信息，投影到低精度模型的UV空间
  5. 纹理生成（Texture Generation）：将采样结果存储为纹理贴图
graph LR
    A["高精度模型<br/>High-Poly"] --> B["投影采样<br/>Projection"]
    C["低精度模型<br/>Low-Poly"] --> B
    D["UV展开<br/>UV Map"] --> B
    B --> E["纹理贴图<br/>Baked Texture"]
    E --> F["实时渲染<br/>Real-time Rendering"]
    
    style A fill:#e1f5fe
    style C fill:#fff3e0
    style E fill:#c8e6c9
    style F fill:#f3e5f5

1.3 烘焙类型

常见的纹理烘焙类型包括：

  1. 光照烘焙（Lightmap Baking）：将光照信息预先计算到纹理中
  2. 法线贴图烘焙（Normal Map Baking）：将高精度模型的法线信息烘焙到法线贴图
  3. 环境遮蔽烘焙（Ambient Occlusion Baking）：计算并存储环境遮蔽信息
  4. 高光贴图烘焙（Specular Map Baking）：烘焙高光反射信息
  5. 颜色/漫反射烘焙（Diffuse/Albedo Baking）：烘焙基础颜色信息
  6. ID贴图烘焙（ID Map Baking）：用于材质识别和选择

二、UV展开与纹理坐标

2.1 UV坐标系统

UV坐标是二维纹理坐标，用于将三维模型表面映射到纹理图像：

  • U轴：水平方向，范围通常为[0, 1]
  • V轴：垂直方向，范围通常为[0, 1]
  • 纹理坐标：每个顶点对应一对(u, v)坐标
1
2
3
4
5
6
7
8
9
10
11
12

// UV坐标结构
struct UVCoord {
    float u;  // 水平坐标 [0, 1]
    float v;  // 垂直坐标 [0, 1]
};

// 顶点结构（包含UV坐标）
struct Vertex {
    Vector3 position;   // 三维位置
    Vector3 normal;     // 法线
    UVCoord uv;         // UV坐标
};

2.2 UV展开算法

参数化的本质是建立一个映射函数，将三维网格上的点 $v\left(x,y,z\right)$ 映射到二维平面的 $u\left(u,v\right)$ 坐标上。

遗憾的是，根据高斯绝妙定理（Theorema Egregium），除了圆柱、圆锥这种“可展曲面”外，任何 3D 曲面在展开时都会产生扭曲。因此，UV 算法的核心目标就是：如何平衡并最小化这种扭曲。

2.2.1 三大优化目标

  1. 保角（Conformal）： 保持角度不变。贴图上的正方形在模型上还是正方形，不会变成菱形。

  2. 等面积（Equiareal）： 保持面积比例。模型上大的面，展开后依然大，保证像素密度均匀。

  3. 等距（Isometric）： 最完美的境界（角度和面积均不变），但物理上几乎不可能对复杂模型实现。

一个完整的参数化流程包含三个关键环节：

  • Segmentation（分割/切口）： 像剥橘子皮一样，必须在合适的地方“剪开”。好的算法会自动寻找高曲率或隐蔽区域作为 Seams（缝合线）。

  • Parameterization（参数化）： 运行上述 LSCM 或 ARAP 算法，将模型摊平。

  • Packing（排版）： 将展开后的各个”UV 岛”紧凑地塞进 0 到 1 的正方形方块内，榨干每一张纹理贴图的像素利用率。

2.2.2 参数化的基本数学原理

在深入探讨具体算法之前，我们需要理解参数化的数学基础。参数化的本质是建立一个映射函数，将三维网格上的点 $v(x,y,z)$ 映射到二维平面的 $u(u,v)$ 坐标上。

2.2.2.1 参数化映射

参数化映射可以形式化地表示为：

\[\phi: \mathcal{M} \subset \mathbb{R}^3 \rightarrow \Omega \subset \mathbb{R}^2\]

其中：

  • $\mathcal{M}$ 是三维网格表面（流形）
  • $\Omega$ 是二维参数域（通常是单位正方形 $[0,1]^2$）
  • $\phi$ 是映射函数，将3D点 $(x,y,z)$ 映射到2D点 $(u,v)$

映射函数通过切映射，切映射本质上是通过雅可比矩阵操作： \(J_f = \frac{\partial (x, y, z)}{\partial (u, v)} = \begin{bmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} \end{bmatrix} = [f_u, f_v]\)

设在P点的邻域内，(u,v)发生微小的变化，则其微分形式为:

\[f(u + \Delta u, v + \Delta v) = f(u, v) + J_f \begin{bmatrix} \Delta u \\ \Delta v \end{bmatrix}\]

现在对雅可比矩阵进行奇异值分解的操作: \(J_f = U \Sigma V^T = U \begin{bmatrix} \sigma_1 & 0 \\ 0 & \sigma_2 \\ 0 & 0 \end{bmatrix} V^T\)

其中雅可比矩阵解释：

  1. $V^T$ 的作用 将参数域坐标旋转到两个相互垂直的特征方向 $V_1、V_2$ 上。这两个方向对应曲面切平面椭圆的长轴和短轴方向。
  2. Σ 的作用 在新的 u、v 方向上进行伸缩变换：
    在 u 方向上伸缩 $\sigma_1$ 倍
    在 v 方向上伸缩 $\sigma_2$ 倍
    理想情况：$\sigma_1 = \sigma_2 = 1$（无缩放）
  3. U 的作用 将伸缩后的椭圆旋转到曲面的切平面上。

2.2.2.2 度量张量与第一基本形式

为了量化参数化过程中的失真，我们需要引入度量张量（Metric Tensor）的概念。

由雅可比矩阵可知： \(J_f = U \Sigma V^T\)

\[J_f^T J_f = (U \Sigma V^T)^T U \Sigma V^T = V \Sigma^2 V^T = V \begin{bmatrix} \sigma_1^2 & 0 \\ 0 & \sigma_2^2 \\ 0 & 0 \end{bmatrix} V^T = V \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \\ 0 & 0 \end{bmatrix} V^T\]

因为 $V$ 是正交矩阵，所以 $\lambda_1, \lambda_2$ 是 $J_f^T J_f$ 的特征值，并且 $\sigma_1$ 和 $\sigma_2$ 是它们的平方根，我们可以通过求 $J_f^T J_f$ 的特征值来求解 $J_f$ 的特征值。

正好，$J_f^T J_f$ 就是曲面的第一基本式*：

\[I = J_f^T J_f = \begin{bmatrix} E & G \\ G & F \end{bmatrix}\]

可得：

\[\lambda_{1,2} = \frac{1}{2} ((E + G) \pm \sqrt{4F^2 + (E - G)^2})\]

在3D曲面上，给定参数化 $\phi: (u,v) \mapsto (x,y,z)$，第一基本形式（First Fundamental Form）定义为：

\[I = \begin{pmatrix} E & F \\ F & G \end{pmatrix} = \begin{pmatrix} \phi_u \cdot \phi_u & \phi_u \cdot \phi_v \\ \phi_v \cdot \phi_u & \phi_v \cdot \phi_v \end{pmatrix}\]

其中：

  • $\phi_u = \frac{\partial \phi}{\partial u}$ 是 $u$ 方向的切向量
  • $\phi_v = \frac{\partial \phi}{\partial v}$ 是 $v$ 方向的切向量
  • $E, F, G$ 是第一基本形式的系数

理想参数化应该满足：

  • 等距映射（Isometric）：\(I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\)（单位矩阵）
  • 共形映射（Conformal）：$E = G$ 且 $F = 0$（保持角度）
  • 等面积映射（Equiareal）：$\det(I) = EG - F^2 = 1$（保持面积）

2.2.2.3 能量最小化框架

曲面的参数化方法很多， 为了衡量算法的优劣，大多数参数化算法都可以统一到能量最小化框架：

\[\min_{u} E(u) = \sum_{T \in \text{Faces}} E_T(u)\]

其中 $E_T$ 是每个三角形的局部能量：

  • Tutte：$E_T = \sum_{(i,j) \in T} |u_i - u_j|^2$（均匀权重）
  • Harmonic：$E_T = \sum_{(i,j) \in T} w_{ij} |u_i - u_j|^2$（cotan权重）
  • LSCM：$E_T = \text{Area}(T) \cdot |\nabla u - \nabla v^{\bot}|^2$（共形能量）
  • ARAP：$E_T = \sum_{(i,j) \in T} w_{ij} |(u_i - u_j) - R_i(v_i - v_j)|^2$（刚体保持）

2.2.2.4 三角形的局部线性映射

由于2.2.2.1 中3D三角形可以通过映射函数映射到参数域中，即:\(f: S \subset R^{3} \rightarrow \Omega \subset R^{2}\)。因此我们亦可以用简单的线性映射研究这个问题。 为了简化计算，我们先将每个3D三角形上创建局部坐标系，将三维三角形坐标映射为二维坐标。因此我们只需研究（X，Y）和（u，v）之间的映射关系。

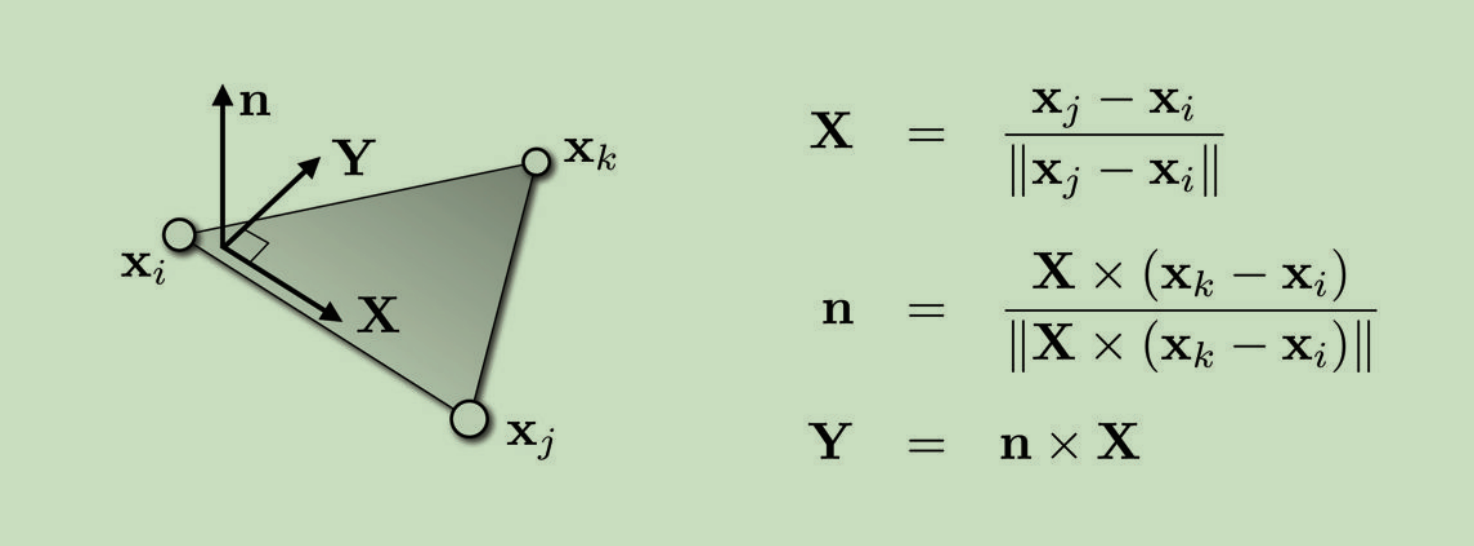
三角形中的局部X，Y坐标系

图.三角形中的局部X，Y坐标系

推导线性映射中的雅可比矩阵：

利用克拉默法则计算重心坐标

图.利用克拉默法则计算重心坐标

计算线性映射中的雅可比矩阵

图.计算线性映射中的雅可比矩阵

2.2.2.5 边界条件

参数化需要适当的边界条件来消除自由度：

  1. 固定边界（Fixed Boundary）：将边界点固定到凸多边形（如圆盘）
    • 优点：保证无翻转
    • 缺点：边界形状受限
  2. 自由边界（Free Boundary）：只固定少量点（通常2个），让边界自然优化
    • 优点：边界形状更自然
    • 缺点：可能产生翻转
  3. 混合边界（Mixed Boundary）：部分边界固定，部分自由

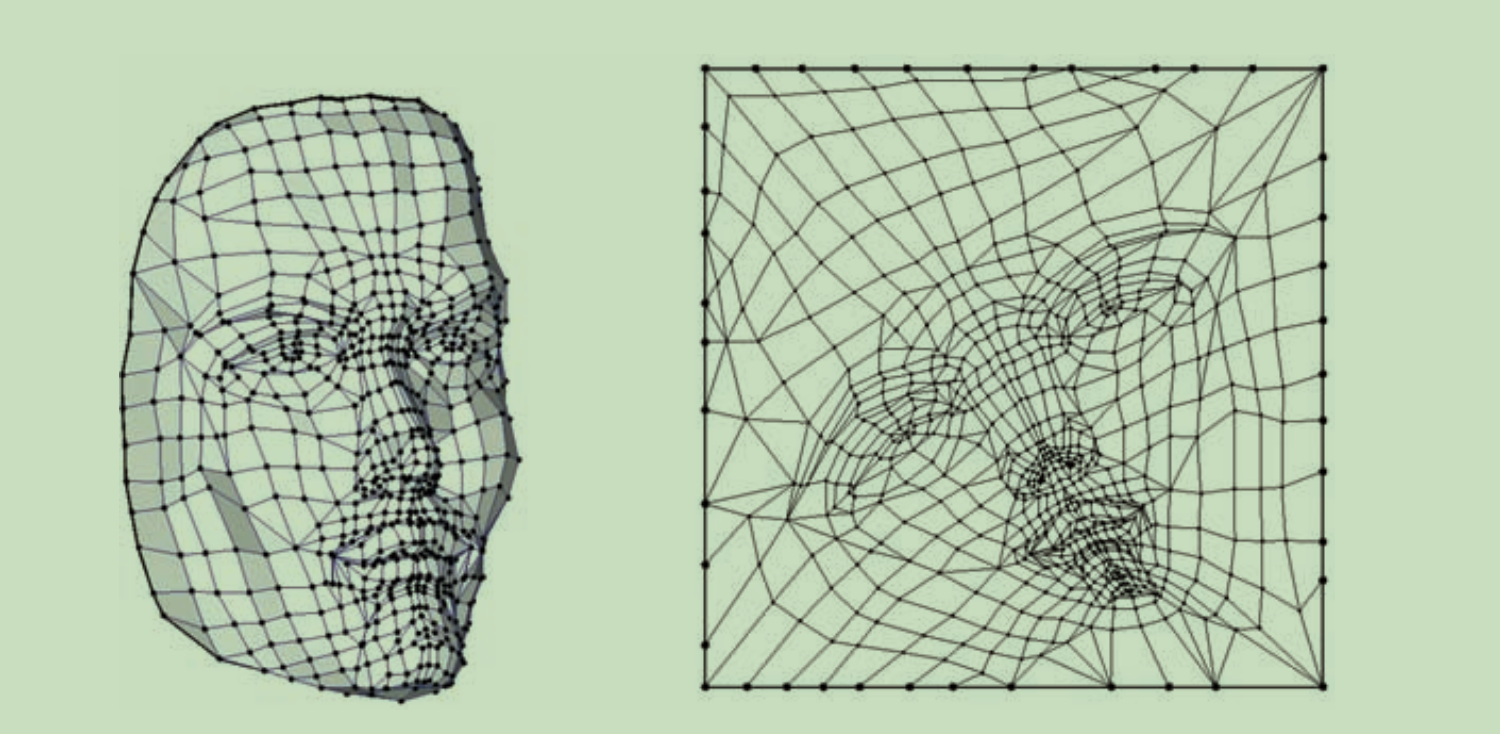
固定边界法

图.固定边界法的人脸顶点映射

2.2.3 参数化的算法

UV展开是将三维网格表面展开到二维平面的过程，主要算法包括：

2.2.3.1 基于顶点的展开（Vertex-based Unfolding）

核心思想：UV坐标直接定义到顶点上，每个顶点对应一个(u,v)，相邻三角形共用一个顶点的UV，不显式的定义seam边(接缝边)。本质上：展开的自由度定义在顶点而不是边上。

通常方法：

  • Tutte embedding
  • Harmonic parameterization
  • ARAP（As-Rigid-As-Possible）
⭐ Tutte embedding（圆盘展开参数化）

内容：把有边界的三角网格，

  • 边界点 固定在一个凸多边形(多半是圆盘)
  • 内部点 位置由“拉簧模型”自动平衡

原理：

  • 把每条边看成一个弹簧
  • 最小化总能量：
    $E = \sum_{(i,j)\in E} |u_i - u_j|^2$
    对应 图拉普拉斯方程：
    $\Delta u = 0 \quad (\text{内部点})$

优缺点：

  • 1.无反转
  • 2.对不规则物体易造成失真
  • 3.且要求边界必须是凸的
    📌 注：很多高级参数化算法的初始解就是 Tutte
⭐ Harmonic Parameterization（调和参数化）

内容：Harmonic 和 Tutte 的核心公式相同，但 Harmonic 用 cotan 权重 让参数化考虑三角形几何，Tutte 用均匀权重只做平均；Harmonic 更平滑但不保证无翻转，而 Tutte 绝对稳定但角度畸变大

对比：

方法 权重 $w_{ij}$ 数学含义 工程效果
Tutte 均匀权重 $w_{ij} = 1$ 每个邻居同等贡献 极稳定，不翻转，但几何失真大
Harmonic Cotan 权重 $w_{ij} = \frac12 (\cot \alpha_{ij} + \cot \beta_{ij})$ 考虑三角形几何形状 保留更多局部角度信息，更接近平滑/共形

优缺点：

  • 1.局部更平滑、接近共形
  • 2.不能保证不翻转（尤其边界不凸或切割不好）
    📌 注：很多高级参数化算法的初始解也可以是 Harmonic

参数化整体思路演示

图.利用弹簧系统解释参数tutte原理
⭐ ARAP（As-Rigid-As-Possible）参数化

内容：ARAP是一种局部刚体保持的参数化方法，核心思想是最小化每个局部区域的非刚体变形。与Tutte和Harmonic不同，ARAP不仅考虑顶点位置，还考虑每个三角形（或局部区域）的旋转和缩放，试图让每个局部区域尽可能保持刚体变换，从而在参数化过程中最大程度保留原始几何形状。

原理：

  • 对每个三角形（或顶点邻域），计算其从3D到2D的最优相似变换矩阵
  • 最小化能量函数：
    $E_{\text{ARAP}} = \sum_{i=1}^{n} \sum_{j \in N(i)} w_{ij} |(u_i - u_j) - R_i (v_i - v_j)|^2$

其中：

  • $u_i, u_j$ 是2D参数化坐标
  • $v_i, v_j$ 是3D原始坐标
  • $R_i$ 是顶点 $i$ 的最优旋转矩阵（2×2旋转矩阵）
  • $w_{ij}$ 是权重（通常使用cotan权重）

  • $N(i)$ 是顶点 $i$ 的邻域

  • 求解过程采用交替优化：
    1. 固定旋转：给定当前旋转矩阵 $R_i$，求解最优UV坐标（线性系统）
    2. 固定UV坐标：给定当前UV坐标，计算最优旋转矩阵（SVD分解）
    3. 迭代直到收敛

算法流程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

// ARAP参数化伪代码
void arapParameterization(const Mesh& mesh, UVMap& uvMap) {
    // 1. 初始化UV坐标（可用Tutte或Harmonic作为初始解）
    initializeUV(mesh, uvMap);
    
    // 2. 迭代优化
    for (int iter = 0; iter < maxIterations; ++iter) {
        // 2.1 固定UV，计算每个顶点的最优旋转矩阵
        std::vector<Matrix2f> rotations;
        for (int i = 0; i < mesh.vertices.size(); ++i) {
            Matrix2f R = computeOptimalRotation(mesh, uvMap, i);
            rotations.push_back(R);
        }
        
        // 2.2 固定旋转，求解最优UV坐标（线性系统）
        solveLinearSystem(mesh, rotations, uvMap);
        
        // 检查收敛
        if (energyChange < threshold) break;
    }
}

// 计算顶点i的最优旋转矩阵
Matrix2f computeOptimalRotation(
    const Mesh& mesh, 
    const UVMap& uvMap, 
    int vertexIdx
) {
    // 构建协方差矩阵
    Matrix2f S = Matrix2f::Zero();
    Vector2f center3D, center2D;
    
    for (int j : mesh.neighbors[vertexIdx]) {
        float w = cotanWeight(vertexIdx, j);
        Vector3f e3D = mesh.vertices[j] - mesh.vertices[vertexIdx];
        Vector2f e2D = uvMap.getUV(j) - uvMap.getUV(vertexIdx);
        
        // 投影到切平面（简化处理）
        Vector2f e3D_proj = projectToTangentPlane(e3D, mesh.normals[vertexIdx]);
        
        S += w * e2D * e3D_proj.transpose();
    }
    
    // SVD分解求最优旋转
    Eigen::JacobiSVD<Matrix2f> svd(S, Eigen::ComputeFullU | Eigen::ComputeFullV);
    Matrix2f R = svd.matrixV() * svd.matrixU().transpose();
    
    // 确保是旋转矩阵（det=1）
    if (R.determinant() < 0) {
        Matrix2f V = svd.matrixV();
        V.col(1) *= -1;
        R = V * svd.matrixU().transpose();
    }
    
    return R;
}

优缺点：

  • 优点：
      1. 保持局部形状：每个三角形尽可能保持原始形状和角度
      1. 低失真：相比Tutte和Harmonic，几何失真更小
      1. 适合复杂模型：对不规则形状和复杂拓扑有更好的表现
      1. 可控性强：可以通过约束边界点来控制参数化结果
  • 缺点：
      1. 计算开销大：需要迭代优化，比Tutte和Harmonic慢
      1. 需要初始解：通常需要Tutte或Harmonic作为初始值
      1. 可能不收敛：在某些情况下可能陷入局部最优

对比总结：

方法 能量函数 优化目标 计算复杂度 适用场景
Tutte $E = \sum |u_i - u_j|^2$ 均匀分布 O(n) 线性 简单模型，需要稳定性
Harmonic $E = \sum w_{ij} |u_i - u_j|^2$ 共形映射 O(n) 线性 需要角度保持
ARAP $E = \sum |(u_i - u_j) - R_i(v_i - v_j)|^2$ 局部刚体保持 O(n·iter) 迭代 复杂模型，需要低失真

📌 注：ARAP是现代参数化算法中的主流方法，在游戏引擎和建模软件中广泛应用，特别适合需要高质量UV展开的场景

对于简单几何体，可以使用数学映射：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

// 1.球面映射
UVCoord sphereMapping(const Vector3& position, const Vector3& center) {
    Vector3 dir = (position - center).normalized();
    float u = 0.5f + atan2(dir.z, dir.x) / (2.0f * PI);
    float v = 0.5f - asin(dir.y) / PI;
    return {u, v};
}

// 2.圆柱映射
UVCoord cylinderMapping(const Vector3& position) {
    float u = atan2(position.z, position.x) / (2.0f * PI) + 0.5f;
    float v = position.y;  // 需要根据模型范围归一化
    return {u, v};
}

// 3.平面映射
UVCoord planarMapping(const Vector3& position, const Vector3& normal) {
    // 投影到垂直于normal的平面
    Vector3 uAxis = chooseOrthogonal(normal);
    Vector3 vAxis = normal.cross(uAxis);
    
    float u = position.dot(uAxis);
    float v = position.dot(vAxis);
    // 归一化到[0,1]
    return {normalize(u), normalize(v)};
}

利用libigl实现Tutte和harmonic，以及ARAP算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

#include <igl/read_triangle_mesh.h>
#include <igl/write_triangle_mesh.h>
#include <igl/boundary_loop.h>
#include <igl/map_vertices_to_circle.h>
#include <igl/harmonic.h>
#include <igl/arap.h>
#include <Eigen/Core>
#include <iostream>

using namespace Eigen;
using namespace std;

int main(int argc, char *argv[])
{
    if(argc < 2)
    {
        cout << "Usage: " << argv[0] << " input_mesh.obj" << endl;
        return -1;
    }

    // ============================
    // 1. 读取网格
    // ============================
    MatrixXd V;
    MatrixXi F;
    if(!igl::read_triangle_mesh(argv[1], V, F))
    {
        cerr << "Failed to read mesh " << argv[1] << endl;
        return -1;
    }
    cout << "Mesh loaded: " << V.rows() << " vertices, " << F.rows() << " faces" << endl;

    // ============================
    // 2. 找边界并映射到单位圆（固定边界）
    // ============================
    VectorXi bnd;
    igl::boundary_loop(F, bnd);

    MatrixXd bnd_uv;
    igl::map_vertices_to_circle(V, bnd, bnd_uv);

    // ============================
    // 3. Tutte embedding（均匀权重）
    // ============================
    MatrixXd uv_tutte;
    igl::harmonic(V, F, bnd, bnd_uv, 1, uv_tutte); // 1 = uniform weight
    igl::write_triangle_mesh("uv_tutte.obj", uv_tutte, F);
    cout << "Tutte embedding saved to uv_tutte.obj" << endl;

    // ============================
    // 4. Harmonic mapping（cotangent权重）
    // ============================
    MatrixXd uv_harmonic;
    igl::harmonic(V, F, bnd, bnd_uv, 2, uv_harmonic); // 2 = cotangent weight
    igl::write_triangle_mesh("uv_harmonic.obj", uv_harmonic, F);
    cout << "Harmonic mapping saved to uv_harmonic.obj" << endl;

    // ============================
    // 5. ARAP 参数化
    // ============================
    MatrixXd uv_arap = uv_harmonic; // 用 Harmonic 初始化
    igl::ARAPData arap_data;
    int dim = 2; // 二维参数化
    igl::ARAPPrecomputation(V, F, dim, bnd, arap_data);

    int max_iter = 50;
    for(int i=0; i<max_iter; i++)
    {
        igl::ARAPStep(uv_arap, arap_data);
    }

    igl::write_triangle_mesh("uv_arap.obj", uv_arap, F);
    cout << "ARAP parameterization saved to uv_arap.obj" << endl;

    cout << "All done!" << endl;
    return 0;
}

2.2.3.2 基于边的展开（Edge-based Unfolding）

核心思想：展开时候，允许在“边”上切开网格。每条边可以标记为：连续边和UV接缝（seam）。接缝边在 UV 空间中会被“断开”。即，原始的网格时一个连通的曲面，在若干条边上“剪开”，把曲面变成一个或者多个拓扑盘，再映射到2D的平面上。这种思想可以保证三角形再UV展开中不发生翻转，易于受到控制，但是同时也可能因为多个接缝，导致UV被切割为多个“岛”（区域块）。

通常方法：

这是一份关于 LSCM（Least Squares Conformal Maps，最小二乘共形映射） 的深度解析，采用与你提供的 ARAP 风格一致的排版，突出核心逻辑与数学之美。

⭐ LSCM（Least Squares Conformal Maps）参数化

内容：LSCM 是一种基于共形（Conformal）几何的参数化方法。其核心思想是最小化角度畸变。与 ARAP 的局部刚性不同，LSCM 允许局部区域发生均匀的缩放，但要求保持形状的角度不变（即满足柯西-黎曼方程）。它是目前工业界（如 Blender, Maya）最常用的 UV 展开算法之一。

原理：

  • 共形条件：对于一个映射 $f\left(x,y\right)=u+iv$ ，如果它是共形的，则必须满足柯西-黎曼方程：

    \[\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},\frac{\partial u}{\partial y}=−\frac{\partial v}{\partial x}\]

  • 能量函数：LSCM 衡量每个三角形从 3D 到 2D 映射时偏离共形条件的程度：

    \[E_{\text{LSCM}} = \sum_{T \in \text{Faces}} \text{Area}(T) \cdot \| \nabla u - \nabla v^{\bot} \|^2\]

    其中：

    • $u,v$ 是顶点的 2D 参数坐标。

    • $\nabla u,\nabla v$ 是在三角形面上的坐标梯度。

    • 该能量函数是二次型的，可以转化为求解一个大型稀疏线性方程组 $Ax=b$ 。

  • 自由边界：与 Tutte 映射必须固定边界到凸多边形不同，LSCM 不需要固定所有边界点。只需固定至少两个顶点（以消除平移、旋转和缩放的自由度），边界会自动寻找最优形状。

算法流程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

// LSCM参数化伪代码
void lscmParameterization(const Mesh& mesh, UVMap& uvMap) {
    // 1. 选取两个锚点以防止模型平移和缩放（通常选距离最远的两个边界点）
    setupConstraints(mesh, uvMap);

    // 2. 构建线性系统矩阵 M
    // M 是由每个三角形的几何关系（面积、边长）构成的系数矩阵
    SparseMatrix M = buildLSCMMatrix(mesh);

    // 3. 求解线性方程组
    // 由于是最小二乘问题，最终转化为求解 (M^T * M) x = b
    // 或者直接构造满足共形条件的线性约束方程组
    solveSparseLinearSystem(M, uvMap);

    // 4. 归一化结果
    normalizeUV(uvMap);
}

// 构建单个三角形的共形约束贡献
void addTriangleContribution(Triangle& T, SparseMatrix& A) {
    // 计算三角形在局部坐标系下的坐标 (x1,y1), (x2,y2), (x3,y3)
    // 根据柯西-黎曼方程的离散形式，填充矩阵 A 的对应位置
    // A * [u1, v1, u2, v2, u3, v3]^T = 0
    float area = T.area();
    // ... 填充梯度算子相关的系数 ...
}

优缺点：

  • 优点：
    1. 角度保持：能完美保持纹理的正交性，避免拉伸感。
    1. 自由边界：边界形状由内部几何自然导出，不会像 Tutte 那样在边缘产生剧烈挤压。
    1. 计算高效：只需解一次线性方程组，无需像 ARAP 那样迭代，速度极快。
    1. 全局最优：能量函数是凸的，保证能找到全局最小值。
  • 缺点：
    1. 面积失真：为了保持角度，某些区域可能会被放大或缩小（缩放因子不一致）。
    1. 容易重叠：对于极其复杂的流形或存在较大曲率的闭合模型，UV 可能会发生自交（Overlap）。
    1. 依赖切口：对于闭合模型，必须手动设置合适的切口（Seams）才能获得好的效果。

用libigl实现lscm算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

#include <igl/read_triangle_mesh.h>
#include <igl/boundary_loop.h>
#include <igl/harmonic.h>
#include <igl/lscm.h>
#include <igl/opengl/glfw/Viewer.h>

#include <Eigen/Core>
#include <iostream>
#include <cmath>

int main()
{
    Eigen::MatrixXd V;
    Eigen::MatrixXi F;
    igl::read_triangle_mesh("input.obj", V, F);

    // ===============================
    // Step 1: boundary loop
    // ===============================
    Eigen::VectorXi bnd;
    igl::boundary_loop(F, bnd);

    // ===============================
    // Step 2: boundary -> unit circle
    // ===============================
    int nb = bnd.size();
    Eigen::MatrixXd bnd_uv(nb, 2);

    for (int i = 0; i < nb; ++i)
    {
        double t = 2.0 * M_PI * i / nb;
        bnd_uv(i, 0) = std::cos(t);
        bnd_uv(i, 1) = std::sin(t);
    }

    // ===============================
    // Step 3: Tutte (harmonic)
    // ===============================
    Eigen::MatrixXd UV_init;
    igl::harmonic(V, F, bnd, bnd_uv, 1, UV_init);

    // ===============================
    // Step 4: LSCM constraints
    // ===============================
    Eigen::VectorXi b(2);
    Eigen::MatrixXd bc(2, 2);

    b << bnd(0), bnd(nb / 2);
    bc.row(0) = UV_init.row(b(0));
    bc.row(1) = UV_init.row(b(1));

    // ===============================
    // Step 5: LSCM refine
    // ===============================
    Eigen::MatrixXd UV;
    igl::lscm(V, F, b, bc, UV);

    // ===============================
    // Step 6: visualize
    // ===============================
    igl::opengl::glfw::Viewer viewer;
    viewer.data().set_mesh(V, F);
    viewer.data().set_uv(UV);
    viewer.data().show_texture = true;
    viewer.launch();
}
⭐ ABF / ABF++（Angle-Based Flattening）参数化

内容：ABF（Angle-Based Flattening）是一种基于角度优化的参数化方法，由Sheffer和de Sturler在2001年提出。其核心思想是直接优化三角形内角，而不是优化顶点位置，从而在参数化过程中最小化角度失真。ABF++是ABF的改进版本，解决了原算法的一些数值稳定性问题，并提高了计算效率。

原理：

  • 角度约束：对于每个三角形，其内角之和必须满足： \(\alpha_i + \beta_i + \gamma_i = \pi\)

    其中 $\alpha_i, \beta_i, \gamma_i$ 是三角形 $i$ 的三个内角。

  • 角度有效性约束：每个内角必须为正： \(\alpha_i > 0, \quad \beta_i > 0, \quad \gamma_i > 0\)

  • 顶点角度约束：对于内部顶点，其周围所有三角形的角度之和必须为 $2\pi$： \(\sum_{j \in N(i)} \theta_{ij} = 2\pi\)

    其中 $N(i)$ 是顶点 $i$ 周围的三角形集合，$\theta_{ij}$ 是三角形 $j$ 在顶点 $i$ 处的角度。

  • 边界顶点约束：对于边界顶点，角度之和为 $\pi$（如果顶点在边界上）： \(\sum_{j \in N(i)} \theta_{ij} = \pi \quad (\text{边界顶点})\)

  • 能量函数：ABF最小化角度与原始3D网格角度的偏差： \(E_{\text{ABF}} = \sum_{i=1}^{n} \sum_{k=1}^{3} w_{ik} (\alpha_{ik} - \bar{\alpha}_{ik})^2\)

    其中：

    • $\alpha_{ik}$ 是参数化后三角形 $i$ 的第 $k$ 个角度
    • $\bar{\alpha}_{ik}$ 是原始3D网格中对应的角度
    • $w_{ik}$ 是权重（通常与三角形面积相关）

  • 优化问题：ABF将参数化问题转化为一个约束优化问题： \(\min_{\alpha} E_{\text{ABF}}(\alpha)\)

    约束条件：

    • 三角形内角和约束：$\alpha_i + \beta_i + \gamma_i = \pi$
    • 顶点角度约束：$\sum_{j \in N(i)} \theta_{ij} = 2\pi$（内部顶点）
    • 角度有效性：$\alpha_i > 0, \beta_i > 0, \gamma_i > 0$

算法流程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

// ABF参数化伪代码
void abfParameterization(const Mesh& mesh, UVMap& uvMap) {
    // 1. 初始化：从原始3D网格提取角度
    std::vector<double> targetAngles = extract3DAngles(mesh);
    
    // 2. 构建约束系统
    //    - 三角形内角和约束
    //    - 顶点角度约束（内部顶点 = 2π，边界顶点 = π）
    //    - 角度有效性约束（> 0）
    ConstraintSystem constraints = buildConstraintSystem(mesh);
    
    // 3. 求解约束优化问题
    //    使用拉格朗日乘数法或内点法
    std::vector<double> optimizedAngles = solveConstrainedOptimization(
        targetAngles, constraints
    );
    
    // 4. 从角度重建UV坐标
    //    给定角度，可以唯一确定三角形的形状（除了缩放和平移）
    reconstructUVFromAngles(mesh, optimizedAngles, uvMap);
    
    // 5. 归一化到[0,1]范围
    normalizeUV(uvMap);
}

// ABF++改进：使用对数空间优化提高数值稳定性
void abfPlusPlusParameterization(const Mesh& mesh, UVMap& uvMap) {
    // 1. 在对数空间中优化角度（避免角度为负的问题）
    std::vector<double> logAngles = logSpaceOptimization(mesh);
    
    // 2. 使用更稳定的数值方法求解
    //    - 改进的线性系统求解器
    //    - 更好的初始值选择
    std::vector<double> optimizedAngles = stableSolve(logAngles, mesh);
    
    // 3. 重建UV坐标
    reconstructUVFromAngles(mesh, optimizedAngles, uvMap);
    normalizeUV(uvMap);
}

// 从角度重建UV坐标
void reconstructUVFromAngles(
    const Mesh& mesh,
    const std::vector<double>& angles,
    UVMap& uvMap
) {
    // 方法1：使用正弦定理
    // 对于三角形ABC，已知角度和一条边，可以计算其他边
    for (const auto& triangle : mesh.triangles) {
        double alpha = angles[triangle.angleA];
        double beta = angles[triangle.angleB];
        double gamma = angles[triangle.angleC];
        
        // 使用正弦定理：a/sin(α) = b/sin(β) = c/sin(γ)
        // 给定一个边的长度，可以计算其他边
        double edgeLength = computeEdgeLength(triangle, angles);
        
        // 从边长度和角度重建三角形形状
        reconstructTriangle(triangle, edgeLength, alpha, beta, gamma, uvMap);
    }
    
    // 方法2：使用局部坐标系逐步构建
    // 从一个三角形开始，逐步添加相邻三角形
    buildUVIncrementally(mesh, angles, uvMap);
}

ABF vs ABF++ 对比：

特性 ABF ABF++
数值稳定性 中等，可能出现角度为负 高，使用对数空间优化
计算效率 较慢 更快，改进的求解器
初始值敏感性 对初始值敏感 更鲁棒
约束处理 标准拉格朗日乘数法 改进的约束处理
适用场景 简单到中等复杂度模型 复杂模型，大规模网格

优缺点：

  • 优点：
      1. 角度优化：直接优化角度，能精确控制角度失真
      1. 无翻转保证：通过角度约束，理论上可以避免三角形翻转
      1. 高质量结果：对于需要精确角度保持的应用（如纹理映射），效果优秀
      1. 数学严谨：基于严格的几何约束，理论基础扎实
  • 缺点：
      1. 计算复杂：需要求解大型约束优化问题，计算开销大
      1. 数值稳定性：原ABF算法在某些情况下可能出现数值问题（ABF++已改进）
      1. 面积失真：专注于角度优化，可能牺牲面积保持
      1. 边界处理：边界顶点的角度约束可能限制参数化的灵活性

算法对比总结：

方法 优化目标 约束类型 计算复杂度 适用场景
LSCM 共形能量（角度） 线性约束 O(n) 线性 快速共形映射
ABF 角度偏差 非线性约束 O(n²) 或更高 精确角度控制
ABF++ 角度偏差（对数空间） 改进的非线性约束 O(n²) 但更稳定 复杂模型，高精度需求
ARAP 局部刚体保持 迭代优化 O(n·iter) 低失真参数化

📌 注：ABF/ABF++特别适合需要精确角度保持的应用，如CAD建模、工程制图等。对于游戏和实时渲染，LSCM和ARAP通常更实用，因为它们在质量和速度之间有更好的平衡。

用libigl实现ABF算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#include <igl/read_triangle_mesh.h>
#include <igl/abf_plus_plus.h>
#include <igl/opengl/glfw/Viewer.h>

#include <Eigen/Core>
#include <iostream>

int main()
{
    Eigen::MatrixXd V;
    Eigen::MatrixXi F;

    igl::read_triangle_mesh("input.obj", V, F);

    Eigen::MatrixXd UV;

    if (!igl::abf_plus_plus(V, F, UV))
    {
        std::cerr << "ABF++ failed!" << std::endl;
        return -1;
    }

    igl::opengl::glfw::Viewer viewer;
    viewer.data().set_mesh(V, F);
    viewer.data().set_uv(UV);
    viewer.data().show_texture = true;
    viewer.launch();
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

// 简化的UV展开伪代码
class UVUnwrapper {
public:
    // 基于切割边的UV展开
    void unwrapMesh(const Mesh& mesh, UVMap& uvMap) {
        // 1. 选择切割边（seam edges），将网格分割成可展开的片
        std::vector<Edge> seamEdges = findSeamEdges(mesh);
        
        // 2. 将网格分割成多个chart（可展开的连通区域）
        std::vector<Chart> charts = splitIntoCharts(mesh, seamEdges);
        
        // 3. 对每个chart进行参数化（如LSCM - Least Squares Conformal Maps）
        for (auto& chart : charts) {
            parameterizeChart(chart);
        }
        
        // 4. 在UV空间中排列各个chart，最小化浪费空间
        packCharts(charts, uvMap);
        
        // 5. 更新网格的UV坐标
        updateMeshUVs(mesh, uvMap);
    }
    
private:
    // 查找切割边（边界或需要切割的边）
    std::vector<Edge> findSeamEdges(const Mesh& mesh) {
        std::vector<Edge> seams;
        // 实现边查找逻辑
        // 通常选择最短路径或基于网格拓扑
        return seams;
    }
    
    // LSCM参数化（最小二乘共形映射）
    void parameterizeChart(Chart& chart) {
        // 构建线性系统：最小化角度失真
        // 求解：argmin ||Lx - b||²
        // 其中L是拉普拉斯算子，x是UV坐标
        Eigen::SparseMatrix<double> L = buildLaplacian(chart);
        Eigen::VectorXd b = buildRHS(chart);
        Eigen::VectorXd uv = solveLinearSystem(L, b);
        
        // 更新chart的UV坐标
        updateChartUVs(chart, uv);
    }
    
    // Chart打包（在UV空间中排列）
    void packCharts(std::vector<Chart>& charts, UVMap& uvMap) {
        // 1. 计算每个chart的边界框
        // 2. 使用装箱算法（如Skyline算法）排列charts
        // 3. 确保不重叠且最小化空白区域
        // 4. 归一化到[0,1]范围
    }
};

三、投影采样算法

3.1 光线投射采样（Ray Casting）

最常用的投影方法是光线投射：从低精度模型表面向高精度模型发射光线进行采样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145

// 光线投射采样核心算法
class TextureBaker {
public:
    // 烘焙光照贴图
    void bakeLightmap(
        const Mesh& highPolyMesh,
        const Mesh& lowPolyMesh,
        const UVMap& uvMap,
        int textureWidth,
        int textureHeight,
        Texture& lightmap
    ) {
        // 初始化纹理
        lightmap.resize(textureWidth, textureHeight);
        
        // 对每个纹理像素进行采样
        for (int y = 0; y < textureHeight; ++y) {
            for (int x = 0; x < textureWidth; ++x) {
                // UV坐标 [0,1]
                float u = (x + 0.5f) / textureWidth;
                float v = (y + 0.5f) / textureHeight;
                
                // 1. 从UV坐标找到对应的三角形和重心坐标
                TriangleInfo triInfo = findTriangleAtUV(lowPolyMesh, uvMap, u, v);
                
                if (!triInfo.valid) continue;
                
                // 2. 计算三维表面点位置和法线
                Vector3 surfacePos = interpolatePosition(
                    triInfo.triangle, triInfo.barycentric
                );
                Vector3 surfaceNormal = interpolateNormal(
                    triInfo.triangle, triInfo.barycentric
                );
                
                // 3. 从表面点向高精度模型投射光线
                Vector3 rayOrigin = surfacePos + surfaceNormal * 0.01f;  // 轻微偏移
                Vector3 rayDir = -surfaceNormal;
                
                // 4. 计算光照值（采样高精度模型的几何）
                Color lightValue = sampleLighting(
                    highPolyMesh, rayOrigin, rayDir, surfaceNormal
                );
                
                // 5. 存储到纹理
                lightmap.setPixel(x, y, lightValue);
            }
        }
    }
    
private:
    // 查找UV坐标对应的三角形
    struct TriangleInfo {
        Triangle triangle;
        Vector3 barycentric;  // 重心坐标
        bool valid;
    };
    
    TriangleInfo findTriangleAtUV(
        const Mesh& mesh,
        const UVMap& uvMap,
        float u, float v
    ) {
        TriangleInfo info = {Triangle(), Vector3(), false};
        
        // 遍历所有三角形，查找包含该UV坐标的三角形
        for (const auto& triangle : mesh.triangles) {
            Vector3 uv0 = uvMap.getUV(triangle.v0);
            Vector3 uv1 = uvMap.getUV(triangle.v1);
            Vector3 uv2 = uvMap.getUV(triangle.v2);
            
            // 使用重心坐标判断点是否在三角形内
            Vector3 bary = computeBarycentric(
                Vector2(u, v),
                Vector2(uv0.u, uv0.v),
                Vector2(uv1.u, uv1.v),
                Vector2(uv2.u, uv2.v)
            );
            
            // 检查重心坐标是否有效（所有分量>=0且和=1）
            if (bary.x >= 0 && bary.y >= 0 && bary.z >= 0 &&
                fabs(bary.x + bary.y + bary.z - 1.0f) < 1e-5) {
                info.triangle = triangle;
                info.barycentric = bary;
                info.valid = true;
                return info;
            }
        }
        
        return info;
    }
    
    // 计算重心坐标
    Vector3 computeBarycentric(
        const Vector2& p,
        const Vector2& a,
        const Vector2& b,
        const Vector2& c
    ) {
        Vector2 v0 = c - a;
        Vector2 v1 = b - a;
        Vector2 v2 = p - a;
        
        float dot00 = v0.dot(v0);
        float dot01 = v0.dot(v1);
        float dot02 = v0.dot(v2);
        float dot11 = v1.dot(v1);
        float dot12 = v1.dot(v2);
        
        float invDenom = 1.0f / (dot00 * dot11 - dot01 * dot01);
        float u = (dot11 * dot02 - dot01 * dot12) * invDenom;
        float v = (dot00 * dot12 - dot01 * dot02) * invDenom;
        
        return Vector3(1.0f - u - v, v, u);
    }
    
    // 采样光照
    Color sampleLighting(
        const Mesh& highPolyMesh,
        const Vector3& rayOrigin,
        const Vector3& rayDir,
        const Vector3& surfaceNormal
    ) {
        // 射线与高精度网格的交点
        IntersectionResult intersection = rayMeshIntersect(
            highPolyMesh, rayOrigin, rayDir
        );
        
        if (!intersection.hit) {
            // 没有命中，使用默认值或环境光
            return Color(0.1f, 0.1f, 0.1f);  // 环境光
        }
        
        // 使用Phong光照模型计算光照
        Vector3 hitNormal = intersection.normal;
        Vector3 hitPos = intersection.position;
        
        // 简化光照计算（实际可以使用更复杂的模型）
        Color ambient = Color(0.2f, 0.2f, 0.2f);
        Color diffuse = computeDiffuseLighting(hitPos, hitNormal);
        Color specular = computeSpecularLighting(hitPos, hitNormal, surfaceNormal);
        
        return ambient + diffuse + specular;
    }
};

3.2 距离场采样（Distance Field）

对于某些类型的烘焙（如法线贴图），可以使用距离场方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92

// 距离场法线贴图烘焙
class NormalMapBaker {
public:
    void bakeNormalMap(
        const Mesh& highPolyMesh,
        const Mesh& lowPolyMesh,
        const UVMap& uvMap,
        int textureWidth,
        int textureHeight,
        float sampleRadius,
        Texture& normalMap
    ) {
        normalMap.resize(textureWidth, textureHeight);
        
        // 预计算高精度网格的距离场（可选，用于加速）
        DistanceField distanceField(highPolyMesh);
        
        for (int y = 0; y < textureHeight; ++y) {
            for (int x = 0; x < textureWidth; ++x) {
                float u = (x + 0.5f) / textureWidth;
                float v = (y + 0.5f) / textureHeight;
                
                TriangleInfo triInfo = findTriangleAtUV(lowPolyMesh, uvMap, u, v);
                if (!triInfo.valid) continue;
                
                Vector3 surfacePos = interpolatePosition(
                    triInfo.triangle, triInfo.barycentric
                );
                Vector3 surfaceNormal = interpolateNormal(
                    triInfo.triangle, triInfo.barycentric
                );
                
                // 在切空间中采样高精度几何
                Vector3 tangent, bitangent;
                computeTangentSpace(
                    triInfo.triangle, triInfo.barycentric, tangent, bitangent
                );
                
                // 使用有限差分计算法线贴图
                Vector3 normal = computeNormalFromDistanceField(
                    distanceField, surfacePos, surfaceNormal,
                    tangent, bitangent, sampleRadius
                );
                
                // 转换到切空间并存储为RGB
                Vector3 tangentSpaceNormal = worldToTangentSpace(
                    normal, surfaceNormal, tangent, bitangent
                );
                
                // 法线从[-1,1]映射到[0,1]
                Color normalColor(
                    0.5f + 0.5f * tangentSpaceNormal.x,
                    0.5f + 0.5f * tangentSpaceNormal.y,
                    0.5f + 0.5f * tangentSpaceNormal.z
                );
                
                normalMap.setPixel(x, y, normalColor);
            }
        }
    }
    
private:
    // 从距离场计算法线（使用有限差分）
    Vector3 computeNormalFromDistanceField(
        const DistanceField& df,
        const Vector3& pos,
        const Vector3& normal,
        const Vector3& tangent,
        const Vector3& bitangent,
        float radius
    ) {
        float eps = 0.001f;
        
        // 在切平面上的采样点
        Vector3 offsetU = tangent * radius;
        Vector3 offsetV = bitangent * radius;
        
        // 计算高度差异（使用距离场）
        float h0 = df.sample(pos);
        float hU = df.sample(pos + offsetU);
        float hV = df.sample(pos + offsetV);
        
        // 有限差分计算梯度
        Vector3 gradient(
            (hU - h0) / radius,
            (hV - h0) / radius,
            1.0f
        );
        
        return gradient.normalized();
    }
};

四、环境遮蔽（AO）烘焙

环境遮蔽（Ambient Occlusion）模拟表面点被周围几何体遮挡的程度，是增强模型视觉深度的重要技术。

4.1 AO计算原理

AO值的计算公式：

\[AO(p) = \frac{1}{\pi} \int_{\Omega} V(p, \omega) \cos(\theta) d\omega\]

其中：

  • $p$ 是表面点
  • $\Omega$ 是上半球方向
  • $V(p, \omega)$ 是可见性函数（1表示可见，0表示被遮挡）
  • $\theta$ 是方向与法线的夹角
  • $\cos(\theta)$ 是权重函数

4.2 AO烘焙实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118

// 环境遮蔽烘焙
class AOBaker {
public:
    void bakeAO(
        const Mesh& highPolyMesh,
        const Mesh& lowPolyMesh,
        const UVMap& uvMap,
        int textureWidth,
        int textureHeight,
        int numSamples,
        float sampleRadius,
        Texture& aoMap
    ) {
        aoMap.resize(textureWidth, textureHeight);
        
        // 构建空间加速结构（如BVH）
        BVHTree bvh(highPolyMesh);
        
        for (int y = 0; y < textureHeight; ++y) {
            for (int x = 0; x < textureWidth; ++x) {
                float u = (x + 0.5f) / textureWidth;
                float v = (y + 0.5f) / textureHeight;
                
                TriangleInfo triInfo = findTriangleAtUV(lowPolyMesh, uvMap, u, v);
                if (!triInfo.valid) continue;
                
                Vector3 surfacePos = interpolatePosition(
                    triInfo.triangle, triInfo.barycentric
                );
                Vector3 surfaceNormal = interpolateNormal(
                    triInfo.triangle, triInfo.barycentric
                );
                
                // 蒙特卡洛采样计算AO
                float ao = computeAO(
                    bvh, surfacePos, surfaceNormal,
                    numSamples, sampleRadius
                );
                
                // 存储AO值（单通道）
                aoMap.setPixel(x, y, Color(ao, ao, ao));
            }
        }
    }
    
private:
    // 计算单点的AO值（蒙特卡洛方法）
    float computeAO(
        const BVHTree& bvh,
        const Vector3& pos,
        const Vector3& normal,
        int numSamples,
        float radius
    ) {
        int occludedCount = 0;
        
        // 在上半球进行采样
        for (int i = 0; i < numSamples; ++i) {
            // 生成随机方向（在法线周围的半球内）
            Vector3 sampleDir = sampleHemisphere(normal);
            
            // 偏移起点，避免自相交
            Vector3 rayOrigin = pos + normal * 0.001f;
            Vector3 rayDir = sampleDir;
            float rayLength = radius;
            
            // 射线检测
            IntersectionResult hit = bvh.intersect(rayOrigin, rayDir, rayLength);
            
            if (hit.hit) {
                // 被遮挡，使用距离衰减权重
                float distance = hit.distance;
                float weight = 1.0f - (distance / radius);
                occludedCount += weight;
            }
        }
        
        // AO值 = 1 - 被遮挡的加权平均
        float ao = 1.0f - (occludedCount / numSamples);
        return ao;
    }
    
    // 在法线周围的半球内采样方向（余弦加权）
    Vector3 sampleHemisphere(const Vector3& normal) {
        // 生成随机方向（使用余弦分布）
        float u1 = randomFloat();
        float u2 = randomFloat();
        
        // 在单位圆盘上采样
        float r = sqrt(u1);
        float theta = 2.0f * PI * u2;
        
        float x = r * cos(theta);
        float y = r * sin(theta);
        float z = sqrt(1.0f - u1);  // 余弦分布
        
        // 构建切空间基
        Vector3 tangent, bitangent;
        buildOrthogonalBasis(normal, tangent, bitangent);
        
        // 转换到世界空间
        return (tangent * x + bitangent * y + normal * z).normalized();
    }
    
    // 构建正交基（用于切空间转换）
    void buildOrthogonalBasis(
        const Vector3& normal,
        Vector3& tangent,
        Vector3& bitangent
    ) {
        // 选择一个与法线不平行的向量
        Vector3 up = (fabs(normal.y) < 0.9f) ?
            Vector3(0, 1, 0) : Vector3(1, 0, 0);
        
        tangent = normal.cross(up).normalized();
        bitangent = normal.cross(tangent).normalized();
    }
};

五、法线贴图烘焙

法线贴图（Normal Map）存储高精度模型的表面法线信息，用于在低精度模型上呈现细节。

5.1 法线贴图原理

法线贴图将法线向量编码为RGB颜色：

  • R通道：切空间中法线的X分量
  • G通道：切空间中法线的Y分量
  • B通道：切空间中法线的Z分量

法线从$[-1, 1]$范围映射到$[0, 255]$（或$[0, 1]$浮点范围）。

5.2 法线贴图烘焙实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136

// 法线贴图烘焙
class NormalMapBaker {
public:
    void bakeNormalMap(
        const Mesh& highPolyMesh,
        const Mesh& lowPolyMesh,
        const UVMap& uvMap,
        int textureWidth,
        int textureHeight,
        float rayDistance,
        Texture& normalMap
    ) {
        normalMap.resize(textureWidth, textureHeight);
        BVHTree bvh(highPolyMesh);
        
        for (int y = 0; y < textureHeight; ++y) {
            for (int x = 0; x < textureWidth; ++x) {
                float u = (x + 0.5f) / textureWidth;
                float v = (y + 0.5f) / textureHeight;
                
                TriangleInfo triInfo = findTriangleAtUV(lowPolyMesh, uvMap, u, v);
                if (!triInfo.valid) continue;
                
                Vector3 surfacePos = interpolatePosition(
                    triInfo.triangle, triInfo.barycentric
                );
                Vector3 surfaceNormal = interpolateNormal(
                    triInfo.triangle, triInfo.barycentric
                );
                
                // 计算切空间基
                Vector3 tangent, bitangent;
                computeTangentSpace(
                    triInfo.triangle, triInfo.barycentric, tangent, bitangent
                );
                
                // 从高精度模型采样法线
                Vector3 sampledNormal = sampleHighPolyNormal(
                    bvh, surfacePos, surfaceNormal, rayDistance
                );
                
                // 转换到切空间
                Vector3 tangentSpaceNormal = worldToTangentSpace(
                    sampledNormal, surfaceNormal, tangent, bitangent
                );
                
                // 归一化（确保在单位球上）
                tangentSpaceNormal = tangentSpaceNormal.normalized();
                
                // 映射到[0,1]并存储
                Color normalColor(
                    0.5f + 0.5f * tangentSpaceNormal.x,
                    0.5f + 0.5f * tangentSpaceNormal.y,
                    0.5f + 0.5f * tangentSpaceNormal.z
                );
                
                normalMap.setPixel(x, y, normalColor);
            }
        }
    }
    
private:
    // 从高精度模型采样法线
    Vector3 sampleHighPolyNormal(
        const BVHTree& bvh,
        const Vector3& surfacePos,
        const Vector3& surfaceNormal,
        float rayDistance
    ) {
        // 沿着法线方向投射射线
        Vector3 rayOrigin = surfacePos + surfaceNormal * 0.001f;
        Vector3 rayDir = -surfaceNormal;  // 向模型内部
        
        IntersectionResult hit = bvh.intersect(rayOrigin, rayDir, rayDistance);
        
        if (hit.hit) {
            // 返回命中点的法线
            return hit.normal;
        } else {
            // 未命中，返回表面法线
            return surfaceNormal;
        }
    }
    
    // 世界空间到切空间转换
    Vector3 worldToTangentSpace(
        const Vector3& worldVec,
        const Vector3& normal,
        const Vector3& tangent,
        const Vector3& bitangent
    ) {
        // 构建变换矩阵（切空间到世界空间）
        Matrix3 TBN(
            tangent.x, bitangent.x, normal.x,
            tangent.y, bitangent.y, normal.y,
            tangent.z, bitangent.z, normal.z
        );
        
        // 逆变换（世界空间到切空间）= 转置（因为正交矩阵）
        return TBN.transpose() * worldVec;
    }
    
    // 计算切空间基向量
    void computeTangentSpace(
        const Triangle& triangle,
        const Vector3& barycentric,
        Vector3& tangent,
        Vector3& bitangent
    ) {
        // 从UV坐标计算切向量
        Vector3 edge1 = triangle.v1.position - triangle.v0.position;
        Vector3 edge2 = triangle.v2.position - triangle.v0.position;
        
        Vector2 deltaUV1 = triangle.v1.uv - triangle.v0.uv;
        Vector2 deltaUV2 = triangle.v2.uv - triangle.v0.uv;
        
        float f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);
        
        tangent = Vector3(
            f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x),
            f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y),
            f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z)
        ).normalized();
        
        bitangent = Vector3(
            f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x),
            f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y),
            f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z)
        ).normalized();
        
        // 使用Gram-Schmidt正交化（处理法线贴图扭曲）
        Vector3 normal = interpolateNormal(triangle, barycentric);
        tangent = (tangent - normal * normal.dot(tangent)).normalized();
        bitangent = normal.cross(tangent);
    }
};

六、光照贴图烘焙

光照贴图（Lightmap）预先计算并存储静态光照信息，是实时渲染中的重要优化技术。

6.1 光照计算模型

常用的光照模型包括：

Phong光照模型：

\[I = I_a k_a + I_d k_d (\mathbf{n} \cdot \mathbf{l}) + I_s k_s (\mathbf{r} \cdot \mathbf{v})^n\]

其中：

  • $I_a, I_d, I_s$：环境光、漫反射光、镜面反射光强度
  • $k_a, k_d, k_s$：材质系数
  • $\mathbf{n}, \mathbf{l}, \mathbf{r}, \mathbf{v}$：法线、光方向、反射方向、视线方向
  • $n$：高光指数

6.2 光照贴图烘焙实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124

// 光照贴图烘焙
class LightmapBaker {
public:
    struct Light {
        Vector3 position;
        Color color;
        float intensity;
        LightType type;  // POINT, DIRECTIONAL, SPOT
    };
    
    void bakeLightmap(
        const Mesh& highPolyMesh,
        const Mesh& lowPolyMesh,
        const UVMap& uvMap,
        const std::vector<Light>& lights,
        int textureWidth,
        int textureHeight,
        Texture& lightmap
    ) {
        lightmap.resize(textureWidth, textureHeight);
        BVHTree bvh(highPolyMesh);
        
        for (int y = 0; y < textureHeight; ++y) {
            for (int x = 0; x < textureWidth; ++x) {
                float u = (x + 0.5f) / textureWidth;
                float v = (y + 0.5f) / textureHeight;
                
                TriangleInfo triInfo = findTriangleAtUV(lowPolyMesh, uvMap, u, v);
                if (!triInfo.valid) continue;
                
                Vector3 surfacePos = interpolatePosition(
                    triInfo.triangle, triInfo.barycentric
                );
                Vector3 surfaceNormal = interpolateNormal(
                    triInfo.triangle, triInfo.barycentric
                );
                
                // 计算该点的总光照
                Color totalLight = Color(0, 0, 0);
                
                // 环境光
                totalLight += computeAmbientLight();
                
                // 对每个光源计算贡献
                for (const auto& light : lights) {
                    Color lightContribution = computeLightContribution(
                        bvh, surfacePos, surfaceNormal, light
                    );
                    totalLight += lightContribution;
                }
                
                // 限制到[0,1]范围
                totalLight.clamp(0.0f, 1.0f);
                lightmap.setPixel(x, y, totalLight);
            }
        }
    }
    
private:
    // 计算单个光源的贡献
    Color computeLightContribution(
        const BVHTree& bvh,
        const Vector3& surfacePos,
        const Vector3& surfaceNormal,
        const Light& light
    ) {
        Vector3 lightDir;
        float lightDistance;
        
        // 计算光方向和距离
        switch (light.type) {
            case POINT:
                lightDir = (light.position - surfacePos);
                lightDistance = lightDir.length();
                lightDir = lightDir.normalized();
                break;
            case DIRECTIONAL:
                lightDir = light.position.normalized();  // 作为方向
                lightDistance = FLT_MAX;
                break;
            case SPOT:
                // 聚光灯处理
                lightDir = (light.position - surfacePos);
                lightDistance = lightDir.length();
                lightDir = lightDir.normalized();
                // 检查角度范围
                break;
        }
        
        // 阴影测试（射线检测）
        Vector3 shadowRayOrigin = surfacePos + surfaceNormal * 0.001f;
        IntersectionResult shadowHit = bvh.intersect(
            shadowRayOrigin, lightDir, lightDistance
        );
        
        if (shadowHit.hit) {
            // 被遮挡，无光照贡献
            return Color(0, 0, 0);
        }
        
        // 计算光照
        float NdotL = std::max(0.0f, surfaceNormal.dot(lightDir));
        if (NdotL <= 0) {
            return Color(0, 0, 0);
        }
        
        // 漫反射
        Color diffuse = light.color * light.intensity * NdotL;
        
        // 距离衰减（点光源）
        if (light.type == POINT) {
            float attenuation = 1.0f / (1.0f + 0.09f * lightDistance +
                                         0.032f * lightDistance * lightDistance);
            diffuse = diffuse * attenuation;
        }
        
        return diffuse;
    }
    
    Color computeAmbientLight() {
        // 简化的环境光
        return Color(0.1f, 0.1f, 0.1f);
    }
};

七、优化技巧

7.1 空间加速结构

为了加速射线检测，可以使用空间加速结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119

// BVH树（Bounding Volume Hierarchy）
class BVHNode {
public:
    AABB boundingBox;
    std::vector<Triangle> triangles;  // 叶子节点
    BVHNode* left;
    BVHNode* right;
};

class BVHTree {
public:
    void build(const Mesh& mesh) {
        std::vector<Triangle> allTriangles = mesh.getAllTriangles();
        root = buildRecursive(allTriangles, 0, allTriangles.size());
    }
    
    IntersectionResult intersect(
        const Vector3& rayOrigin,
        const Vector3& rayDir,
        float maxDistance
    ) const {
        return intersectRecursive(root, rayOrigin, rayDir, maxDistance);
    }
    
private:
    BVHNode* buildRecursive(
        std::vector<Triangle>& triangles,
        int start,
        int end
    ) {
        if (end - start <= 4) {
            // 叶子节点：直接存储三角形
            BVHNode* leaf = new BVHNode();
            for (int i = start; i < end; ++i) {
                leaf->triangles.push_back(triangles[i]);
                leaf->boundingBox.expand(triangles[i].getAABB());
            }
            return leaf;
        }
        
        // 计算所有三角形的包围盒
        AABB bounds;
        for (int i = start; i < end; ++i) {
            bounds.expand(triangles[i].getAABB());
        }
        
        // 选择分割轴（最长轴）
        Vector3 extent = bounds.max - bounds.min;
        int axis = (extent.x > extent.y) ?
            ((extent.x > extent.z) ? 0 : 2) :
            ((extent.y > extent.z) ? 1 : 2);
        
        // 按中位数分割
        int mid = (start + end) / 2;
        std::nth_element(
            triangles.begin() + start,
            triangles.begin() + mid,
            triangles.begin() + end,
            [axis](const Triangle& a, const Triangle& b) {
                return a.getCenter()[axis] < b.getCenter()[axis];
            }
        );
        
        // 递归构建
        BVHNode* node = new BVHNode();
        node->boundingBox = bounds;
        node->left = buildRecursive(triangles, start, mid);
        node->right = buildRecursive(triangles, mid, end);
        
        return node;
    }
    
    IntersectionResult intersectRecursive(
        const BVHNode* node,
        const Vector3& rayOrigin,
        const Vector3& rayDir,
        float maxDistance
    ) const {
        if (!node) return IntersectionResult();
        
        // 射线与包围盒相交测试
        float tMin, tMax;
        if (!node->boundingBox.intersect(rayOrigin, rayDir, tMin, tMax)) {
            return IntersectionResult();
        }
        
        if (node->triangles.empty()) {
            // 内部节点：递归检测
            IntersectionResult leftHit = intersectRecursive(
                node->left, rayOrigin, rayDir, maxDistance
            );
            IntersectionResult rightHit = intersectRecursive(
                node->right, rayOrigin, rayDir, maxDistance
            );
            
            // 返回最近的交点
            if (!leftHit.hit) return rightHit;
            if (!rightHit.hit) return leftHit;
            return (leftHit.distance < rightHit.distance) ? leftHit : rightHit;
        } else {
            // 叶子节点：检测所有三角形
            IntersectionResult closest;
            closest.distance = maxDistance;
            
            for (const auto& triangle : node->triangles) {
                IntersectionResult hit = rayTriangleIntersect(
                    rayOrigin, rayDir, triangle
                );
                if (hit.hit && hit.distance < closest.distance) {
                    closest = hit;
                }
            }
            
            return closest;
        }
    }
    
    BVHNode* root;
};

7.2 多线程加速

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

// 并行烘焙
#include <thread>
#include <vector>

void bakeTextureParallel(
    const Mesh& highPolyMesh,
    const Mesh& lowPolyMesh,
    const UVMap& uvMap,
    int textureWidth,
    int textureHeight,
    Texture& outputTexture
) {
    outputTexture.resize(textureWidth, textureHeight);
    
    int numThreads = std::thread::hardware_concurrency();
    int rowsPerThread = textureHeight / numThreads;
    
    std::vector<std::thread> threads;
    
    for (int t = 0; t < numThreads; ++t) {
        int startRow = t * rowsPerThread;
        int endRow = (t == numThreads - 1) ? textureHeight : (t + 1) * rowsPerThread;
        
        threads.emplace_back([&, startRow, endRow]() {
            // 每个线程处理一部分行
            for (int y = startRow; y < endRow; ++y) {
                for (int x = 0; x < textureWidth; ++x) {
                    // 烘焙逻辑
                    Color color = bakePixel(x, y, ...);
                    outputTexture.setPixel(x, y, color);
                }
            }
        });
    }
    
    // 等待所有线程完成
    for (auto& thread : threads) {
        thread.join();
    }
}

八、应用场景与总结

8.1 应用场景

  1. 游戏开发：将高精度模型的细节烘焙到低精度模型，在保持性能的同时获得高质量视觉效果
  2. 建筑可视化：预计算静态光照，实现快速实时漫游
  3. VR/AR应用：在有限的移动设备性能下实现高质量渲染
  4. 动画制作：将复杂的材质和光照效果烘焙到纹理，简化后期处理

8.2 优势与局限性

优势：

  • 显著提升渲染性能
  • 保持视觉质量
  • 减少运行时计算
  • 支持复杂的全局光照效果

局限性：

  • 纹理内存占用增加
  • 只适用于静态或准静态场景
  • 烘焙过程需要时间
  • UV展开质量直接影响烘焙效果

8.3 最佳实践

  1. UV展开质量：确保UV展开无重叠、扭曲最小、空间利用率高
  2. 纹理分辨率：根据模型大小和屏幕空间占比选择合适的纹理分辨率
  3. 采样质量：使用足够的采样数量（特别是AO），平衡质量和速度
  4. 压缩格式：根据烘焙内容选择合适的纹理压缩格式（如BC5用于法线贴图）
  5. 混合策略：结合静态烘焙和动态光照，获得最佳效果

纹理烘焙是连接高精度建模和实时渲染的重要桥梁，通过合理的算法设计和优化，可以在性能和质量之间找到最佳平衡点。

CATALOG
    FEATURED TAGS
    Optimization Algorithm C++ Machine Learning 最优化理论 最优化算法 机器学习 Data Structure Mathematics 分类算法 数据结构 算法实现 Computer Graphics Examples Geometry 二叉排序树 二叉树 数学原理 数学理论 深度学习 算法 3D Modeling Classification Conjugate Gradient Constrained Optimization Convex Analysis Cross Platform Deep Learning Design Patterns Math Mathematical Theory Newton Method Nonlinear Programming Numerical Computation Quasi-Newton Sorting Steepest Descent Unsupervised Learning Visualization
    FRIENDS