最优化基础——KKT条件

KKT条件（Karush-Kuhn-Tucker条件）是约束优化理论中最重要的最优性条件之一。它提供了在约束条件下判断局部最优解的必要条件，是拉格朗日乘数法的推广。本文将从几何直观出发，深入讲解KKT条件的理论基础、几何意义和实际应用。

一、KKT条件的背景

1.1 从拉格朗日乘数法到KKT条件

在无约束优化问题中，我们通过梯度为零来寻找最优解： $\nabla f(x^*) = 0$

对于等式约束问题： $\begin{align} \min \quad & f(x) \\ \text{s.t.} \quad & h_i(x) = 0, \quad i = 1, \ldots, m \end{align}$

拉格朗日乘数法告诉我们，在最优解处存在乘子 $\lambda_i$ 使得： $\nabla f(x^*) + \sum_{i=1}^m \lambda_i \nabla h_i(x^*) = 0$

KKT条件将这一思想推广到包含不等式约束的一般约束优化问题。

1.2 约束优化问题的标准形式

考虑一般约束优化问题： $\begin{align} \min \quad & f(x) \\ \text{s.t.} \quad & g_i(x) \leq 0, \quad i = 1, \ldots, p \\ & h_j(x) = 0, \quad j = 1, \ldots, q \end{align}$

其中：

$f: \mathbb{R}^n \to \mathbb{R}$ 是目标函数
$g_i: \mathbb{R}^n \to \mathbb{R}$ 是不等式约束函数
$h_j: \mathbb{R}^n \to \mathbb{R}$ 是等式约束函数

二、KKT条件的数学表述

KKT条件的数学表述

2.1 KKT条件的内容

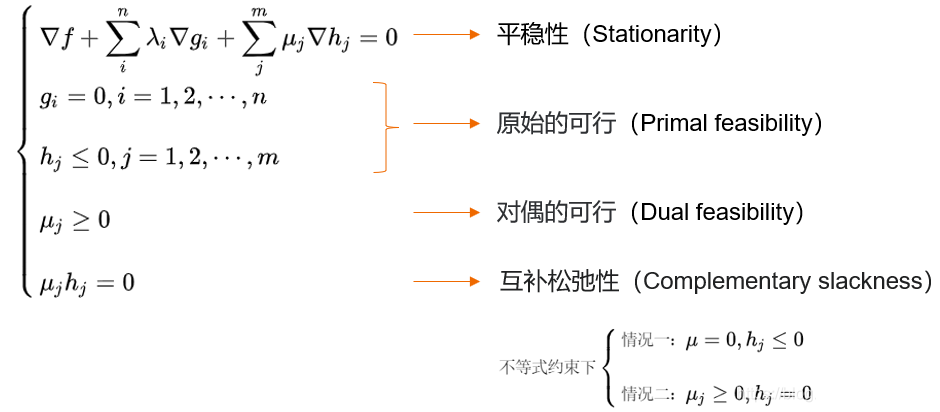
设 $x^*$ 是约束优化问题的局部最优解，且满足线性无关约束条件（LICQ），则存在拉格朗日乘子 $\lambda_i^* \geq 0$ 和 $\nu_j^*$ 使得：

1. 平稳性条件（Stationarity）(驻点条件)： $\nabla f(x^*) + \sum_{i=1}^p \lambda_i^* \nabla g_i(x^*) + \sum_{j=1}^q \nu_j^* \nabla h_j(x^*) = 0$

👉 目标函数的梯度，被约束的“拉力”平衡住了。

2. 原始可行性（Primal Feasibility）： $g_i(x^*) \leq 0, \quad i = 1, \ldots, p$ $h_j(x^*) = 0, \quad j = 1, \ldots, q$

👉 解必须在可行域内。

3. 对偶可行性（Dual Feasibility）： $\lambda_i^* \geq 0, \quad i = 1, \ldots, p$

👉 不等式约束的“罚力度”不能为负。

4. 互补松弛性（Complementary Slackness）： $\lambda_i^* g_i(x^*) = 0, \quad i = 1, \ldots, p$

👉 如果约束没“卡住”（$g_i(x^)<0$），它的乘子$\lambda$必须=0；如果约束正好“贴住”（$g_i(x^)=0$），它的乘子$\lambda$可以> 0。

直观理解就是： 👉 最优点的梯度被一部分约束”抵消”，最终解要么在内部（无约束情况），要么在边界（激活约束起作用.

三、KKT条件的几何意义

3.1 几何直观

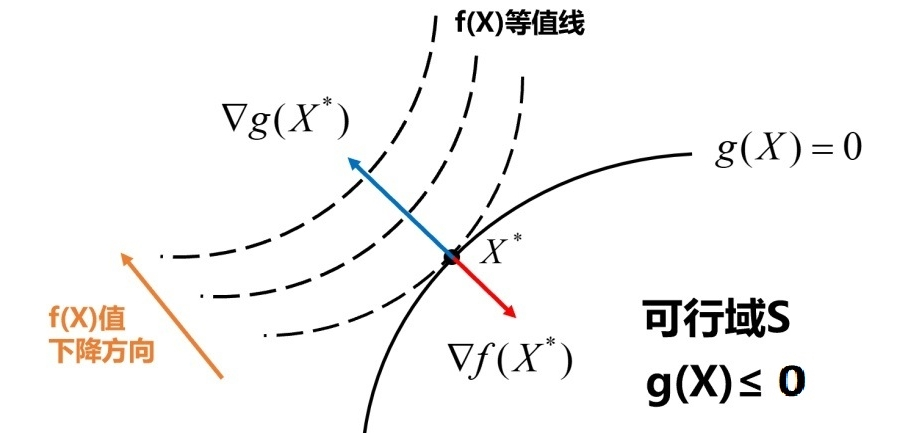
图1：KKT条件单约束情况

kkt条件单约束情况

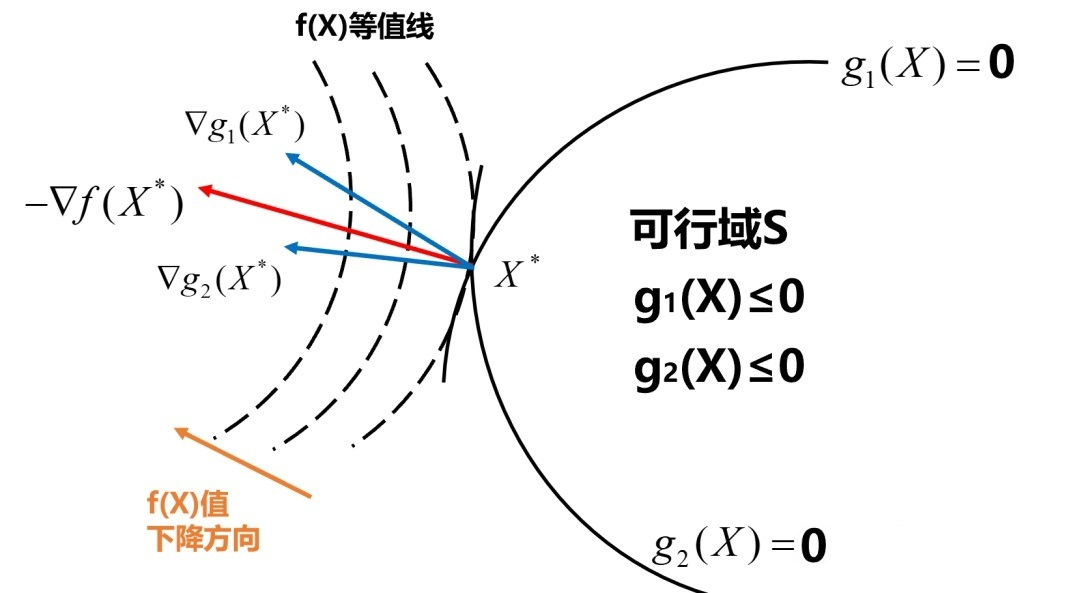
图2：KKT条件多约束情况

kkt条件多约束情况

KKT条件的几何意义可以通过以下方式理解：

在最优解处，目标函数的梯度可以表示为约束函数梯度的非负线性组合。

具体来说：

对于起作用的不等式约束（激活约束）（$g_i(x^*) = 0$），其梯度 $\nabla g_i(x^*)$ 指向可行域外部
对于不起作用的不等式约束（非激活约束）（$g_i(x^*) < 0$），对应的乘子 $\lambda_i^* = 0$
对于等式约束（始终是激活的），梯度 $\nabla h_j(x^*)$ 垂直于约束曲面

3.2 几何解释的数学表述

设 $\mathcal{A}(x^*) = \{i : g_i(x^*) = 0\}$ 为在 $x^*$ 处起作用的约束集合，则KKT条件可以写成：

\[\nabla f(x^*) + \sum_{i \in \mathcal{A}(x^*)} \lambda_i^* \nabla g_i(x^*) + \sum_{j=1}^q \nu_j^* \nabla h_j(x^*) = 0\]

其中 $\lambda_i^* \geq 0$ 对所有 $i \in \mathcal{A}(x^*)$。

四、约束条件（”正则点”）

4.1 线性无关约束条件（LICQ）

定义：在点 $x^*$ 处，所有起作用约束的梯度线性无关，即：线性无关。 $\{\nabla g_i(x^*) : i \in \mathcal{A}(x^*)\} \cup \{\nabla h_j(x^*) : j = 1, \ldots, q\}$

重要性：LICQ是KKT条件成立的必要条件。如果不满足LICQ，KKT条件可能不成立。

4.2 其他约束条件

除了LICQ，还有其他约束条件可以保证KKT条件的成立：

Mangasarian-Fromovitz条件（MFCQ）：比起LICQ稍微弱一些，要求等式约束梯度线性无关，并且在一个方向能“离开”激活约束。
线性独立约束条件（LICQ） ：在点$x*$所有激活的不等式约束的梯度 $\nabla g_i(x^*)$ 和等式约束的梯度$\nabla h_j(x^*)$必须线性无关。
Slater条件（对于凸优化问题）：如果问题是凸的，只要存在一个严格可行点（即$g_i(x) < 0 且h_j(x) = 0$）,则满足正则条件。

五、KKT条件的应用实例

例1：简单的二次规划问题

问题： $\begin{align} \min \quad & f(x_1, x_2) = x_1^2 + x_2^2 \\ \text{s.t.} \quad & g_1(x_1, x_2) = x_1 + x_2 - 1 \leq 0 \\ & g_2(x_1, x_2) = -x_1 \leq 0 \\ & g_3(x_1, x_2) = -x_2 \leq 0 \end{align}$

解：

步骤1：构造拉格朗日函数 $L(x_1, x_2, \lambda_1, \lambda_2, \lambda_3) = x_1^2 + x_2^2 + \lambda_1(x_1 + x_2 - 1) - \lambda_2 x_1 - \lambda_3 x_2$

步骤2：写出KKT条件 $\begin{cases} \frac{\partial L}{\partial x_1} = 2x_1 + \lambda_1 - \lambda_2 = 0 \\ \frac{\partial L}{\partial x_2} = 2x_2 + \lambda_1 - \lambda_3 = 0 \\ x_1 + x_2 - 1 \leq 0, \quad -x_1 \leq 0, \quad -x_2 \leq 0 \\ \lambda_1 \geq 0, \quad \lambda_2 \geq 0, \quad \lambda_3 \geq 0 \\ \lambda_1(x_1 + x_2 - 1) = 0, \quad \lambda_2 x_1 = 0, \quad \lambda_3 x_2 = 0 \end{cases}$

步骤3：分析约束的起作用情况

由于目标函数是 $x_1^2 + x_2^2$，最优解应该在可行域内距离原点最近的点。

情况1：如果 $x_1 > 0, x_2 > 0$，则 $\lambda_2 = \lambda_3 = 0$

如果 $x_1 + x_2 < 1$，则 $\lambda_1 = 0$，得到 $x_1 = x_2 = 0$，但这不满足 $x_1 > 0, x_2 > 0$
如果 $x_1 + x_2 = 1$，则 $\lambda_1 > 0$，得到 $x_1 = x_2 = \frac{1}{2}$

情况2：如果 $x_1 = 0, x_2 > 0$，则 $\lambda_2 \geq 0, \lambda_3 = 0$

如果 $x_2 < 1$，则 $\lambda_1 = 0$，得到 $x_2 = 0$，矛盾
如果 $x_2 = 1$，则 $\lambda_1 > 0$，得到 $x_1 = 0, x_2 = 1$

情况3：如果 $x_1 > 0, x_2 = 0$，类似分析得到 $x_1 = 1, x_2 = 0$

情况4：如果 $x_1 = 0, x_2 = 0$，则 $\lambda_2 \geq 0, \lambda_3 \geq 0$

步骤4：比较目标函数值

$f(0, 0) = 0$
$f(\frac{1}{2}, \frac{1}{2}) = \frac{1}{2}$
$f(0, 1) = 1$
$f(1, 0) = 1$

结论：最优解为 $x^* = (0, 0)$，对应的乘子为 $\lambda_1^* = 0, \lambda_2^* = 0, \lambda_3^* = 0$。

例2：带等式约束的问题

问题： $\begin{align} \min \quad & f(x_1, x_2) = x_1^2 + x_2^2 \\ \text{s.t.} \quad & h(x_1, x_2) = x_1 + x_2 - 1 = 0 \end{align}$

解：

步骤1：构造拉格朗日函数 $L(x_1, x_2, \nu) = x_1^2 + x_2^2 + \nu(x_1 + x_2 - 1)$

步骤2：写出KKT条件 $\begin{cases} \frac{\partial L}{\partial x_1} = 2x_1 + \nu = 0 \\ \frac{\partial L}{\partial x_2} = 2x_2 + \nu = 0 \\ x_1 + x_2 - 1 = 0 \end{cases}$

步骤3：求解从前两个方程得：$x_1 = x_2 = -\frac{\nu}{2}$ 代入第三个方程：$-\frac{\nu}{2} - \frac{\nu}{2} = 1$，得 $\nu = -1$ 因此：$x_1 = x_2 = \frac{1}{2}$

结论：最优解为 $x^* = (\frac{1}{2}, \frac{1}{2})$，对应的乘子为 $\nu^* = -1$。

例3：复杂的约束优化问题

问题： $\begin{align} \min \quad & f(x_1, x_2) = x_1^2 + 2x_2^2 - 4x_1 - 4x_2 \\ \text{s.t.} \quad & g_1(x_1, x_2) = x_1 + x_2 - 3 \leq 0 \\ & g_2(x_1, x_2) = -x_1 - 2x_2 + 5 \leq 0 \end{align}$

解：

步骤1：构造拉格朗日函数 $L(x_1, x_2, \lambda_1, \lambda_2) = x_1^2 + 2x_2^2 - 4x_1 - 4x_2 + \lambda_1(x_1 + x_2 - 3) + \lambda_2(-x_1 - 2x_2 + 5)$

步骤2：写出KKT条件 $\begin{cases} \frac{\partial L}{\partial x_1} = 2x_1 - 4 + \lambda_1 - \lambda_2 = 0 \\ \frac{\partial L}{\partial x_2} = 4x_2 - 4 + \lambda_1 - 2\lambda_2 = 0 \\ x_1 + x_2 - 3 \leq 0, \quad -x_1 - 2x_2 + 5 \leq 0 \\ \lambda_1 \geq 0, \quad \lambda_2 \geq 0 \\ \lambda_1(x_1 + x_2 - 3) = 0, \quad \lambda_2(-x_1 - 2x_2 + 5) = 0 \end{cases}$

步骤3：分情况讨论

情况1：$\lambda_1 = 0, \lambda_2 = 0$

从KKT条件得：$x_1 = 2, x_2 = 1$
检查约束：$g_1(2,1) = 0 \leq 0$，$g_2(2,1) = 1 > 0$
结论：不满足约束，舍去

情况2：$\lambda_1 = 0, \lambda_2 > 0$

从互补松弛性：$-x_1 - 2x_2 + 5 = 0$，即 $x_1 + 2x_2 = 5$
从KKT条件：$2x_1 - 4 - \lambda_2 = 0$，$4x_2 - 4 - 2\lambda_2 = 0$
解得：$x_1 = \frac{7}{3}, x_2 = \frac{4}{3}, \lambda_2 = \frac{2}{3}$
检查约束：$g_1(\frac{7}{3}, \frac{4}{3}) = \frac{2}{3} > 0$
结论：不满足约束，舍去

情况3：$\lambda_1 > 0, \lambda_2 = 0$

从互补松弛性：$x_1 + x_2 - 3 = 0$，即 $x_1 + x_2 = 3$
从KKT条件：$2x_1 - 4 + \lambda_1 = 0$，$4x_2 - 4 + \lambda_1 = 0$
解得：$x_1 = 2, x_2 = 1, \lambda_1 = 0$
结论：与假设 $\lambda_1 > 0$ 矛盾，舍去

情况4：$\lambda_1 > 0, \lambda_2 > 0$

从互补松弛性：$x_1 + x_2 = 3$ 且 $x_1 + 2x_2 = 5$
解得：$x_1 = 1, x_2 = 2$
从KKT条件：$\lambda_1 = 8, \lambda_2 = 6$
检查约束：$g_1(1,2) = 0 \leq 0$，$g_2(1,2) = 0 \leq 0$
结论：满足所有条件

步骤4：计算目标函数值 $f(1,2) = 1^2 + 2(2)^2 - 4(1) - 4(2) = 1 + 8 - 4 - 8 = -3$

结论：最优解为 x^* = (1, 2)，对应的乘子为 λ₁* = 8, λ₂* = 6，最优值为 f* = -3。

六、二阶最优性条件

6.1 二阶必要条件

设 $x^*$ 是约束优化问题的局部最优解，且满足KKT条件，则对于所有满足以下条件的 $d \neq 0$：

$\nabla g_i(x^*)^T d = 0$ 对所有 $i \in \mathcal{A}(x^*)$（起作用的不等式约束）
$\nabla h_j(x^*)^T d = 0$ 对所有 $j = 1, \ldots, q$（等式约束）

有： $d^T \nabla^2 L(x^*, \lambda^*, \nu^*) d \geq 0$

其中 $\nabla^2 L(x^*, \lambda^*, \nu^*)$ 是拉格朗日函数关于 $x$ 的Hessian矩阵。

6.2 二阶充分条件

设 $x^*$ 满足KKT条件，且对于所有满足上述条件的 $d \neq 0$，有： $d^T \nabla^2 L(x^*, \lambda^*, \nu^*) d > 0$

则 $x^*$ 是严格局部最优解。

6.3 正则点

定义：设 $x^$ 是约束优化问题的可行点，如果所有起作用约束的梯度线性无关，则称 $x^$ 为正则点。

重要性：正则点是KKT条件成立的重要前提条件。

6.4 二阶条件应用实例

问题：考虑优化问题 $\begin{align} \min \quad & f(x_1, x_2) = x_1 \\ \text{s.t.} \quad & g(x_1, x_2) = 3(x_1-3)^2 + x_2 \geq 0 \\ & h(x_1, x_2) = (x_1-3)^2 + x_2^2 - 10 = 0 \end{align}$

判断点 $x^{(1)} = (2, -3)^T$ 是否为局部最优解。

解：

步骤1：构造拉格朗日函数 $L(x_1, x_2, \lambda, \mu) = x_1 - \lambda[3(x_1-3)^2 + x_2] - \mu[(x_1-3)^2 + x_2^2 - 10]$

步骤2：计算梯度 $\nabla f(x) = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad \nabla g(x) = \begin{pmatrix} 6(x_1-3) \\ 1 \end{pmatrix}, \quad \nabla h(x) = \begin{pmatrix} 2(x_1-3) \\ 2x_2 \end{pmatrix}$

步骤3：在点 $x^{(1)} = (2, -3)^T$ 处计算梯度 $\nabla f(2, -3) = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad \nabla g(2, -3) = \begin{pmatrix} -6 \\ 1 \end{pmatrix}, \quad \nabla h(2, -3) = \begin{pmatrix} -2 \\ -6 \end{pmatrix}$

步骤4：检查KKT条件 $\nabla f(2, -3) - \lambda \nabla g(2, -3) - \mu \nabla h(2, -3) = \begin{pmatrix} 1 \\ 0 \end{pmatrix} - \lambda \begin{pmatrix} -6 \\ 1 \end{pmatrix} - \mu \begin{pmatrix} -2 \\ -6 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}$

得到方程组： $\begin{cases} 1 + 6\lambda + 2\mu = 0 \\ -\lambda + 6\mu = 0 \end{cases}$

解得：$\lambda = -\frac{3}{19} < 0$，$\mu = -\frac{1}{38}$

步骤5：判断KKT条件由于 $\lambda < 0$ 违反了KKT条件中的对偶可行性条件（$\lambda \geq 0$），因此 $x^{(1)} = (2, -3)^T$ 不满足KKT条件。

结论：$x^{(1)} = (2, -3)^T$ 不是局部最优解。

七、KKT条件的特殊情况

7.1 只有不等式约束

当 $q = 0$（无等式约束）时，KKT条件简化为： $\begin{cases} \nabla f(x^*) + \sum_{i=1}^p \lambda_i^* \nabla g_i(x^*) = 0 \\ g_i(x^*) \leq 0, \quad i = 1, \ldots, p \\ \lambda_i^* \geq 0, \quad i = 1, \ldots, p \\ \lambda_i^* g_i(x^*) = 0, \quad i = 1, \ldots, p \end{cases}$

7.2 只有等式约束

当 $p = 0$（无不等式约束）时，KKT条件简化为拉格朗日乘数法： $\begin{cases} \nabla f(x^*) + \sum_{j=1}^q \nu_j^* \nabla h_j(x^*) = 0 \\ h_j(x^*) = 0, \quad j = 1, \ldots, q \end{cases}$

7.3 凸优化问题

对于凸优化问题，KKT条件不仅是必要条件，也是充分条件。如果目标函数和约束函数都是凸函数，则满足KKT条件的点就是全局最优解。

八、KKT条件的计算步骤

8.1 一般计算流程

构造拉格朗日函数
写出KKT条件
分析约束的起作用情况
求解方程组
验证解的可行性

8.2 注意事项

约束条件：确保LICQ等约束条件得到满足
乘子符号：不等式约束的乘子必须非负
互补松弛性：不起作用的约束对应的乘子为零
唯一性：KKT条件提供的是必要条件，不是充分条件

九、KKT条件的实际应用

9.1 支持向量机

在支持向量机中，KKT条件用于：

确定支持向量
计算最优分离超平面
理解软间隔分类器

相关文章:

《最优化理论基础》

《最优化理论基础例题集》

《惩罚函数法》

《内点法》

约束优化问题的核心最优性条件