最优化理论——基础(凸集，凸函数，共轭函数等) - DoraemonJack的博客

最优化理论是现代数学和工程学的重要分支，其核心建立在凸分析和对偶理论的基础之上。本文将从最基础的凸集和凸函数概念出发，逐步深入到共轭函数、拉格朗日对偶等高级理论，为读者构建完整的最优化理论基础。

一、凸集理论

1.1 凸集的定义

定义1.1 设 $C \subseteq \mathbb{R}^n$，如果对于任意 $x_1, x_2 \in C$ 和任意 $\lambda \in [0,1]$，都有 $\lambda x_1 + (1-\lambda) x_2 \in C$ 则称 $C$ 为凸集。

几何意义：凸集中任意两点的连线都在该集合内。

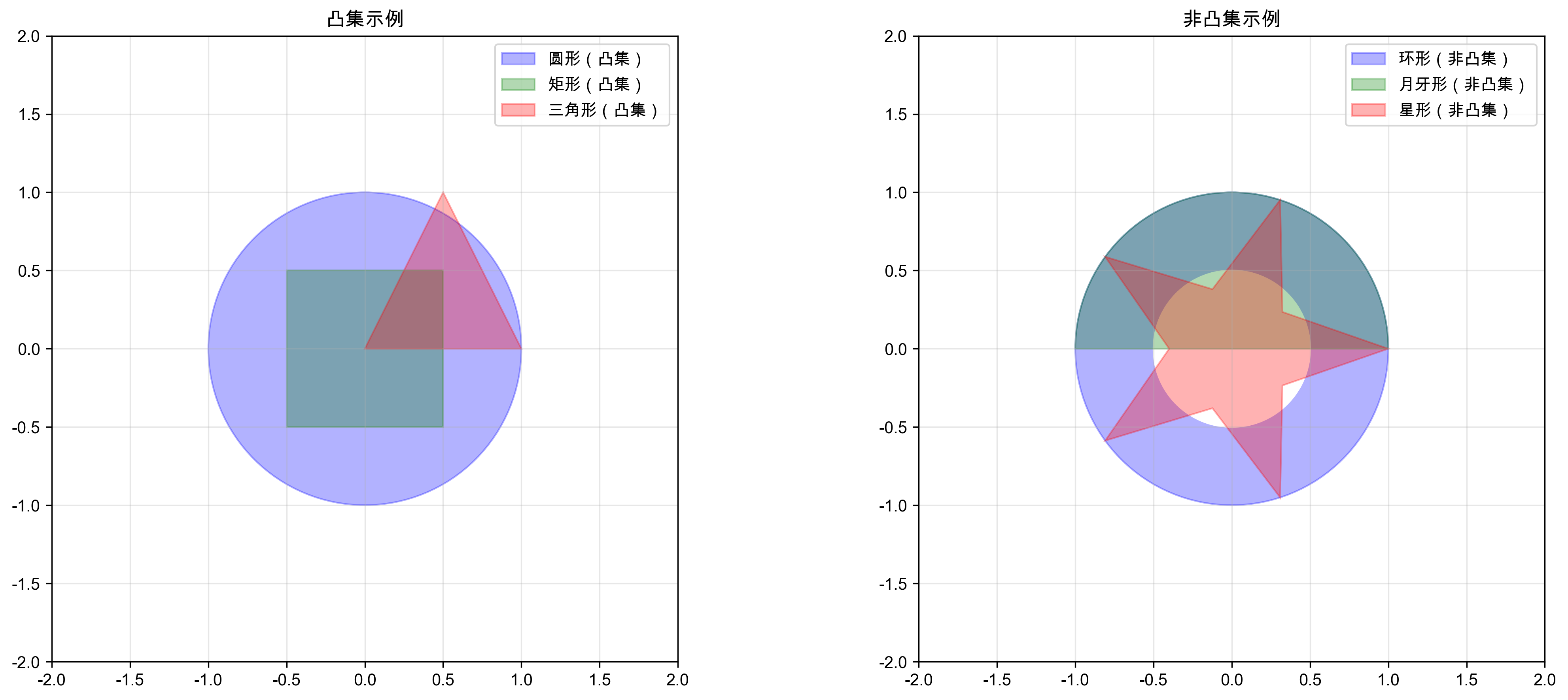
凸集与非凸集对比

1.2 凸集的基本性质

定理1.1 凸集的交集是凸集。证明：设 $\{C_i\}_{i \in I}$ 是一族凸集，$C = \bigcap_{i \in I} C_i$。对于任意 $x_1, x_2 \in C$ 和 $\lambda \in [0,1]$，由于 $x_1, x_2 \in C_i$ 对所有 $i$ 成立，且 $C_i$ 是凸集，所以 $\lambda x_1 + (1-\lambda) x_2 \in C_i$ 对所有 $i$ 成立，因此 $\lambda x_1 + (1-\lambda) x_2 \in C$。

定理1.2 凸集的仿射变换是凸集。证明：设 $C \subseteq \mathbb{R}^n$ 是凸集，$A: \mathbb{R}^n \to \mathbb{R}^m$ 是仿射变换，即 $A(x) = Ax + b$。对于任意 $y_1, y_2 \in A(C)$，存在 $x_1, x_2 \in C$ 使得 $y_1 = Ax_1 + b$，$y_2 = Ax_2 + b$。对于 $\lambda \in [0,1]$： $\lambda y_1 + (1-\lambda) y_2 = \lambda(Ax_1 + b) + (1-\lambda)(Ax_2 + b) = A(\lambda x_1 + (1-\lambda) x_2) + b$ 由于 $C$ 是凸集，$\lambda x_1 + (1-\lambda) x_2 \in C$，所以 $\lambda y_1 + (1-\lambda) y_2 \in A(C)$。

1.3 重要的凸集

超平面：$H = {x \in \mathbb{R}^n : a^T x = b}$，其中 $a \in \mathbb{R}^n \setminus \{0\}$，$b \in \mathbb{R}$。

半空间：$H^+ = {x \in \mathbb{R}^n : a^T x \geq b}$，$H^- = {x \in \mathbb{R}^n : a^T x \leq b}$。

多面体：有限个半空间的交集，即 ${x \in \mathbb{R}^n : Ax \leq b}$。

椭球：${x \in \mathbb{R}^n : (x-c)^T P^{-1} (x-c) \leq 1}$，其中 $P \succ 0$。

1.4 凸包

定义1.2 设 $S \subseteq \mathbb{R}^n$，$S$ 的凸包 $\text{conv}(S)$ 是包含 $S$ 的最小凸集，即 $\text{conv}(S) = \left\{\sum_{i=1}^k \lambda_i x_i : k \in \mathbb{N}, x_i \in S, \lambda_i \geq 0, \sum_{i=1}^k \lambda_i = 1\right\}$

Carathéodory定理：设 $S \subseteq \mathbb{R}^n$，则 $\text{conv}(S)$ 中的任意点都可以表示为 $S$ 中至多 $n+1$ 个点的凸组合。

1.5 凸集的分离定理

定理1.3（分离超平面定理） 设 $C$ 和 $D$ 是两个不相交的凸集，则存在超平面 $H = {x : a^T x = b}$ 使得 $C \subseteq H^+$ 且 $D \subseteq H^-$。

定理1.4（支撑超平面定理） 设 $C$ 是凸集，$x_0 \in \partial C$（边界），则存在超平面 $H = {x : a^T x = b}$ 使得 $C \subseteq H^+$ 且 $x_0 \in H$。

1.6 凸集例题

例1.1 证明以下集合是凸集：

$C_1 = {x \in \mathbb{R}^n : |x|_2 \leq 1}$（单位球）
$C_2 = {x \in \mathbb{R}^n : Ax = b}$（仿射集）
$C_3 = {x \in \mathbb{R}^n : x_i \geq 0, i = 1, \ldots, n}$（非负象限）

解：

对于 $x_1, x_2 \in C_1$ 和 $\lambda \in [0,1]$： $\|\lambda x_1 + (1-\lambda) x_2\|_2 \leq \lambda \|x_1\|_2 + (1-\lambda) \|x_2\|_2 \leq \lambda + (1-\lambda) = 1$ 因此 $\lambda x_1 + (1-\lambda) x_2 \in C_1$。
对于 $x_1, x_2 \in C_2$ 和 $\lambda \in [0,1]$： $A(\lambda x_1 + (1-\lambda) x_2) = \lambda Ax_1 + (1-\lambda) Ax_2 = \lambda b + (1-\lambda) b = b$ 因此 $\lambda x_1 + (1-\lambda) x_2 \in C_2$。
对于 $x_1, x_2 \in C_3$ 和 $\lambda \in [0,1]$： $(\lambda x_1 + (1-\lambda) x_2)_i = \lambda (x_1)_i + (1-\lambda) (x_2)_i \geq 0$ 因此 $\lambda x_1 + (1-\lambda) x_2 \in C_3$。

例1.2 设 $C = {x \in \mathbb{R}^2 : x_1^2 + x_2^2 \leq 1, x_1 \geq 0}$，求 $C$ 的凸包。

解：$C$ 本身就是凸集，因此 $\text{conv}(C) = C$。

例1.3 设 $S = {(0,0), (1,0), (0,1)}$，求 $\text{conv}(S)$。

解：$\text{conv}(S) = {\lambda_1(0,0) + \lambda_2(1,0) + \lambda_3(0,1) : \lambda_i \geq 0, \sum_{i=1}^3 \lambda_i = 1}$ $= \{(\lambda_2, \lambda_3) : \lambda_2, \lambda_3 \geq 0, \lambda_2 + \lambda_3 \leq 1\}$ 这是以 $(0,0), (1,0), (0,1)$ 为顶点的三角形。

二、凸函数理论

2.1 凸函数的定义

定义2.1 设 $f: C \to \mathbb{R}$，其中 $C \subseteq \mathbb{R}^n$ 是凸集。如果对于任意 $x_1, x_2 \in C$ 和任意 $\lambda \in [0,1]$，都有 $f(\lambda x_1 + (1-\lambda) x_2) \leq \lambda f(x_1) + (1-\lambda) f(x_2)$ 则称 $f$ 为凸函数。

定义2.2 如果上述不等式严格成立（当 $x_1 \neq x_2$ 且 $\lambda \in (0,1)$ 时），则称 $f$ 为严格凸函数。

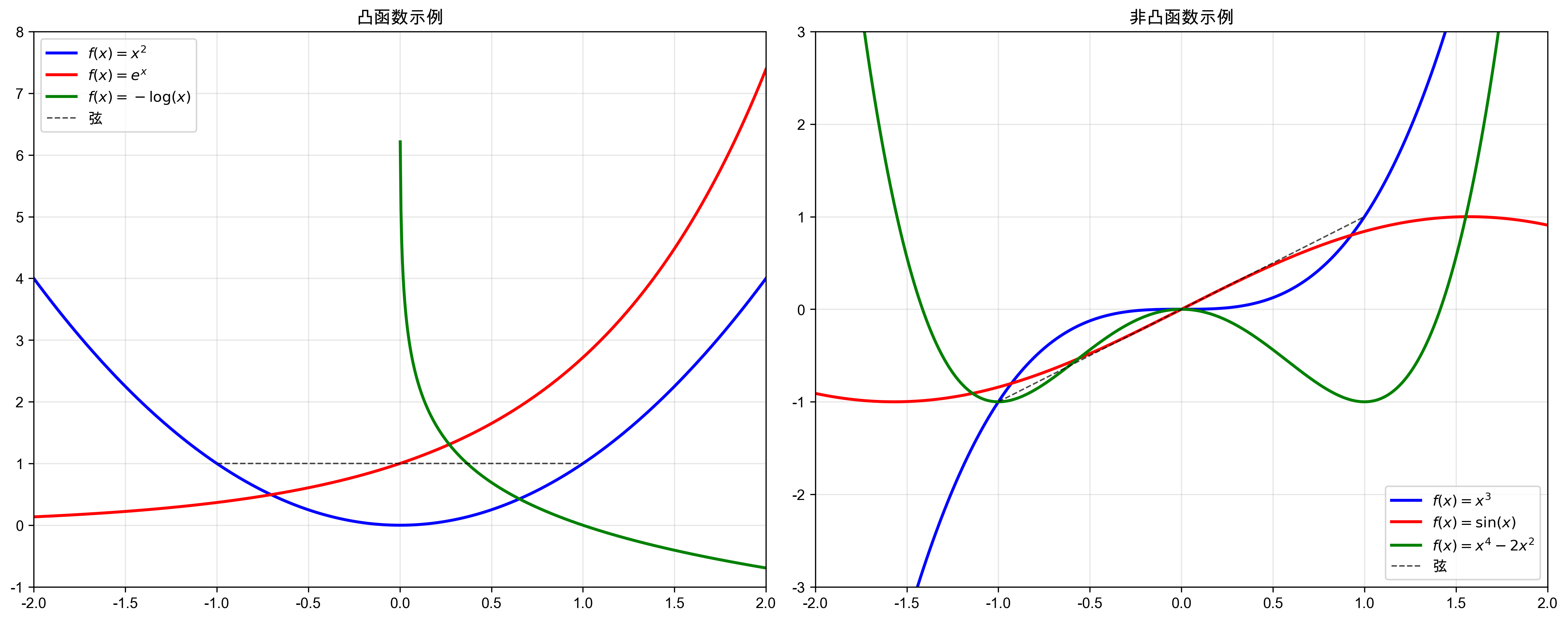
凸函数与非凸函数对比

2.2 凸函数的等价刻画

定理2.1 设 $f: C \to \mathbb{R}$ 在凸集 $C$ 上可微，则 $f$ 是凸函数当且仅当 $f(y) \geq f(x) + \nabla f(x)^T (y-x), \quad \forall x, y \in C$

定理2.2 设 $f: C \to \mathbb{R}$ 在凸集 $C$ 上二阶可微，则 $f$ 是凸函数当且仅当 $\nabla^2 f(x) \succeq 0, \quad \forall x \in C$ 即Hessian矩阵半正定。

2.3 凸函数的运算

定理2.3 设 $f_1, f_2$ 是凸函数，$\alpha, \beta \geq 0$，则 $\alpha f_1 + \beta f_2$ 是凸函数。

定理2.4 设 $f$ 是凸函数，$A$ 是仿射变换，则 $f \circ A$ 是凸函数。

定理2.5 设 $\{f_i\}_{i \in I}$ 是一族凸函数，则 $f(x) = \sup_{i \in I} f_i(x)$ 是凸函数。

2.4 重要的凸函数

二次函数：$f(x) = \frac{1}{2} x^T P x + q^T x + r$，其中 $P \succeq 0$。

范数函数：$f(x) = |x|_p$，其中 $p \geq 1$。

负对数函数：$f(x) = -\log x$，定义域为 $(0, \infty)$。

最大函数：$f(x) = \max{x_1, x_2, \ldots, x_n}$。

2.5 次梯度

定义2.3 设 $f: \mathbb{R}^n \to \mathbb{R}$ 是凸函数，$x \in \mathbb{R}^n$。如果 $g \in \mathbb{R}^n$ 满足 $f(y) \geq f(x) + g^T (y-x), \quad \forall y \in \mathbb{R}^n$ 则称 $g$ 为 $f$ 在 $x$ 处的次梯度。$f$ 在 $x$ 处的所有次梯度组成的集合称为次微分，记为 $\partial f(x)$。

性质：

如果 $f$ 在 $x$ 处可微，则 $\partial f(x) = {\nabla f(x)}$
$\partial f(x)$ 是闭凸集
如果 $f$ 在 $x$ 处连续，则 $\partial f(x)$ 非空有界

2.6 凸函数的运算

定理2.4 设 $f_1, f_2$ 是凸函数，$\alpha, \beta \geq 0$，则 $\alpha f_1 + \beta f_2$ 是凸函数。

定理2.5 设 $f$ 是凸函数，$A$ 是仿射变换，则 $f \circ A$ 是凸函数。

定理2.6 设 ${f_i}{i \in I}$ 是一族凸函数，则 $f(x) = \sup{i \in I} f_i(x)$ 是凸函数。

2.7 凸函数例题

例2.1 判断下列函数的凸性：

$f(x) = x^2$（$x \in \mathbb{R}$）
$f(x) = e^x$（$x \in \mathbb{R}$）
$f(x) = \log x$（$x > 0$）

解：

$f”(x) = 2 > 0$，因此 $f(x) = x^2$ 是凸函数。
$f”(x) = e^x > 0$，因此 $f(x) = e^x$ 是凸函数。
$f”(x) = -\frac{1}{x^2} < 0$，因此 $f(x) = \log x$ 是凹函数。

例2.2 设 $f(x) = \max{x_1, x_2, \ldots, x_n}$，证明 $f$ 是凸函数。

解：设 $x, y \in \mathbb{R}^n$，$\lambda \in [0,1]$，则 $f(\lambda x + (1-\lambda) y) = \max_i \{\lambda x_i + (1-\lambda) y_i\} \leq \lambda \max_i \{x_i\} + (1-\lambda) \max_i \{y_i\} = \lambda f(x) + (1-\lambda) f(y)$ 因此 $f$ 是凸函数。

例2.3 设 $f(x) = |x|_p$（$p \geq 1$），证明 $f$ 是凸函数。

例2.4 设 $f(x) = -\log x$（$x > 0$），求 $f$ 的次微分。

解：$f’(x) = -\frac{1}{x}$，因此 $\partial f(x) = {-\frac{1}{x}}$。

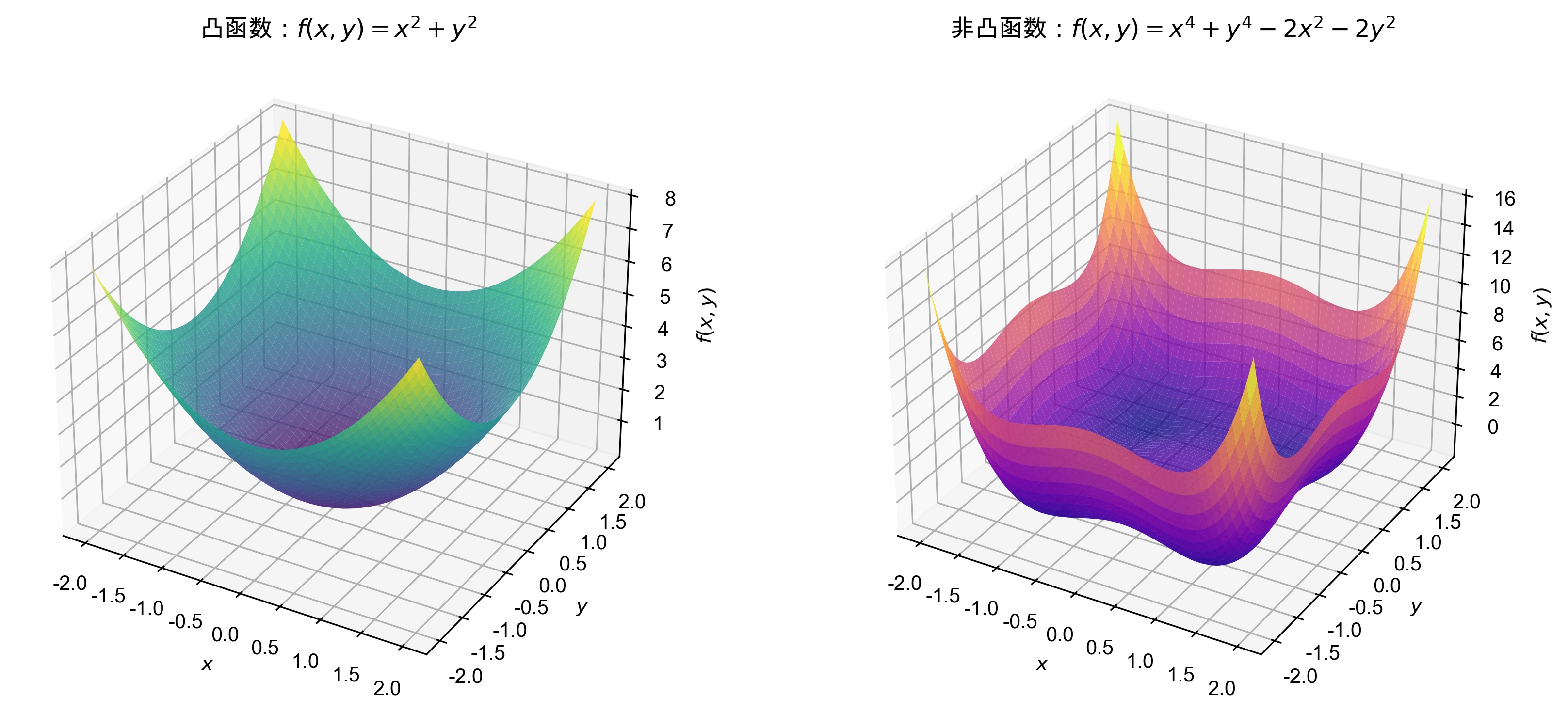
3D凸函数示例

三、共轭函数

3.1 共轭函数的定义

定义3.1 设 $f: \mathbb{R}^n \to \mathbb{R} \cup {+\infty}$，$f$ 的共轭函数定义为 $f^*(y) = \sup_{x \in \mathbb{R}^n} \{y^T x - f(x)\}$

几何意义：$f^*(y)$ 是 $f$ 的所有仿射下界 $y^T x - \alpha$ 中最大的 $\alpha$ 值。

🔍解释：一维问题的等价问题： $f^*(y) = - \inf_x \big( f(x) - yx \big)$ 假设：$l(x) = yx - c$ 看作一条斜率为 $y$ 的直线（在高维就是超平面），那么这条直线要想成为 $f(x)$ 的“支撑直线”，就必须满足： $l(x) \le f(x), \quad \forall x$ 也就是直线永远在函数曲线的下方。

共轭函数示例

3.2 共轭函数的基本性质

定理3.1 共轭函数 $f^*$ 是凸函数。

证明：设 $y_1, y_2 \in \mathbb{R}^n$，$\lambda \in [0,1]$，则 $\begin{align} f^*(\lambda y_1 + (1-\lambda) y_2) &= \sup_x \{(\lambda y_1 + (1-\lambda) y_2)^T x - f(x)\} \\ &= \sup_x \{\lambda(y_1^T x - f(x)) + (1-\lambda)(y_2^T x - f(x))\} \\ &\leq \lambda \sup_x \{y_1^T x - f(x)\} + (1-\lambda) \sup_x \{y_2^T x - f(x)\} \\ &= \lambda f^*(y_1) + (1-\lambda) f^*(y_2) \end{align}$

定理3.2 如果 $f$ 是闭凸函数，则 $f^{**} = f$。

3.3 重要函数的共轭

二次函数：设 $f(x) = \frac{1}{2} x^T P x$，其中 $P \succ 0$，则 $f^*(y) = \frac{1}{2} y^T P^{-1} y$

范数函数：设 $f(x) = |x|$，则 $f^*(y) = \begin{cases} 0, & \text{if } \|y\|_* \leq 1 \\ +\infty, & \text{otherwise} \end{cases}$ 其中 $|\cdot|_*$ 是对偶范数。

负对数函数：设 $f(x) = -\log x$，定义域为 $(0, \infty)$，则 $f^*(y) = \begin{cases} -1 - \log(-y), & \text{if } y < 0 \\ +\infty, & \text{otherwise} \end{cases}$

3.4 共轭函数的应用

Fenchel-Young不等式：对于任意 $x, y \in \mathbb{R}^n$， $f(x) + f^*(y) \geq x^T y$ 等号成立当且仅当 $y \in \partial f(x)$。

Fenchel对偶：考虑优化问题 $\min_{x} f(x) + g(Ax)$ 其对偶问题为 $\max_{y} -f^*(A^T y) - g^*(-y)$

四、最优性条件

4.1 无约束优化问题的最优性条件

考虑无约束优化问题： $\min_{x \in \mathbb{R}^n} f(x)$

一阶必要条件：设 $f$ 在 $x^*$ 处可微，如果 $x^*$ 是局部最优解，则 $\nabla f(x^*) = 0$

二阶必要条件：设 $f$ 在 $x^*$ 处二阶可微，如果 $x^*$ 是局部最优解，则 $\nabla f(x^*) = 0 \quad \text{且} \quad \nabla^2 f(x^*) \succeq 0$

二阶充分条件：设 $f$ 在 $x^*$ 处二阶可微，如果 $\nabla f(x^*) = 0 \quad \text{且} \quad \nabla^2 f(x^*) \succ 0$ 则 $x^*$ 是严格局部最优解。

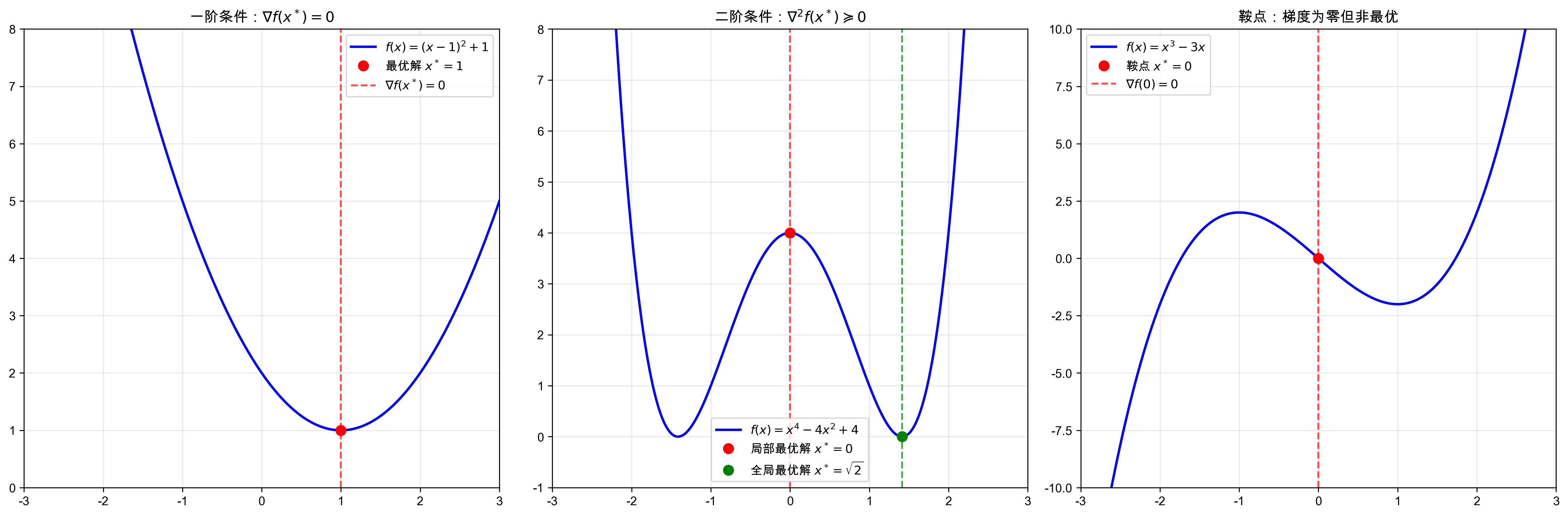
无约束优化问题最优性条件

证明一阶必要条件：设 $x^*$ 是局部最优解，则存在 $\delta > 0$ 使得 $f(x^*) \leq f(x)$ 对所有 $\|x - x^*\| < \delta$ 成立。

对于任意 $d \in \mathbb{R}^n$，考虑 $x = x^* + td$，其中 $t > 0$ 充分小使得 $|x - x^*| = t|d| < \delta$。

由泰勒展开： $f(x^* + td) = f(x^*) + t\nabla f(x^*)^T d + o(t)$

由于 $x^*$ 是局部最优解： $0 \leq f(x^* + td) - f(x^*) = t\nabla f(x^*)^T d + o(t)$

两边除以 $t$ 并令 $t \to 0$： $\nabla f(x^*)^T d \geq 0$

由于 $d$ 是任意的，取 $d = -\nabla f(x^*)$ 得到： $\nabla f(x^*)^T (-\nabla f(x^*)) = -\|\nabla f(x^*)\|^2 \geq 0$

因此 $\nabla f(x^*) = 0$。

4.2 约束优化问题的最优性条件

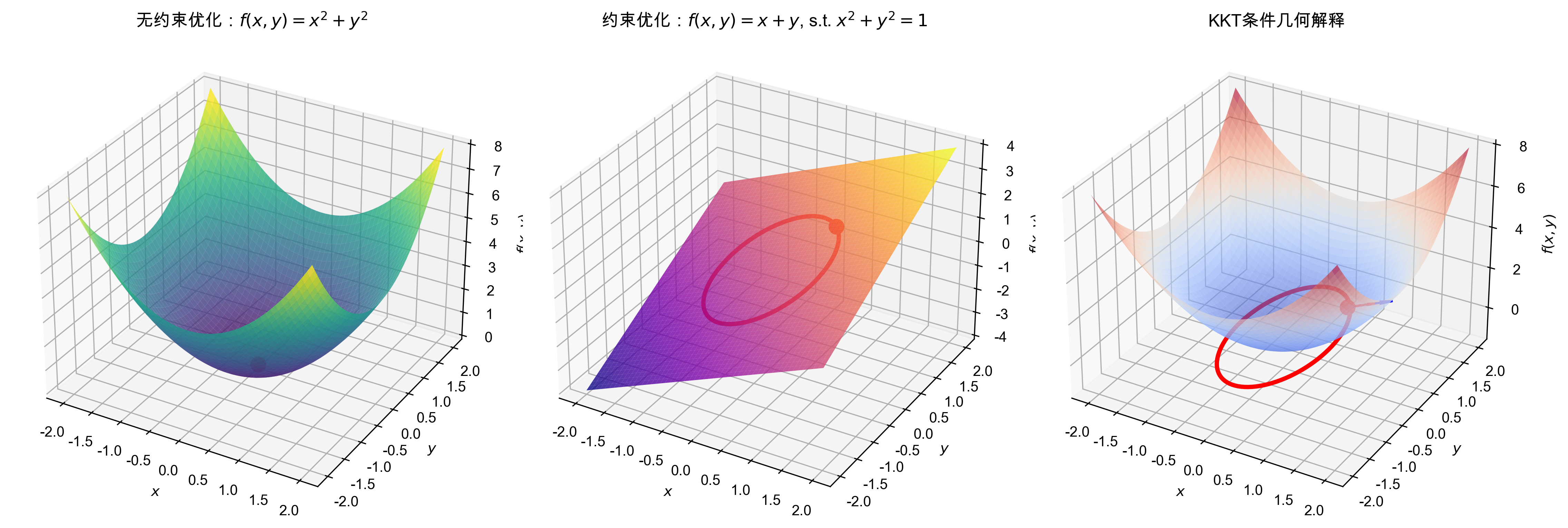
考虑约束优化问题： $\begin{align} \min \quad & f(x) \\ \text{s.t.} \quad & g_i(x) \leq 0, \quad i = 1, \ldots, m \\ & h_j(x) = 0, \quad j = 1, \ldots, p \end{align}$

拉格朗日函数： $L(x, \lambda, \nu) = f(x) + \sum_{i=1}^m \lambda_i g_i(x) + \sum_{j=1}^p \nu_j h_j(x)$

一阶必要条件（KKT条件）：设 $x^*$ 是局部最优解，且满足线性无关约束条件（LICQ），则存在拉格朗日乘子 $\lambda^* \geq 0$ 和 $\nu^*$ 使得：

平稳性条件：$\nabla_x L(x^*, \lambda^*, \nu^*) = 0$
原始可行性：$g_i(x^*) \leq 0$，$h_j(x^*) = 0$
对偶可行性：$\lambda_i^* \geq 0$
互补松弛性：$\lambda_i^* g_i(x^*) = 0$

二阶充分条件：设 $x^*$ 满足KKT条件，且对于所有满足以下条件的 $d \neq 0$：

$\nabla g_i(x^*)^T d = 0$ 对所有 $\in \mathcal{A}(x^*)$（起作用的不等式约束）
$\nabla h_j(x^*)^T d = 0$ 对所有 $j$

都有 $d^T \nabla_{xx}^2 L(x^*, \lambda^*, \nu^*) d > 0$

则 $x^*$ 是严格局部最优解。

4.3 线性无关约束条件（LICQ）

定义4.1 在点 $x$ 处，如果起作用约束的梯度向量线性无关，即 $\{\nabla g_i(x) : i \in \mathcal{A}(x)\} \cup \{\nabla h_j(x) : j = 1, \ldots, p\}$ 线性无关，则称满足线性无关约束条件（LICQ）。

其中 $\mathcal{A}(x) = {i : g_i(x) = 0}$ 是起作用的不等式约束集合。

4.4 约束优化问题的几何解释

切锥和法锥：

切锥：$T(x) = {d : \nabla g_i(x)^T d \leq 0, \forall i \in \mathcal{A}(x), \nabla h_j(x)^T d = 0, \forall j}$
法锥：$N(x) = {\sum_{i \in \mathcal{A}(x)} \lambda_i \nabla g_i(x) + \sum_j \nu_j \nabla h_j(x) : \lambda_i \geq 0}$

几何最优性条件：在最优解 $x^$ 处，目标函数的负梯度 $-f(x^)$ 必须属于法锥 $N(x^*)$，即 $-\nabla f(x^*) \in N(x^*)$

这等价于存在 $\lambda^* \geq 0$ 和 $\nu^*$ 使得 $\nabla f(x^*) + \sum_{i \in \mathcal{A}(x^*)} \lambda_i^* \nabla g_i(x^*) + \sum_j \nu_j^* \nabla h_j(x^*) = 0$

约束优化问题最优性条件

4.5 特殊情况的KKT条件

只有等式约束： $\begin{align} \min \quad & f(x) \\ \text{s.t.} \quad & h_j(x) = 0, \quad j = 1, \ldots, p \end{align}$

KKT条件简化为：

\[\nabla f(x^*) + \sum_{j=1}^p \nu_j^* \nabla h_j(x^*) = 0\]
\[h_j(x^*) = 0, \quad j = 1, \ldots, p\]

只有不等式约束： $\begin{align} \min \quad & f(x) \\ \text{s.t.} \quad & g_i(x) \leq 0, \quad i = 1, \ldots, m \end{align}$

KKT条件为：

$\nabla f(x^) + \sum_{i=1}^m \lambda_i^ \nabla g_i(x^*) = 0$
$g_i(x^*) \leq 0, \quad i = 1, \ldots, m$
$\lambda_i^* \geq 0, \quad i = 1, \ldots, m$
$\lambda_i^* g_i(x^*) = 0, \quad i = 1, \ldots, m$

4.6 最优性条件的应用

例4.1 考虑问题 $\begin{align} \min \quad & x_1^2 + x_2^2 \\ \text{s.t.} \quad & x_1 + x_2 \geq 1 \\ & x_1 \geq 0, \quad x_2 \geq 0 \end{align}$

写出 KKT 条件并求所有候选点；
判断候选点是否满足二阶必要条件（写出临界锥并验证拉格朗日 Hessian 在其上半正定）。

解：拉格朗日函数：$L(x, \lambda) = x_1^2 + x_2^2 + \lambda_1(1 - x_1 - x_2) - \lambda_2 x_1 - \lambda_3 x_2$

KKT条件：

$\frac{\partial L}{\partial x_1} = 2x_1 - \lambda_1 - \lambda_2 = 0$
$\frac{\partial L}{\partial x_2} = 2x_2 - \lambda_1 - \lambda_3 = 0$
$x_1 + x_2 \geq 1, \quad x_1 \geq 0, \quad x_2 \geq 0$
$\lambda_1, \lambda_2, \lambda_3 \geq 0$
$\lambda_1(1 - x_1 - x_2) = 0, \quad \lambda_2 x_1 = 0, \quad \lambda_3 x_2 = 0$

分析：

如果 $x_1 > 0, x_2 > 0$，则 $\lambda_2 = \lambda_3 = 0$
如果 $x_1 + x_2 > 1$，则 $\lambda_1 = 0$，得到 $x_1 = x_2 = 0$，矛盾
因此 $x_1 + x_2 = 1$，且 $x_1 = x_2 = \frac{1}{2}$

验证：$x_1^* = x_2^* = \frac{1}{2}$ 满足所有KKT条件，是最优解。

二阶必要条件检验（主干流程）

拉格朗日 Hessian（对 $x$ 的二阶导）：

\[\nabla^2_{xx}\mathcal L = \nabla^2 f = \begin{pmatrix}2 & 0\\[4pt]0 & 2\end{pmatrix} = 2I.\]

（这里约束是线性的，故它们对 Hessian 没有二阶贡献。）

活跃约束集合 $\mathcal A$ 在 $x^\star$：

等式 $h$ 总是活动的 → $h$ 在 $\mathcal A$。
不等式 $g$ 在 $x^\star=(1/2,1/2)$ 是否活动？ $g(x^\star)=-x_1=-1/2<0$，所以 不活动（无等号）。且对应的 $\mu^\star=0$。

因此在该点只有等式约束在活跃集合里。

⭐临界锥（或切空间）$C$：
对于等式约束 $h$ 的切空间条件是 $\nabla h(x^\star)^\top d =0$。

⭐这里 $\nabla h=(1,1)$，所以$C = \{d=(d_1,d_2)\mid d_1+d_2=0\}.$（因为不等式不活动，所以没有额外的不等式约束限制。）
在临界方向 $d\in C$ 上检验二阶形式：
取任意 $d=(t,-t)$（$t\in\mathbb R$），

\[d^\top \nabla^2_{xx}\mathcal L\, d = (t,-t)\begin{pmatrix}2&0\\0&2\end{pmatrix}\begin{pmatrix}t\\-t\end{pmatrix} =2(t^2+t^2)=4t^2 \ge 0.\]

对所有临界方向均 $\ge0$，因此二阶必要条件成立。

进一步注意：当 $t\ne0$ 时上式严格 $>0$，所以实际上在临界锥上拉格朗日 Hessian 是正定的，从而满足二阶充分条件 → 说明这是严格局部最小点（受约束的局部极小）。

4.7 最优性条件例题

例4.2 考虑无约束优化问题：$\min f(x) = x^4 - 4x^2 + 4$

解：

一阶条件：$f’(x) = 4x^3 - 8x = 4x(x^2 - 2) = 0$ 解得：$x = 0$ 或 $x = \pm\sqrt{2}$
二阶条件：$f’‘(x) = 12x^2 - 8$
- $f’‘(0) = -8 < 0$，因此 $x = 0$ 是局部最大值
- $f’’(\pm\sqrt{2}) = 12 \cdot 2 - 8 = 16 > 0$，因此 $x = \pm\sqrt{2}$ 是局部最小值
全局最小值：$f(\pm\sqrt{2}) = 2 - 8 + 4 = -2$

例4.3 考虑约束优化问题： $\begin{align} \min \quad & f(x,y) = x^2 + y^2 \\ \text{s.t.} \quad & x + y = 1 \end{align}$

解：

拉格朗日函数：$L(x,y,\lambda) = x^2 + y^2 + \lambda(1 - x - y)$
KKT条件：
- $\frac{\partial L}{\partial x} = 2x - \lambda = 0$
- $\frac{\partial L}{\partial y} = 2y - \lambda = 0$
- $x + y = 1$
求解：从前两个方程得 $x = y = \frac{\lambda}{2}$，代入第三个方程： $\frac{\lambda}{2} + \frac{\lambda}{2} = 1$，得 $\lambda = 1$ 因此 $x^* = y^* = \frac{1}{2}$
验证：$f(\frac{1}{2}, \frac{1}{2}) = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}$

例4.4 考虑约束优化问题： $\begin{align} \min \quad & f(x,y) = x + y \\ \text{s.t.} \quad & x^2 + y^2 \leq 1 \\ & x \geq 0, \quad y \geq 0 \end{align}$

解：

拉格朗日函数：$L(x,y,\lambda_1,\lambda_2,\lambda_3) = x + y + \lambda_1(x^2 + y^2 - 1) - \lambda_2 x - \lambda_3 y$
KKT条件：
- $\frac{\partial L}{\partial x} = 1 + 2\lambda_1 x - \lambda_2 = 0$
- $\frac{\partial L}{\partial y} = 1 + 2\lambda_1 y - \lambda_3 = 0$
- $x^2 + y^2 \leq 1$，$x \geq 0$，$y \geq 0$
- $\lambda_1 \geq 0$，$\lambda_2 \geq 0$，$\lambda_3 \geq 0$
- $\lambda_1(x^2 + y^2 - 1) = 0$，$\lambda_2 x = 0$，$\lambda_3 y = 0$
分析：
- 如果 $x > 0, y > 0$，则 $\lambda_2 = \lambda_3 = 0$
- 如果 $x^2 + y^2 < 1$，则 $\lambda_1 = 0$，得到 $1 = 0$，矛盾
- 因此 $x^2 + y^2 = 1$，且 $x = y = \frac{1}{\sqrt{2}}$
验证：$f(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) = \frac{2}{\sqrt{2}} = \sqrt{2}$

3D最优性条件

五、应用实例

5.1 支持向量机

支持向量机可以表述为凸优化问题： $\begin{align} \min_{w,b,\xi} \quad & \frac{1}{2} \|w\|^2 + C \sum_{i=1}^n \xi_i \\ \text{s.t.} \quad & y_i(w^T x_i + b) \geq 1 - \xi_i \\ & \xi_i \geq 0 \end{align}$

其拉格朗日对偶为： $\begin{align} \max_{\alpha} \quad & \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j=1}^n \alpha_i \alpha_j y_i y_j x_i^T x_j \\ \text{s.t.} \quad & 0 \leq \alpha_i \leq C \\ & \sum_{i=1}^n \alpha_i y_i = 0 \end{align}$

5.2 最小二乘问题

考虑带约束的最小二乘问题： $\begin{align} \min \quad & \|Ax - b\|^2 \\ \text{s.t.} \quad & Cx = d \end{align}$

其拉格朗日函数为： $L(x, \nu) = \|Ax - b\|^2 + \nu^T(Cx - d)$

KKT条件给出： $2A^T(Ax^* - b) + C^T \nu^* = 0, \quad Cx^* = d$

5.3 投资组合优化

Markowitz投资组合优化问题： $\begin{align} \min \quad & x^T \Sigma x \\ \text{s.t.} \quad & \mu^T x \geq r \\ & 1^T x = 1 \\ & x \geq 0 \end{align}$

其中 $\Sigma$ 是协方差矩阵，$\mu$ 是期望收益向量，$r$ 是目标收益。

六、强对偶与弱对偶的通俗解释

6.1 生活中的对偶关系

想象一个买卖交易的场景：

原问题（卖家视角）：

目标：最小化成本，以最低价格出售商品
约束：必须满足买家的基本要求

对偶问题（买家视角）：

目标：最大化效用，获得最大的满足感
约束：预算有限，不能超过可承受的价格

6.2 弱对偶：永远存在的差距

弱对偶定理：卖家的最低成本 ≥ 买家的最大效用

通俗理解：

卖家再便宜，也不可能低于买家的心理预期
买家再满意，也不可能超过卖家的成本底线
这个差距就是对偶间隙

数学表达： $f(x^*) \geq g(\lambda^*, \mu^*)$

其中：

$f(x^*)$：原问题的最优值（卖家成本）
$g(\lambda^*, \mu^*)$：对偶问题的最优值（买家效用）

6.3 强对偶：完美的平衡

强对偶：当对偶间隙为0时，即 $f(x^*) = g(\lambda^*, \mu^*)$

通俗理解：

卖家的最低成本 = 买家的最大效用
市场达到完美均衡，没有浪费
这是经济学中的帕累托最优状态

现实意义：

在完全竞争市场中，价格等于边际成本
资源得到最优配置，没有效率损失

6.4 对偶间隙的直观理解

对偶间隙 = 原问题最优值 - 对偶问题最优值

情况	对偶间隙	含义	现实例子
强对偶	Gap = 0	完美均衡	完全竞争市场
弱对偶	Gap > 0	存在效率损失	垄断市场、信息不对称

6.5 为什么需要理解对偶？

1. 算法设计：

对偶问题通常更容易求解
提供原问题解的下界估计
用于设计高效的优化算法

6.6 弱对偶定理的证明

定理：设 $x$ 是原问题的可行解，$(\lambda, \mu)$ 是对偶问题的可行解，则 $f(x) \geq g(\lambda, \mu)$

证明：

步骤1：构造拉格朗日函数 $L(x, \lambda, \mu) = f(x) - \sum_{i=1}^m \lambda_i g_i(x) - \sum_{j=1}^l \mu_j h_j(x)$

步骤2：分析可行性条件

由于 $x$ 是原问题的可行解：

$g_i(x) \geq 0, \quad i = 1, \ldots, m$
$h_j(x) = 0, \quad j = 1, \ldots, l$

由于 $(\lambda, \mu)$ 是对偶问题的可行解：

$\lambda_i \geq 0, \quad i = 1, \ldots, m$

步骤3：推导不等式

因为 $\lambda_i \geq 0$ 且 $g_i(x) \geq 0$，所以： $\sum_{i=1}^m \lambda_i g_i(x) \geq 0$

因为 $h_j(x) = 0$，所以： $\sum_{j=1}^l \mu_j h_j(x) = 0$

步骤4：建立关系

因此： $L(x, \lambda, \mu) = f(x) - \sum_{i=1}^m \lambda_i g_i(x) - \sum_{j=1}^l \mu_j h_j(x) \leq f(x)$

步骤5：利用对偶函数定义

由于 $g(\lambda, \mu) = \inf_{x \in D} L(x, \lambda, \mu)$，而 $x \in D$，所以： $g(\lambda, \mu) \leq L(x, \lambda, \mu) \leq f(x)$

结论：$f(x) \geq g(\lambda, \mu)$

证毕。

6.7 强对偶定理的证明

定理：在凸优化问题中，如果Slater条件成立，则强对偶成立，即 $f(x^*) = g(\lambda^*, \mu^*)$

证明思路：设 $x^*$ 是原问题的最优解，$(\lambda^*, \mu^*)$ 是对偶问题的最优解。

由于满足KKT条件： $\nabla f(x^*) + \sum_{i=1}^m \lambda_i^* \nabla g_i(x^*) + \sum_{j=1}^l \mu_j^* \nabla h_j(x^*) = 0$

且： $\lambda_i^* g_i(x^*) = 0, \quad i = 1, \ldots, m$

因此： $L(x^*, \lambda^*, \mu^*) = f(x^*) - \sum_{i=1}^m \lambda_i^* g_i(x^*) - \sum_{j=1}^l \mu_j^* h_j(x^*) = f(x^*)$

由于 $g(\lambda^*, \mu^*) = \inf_{x \in D} L(x, \lambda^*, \mu^*)$，而 $x^* \in D$，所以： $g(\lambda^*, \mu^*) \leq L(x^*, \lambda^*, \mu^*) = f(x^*)$

由弱对偶定理：$f(x^*) \geq g(\lambda^*, \mu^*)$

因此：$f(x^*) = g(\lambda^*, \mu^*)$

证毕。

6.8 强对偶成立的条件

Slater条件：存在一个严格可行点

数学表述：$\exists \hat{x} \in \text{int}(D)$ 使得 $g_i(\hat{x}) > 0, h_j(\hat{x}) = 0$
通俗理解：问题不是”太紧”的约束

KKT条件：在最优解处满足

数学表述：平稳性、原始可行性、对偶可行性、互补松弛性
通俗理解：梯度平衡，没有”浪费”的约束

凸性条件：目标函数和约束都是凸的

数学表述：$f$ 和 $g_i$ 是凸函数，$h_j$ 是仿射函数
通俗理解：问题具有良好的几何性质

6.9 强对偶的几何解释

下图展示了强对偶的几何意义，其中原问题和对偶问题的最优值相等：

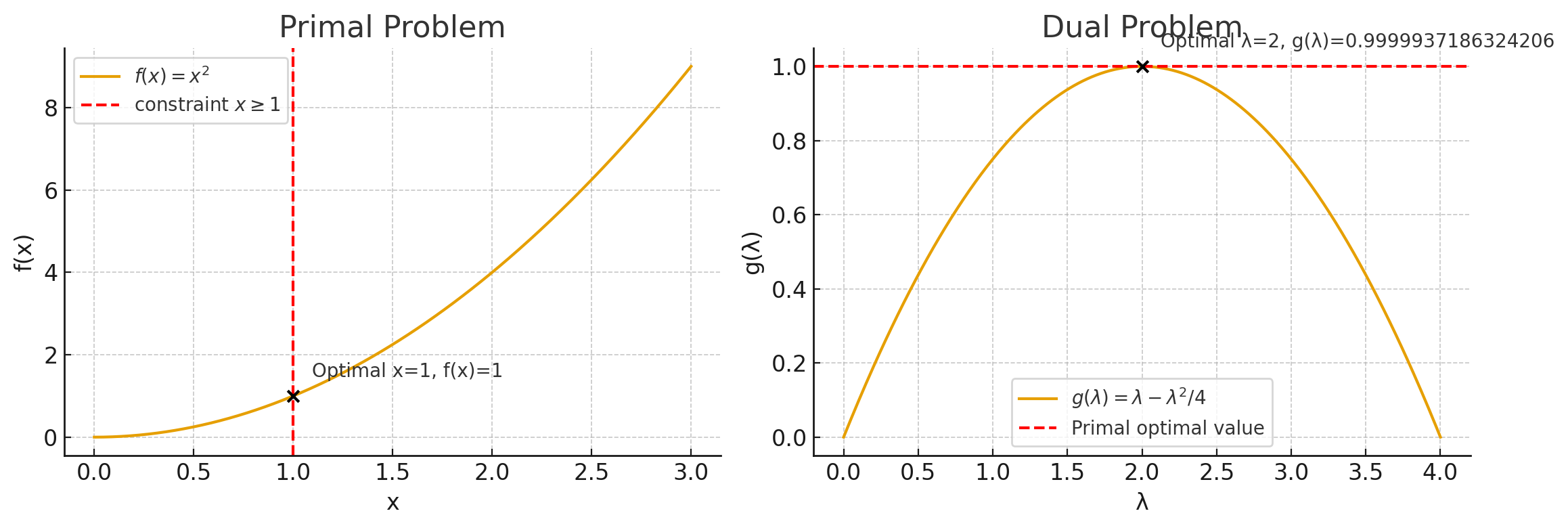
对偶问题几何解释

图中说明：

左侧图表（原问题）：

橙色曲线：目标函数 $f(x) = x^2$
红色虚线：约束条件 $x \geq 1$（垂直线）
黑色×标记：原问题的最优解 $x^* = 1$，最优值 $f(x^*) = 1$

右侧图表（对偶问题）：

橙色曲线：对偶函数 $g(\lambda) = \lambda - \frac{\lambda^2}{4}$
红色虚线：原问题的最优值参考线 $g(\lambda) = 1$
黑色×标记：对偶问题的最优解 $\lambda^* = 2$，最优值 $g(\lambda^*) \approx 1$

强对偶的几何意义：

原问题的最优值 = 对偶问题的最优值 = $1$
对偶间隙为0，表示没有效率损失
两个问题在几何上达到完美平衡

七、总结

最优化理论基础建立在以下几个核心概念之上：

凸集和凸函数：为优化问题提供了良好的几何和函数性质
证明一阶必要条件共轭函数：建立了函数与其对偶表示之间的联系
最优性条件：包括无约束和约束优化问题的完整最优性理论
对偶理论：通过强对偶和弱对偶理解优化问题的本质特征