惩罚函数法又称乘子法,是将约束优化问题转换为无约束优化问题的方法之一。其基本思想就是通过在原始的目标函数中添加一个障碍函数(也可以理解成惩罚函数)来代替约束条件中的不等式约束。如果当前解不满足约束条件,就在目标项上加上一个正向的惩罚(这里考虑的都是最小化问题),强迫当前解往可行域的方向走。至于正向惩罚的力度,取决于所用的映射函数,即惩罚函数。
一、非线性规划模型
\[\begin{cases} \min & f(\boldsymbol{x}) \\ \text{s.t.} & g_i(\boldsymbol{x}) \le 0,\quad i=1,\dots,p \\ & h_j(\boldsymbol{x}) = 0,\quad j=1,\dots,q \end{cases}\]其中,$f(\boldsymbol{x})$、$g_i(\boldsymbol{x})(i=1,2,\dots,p)$ 和 $h_j(\boldsymbol{x})(j=1,2,\dots,q)$ 是$\mathbb{R}^n$ 上的连续函数。
注意:后面惩罚函数的选取与这个模型相关,如果不等式约束方向相反惩罚函数就有所不同,也可以理解为该模型就是标准型。
由于约束条件是非线性的,不能用消元法将其转换为无约束问题,在求解时需同时考虑目标函数值下降和满足约束条件。可以通过由目标函数和约束条件组成惩罚函数,将原问题转化为极小化惩罚函数的无约束问题。
二、惩罚函数外点法
惩罚函数基本思想:通过构造惩罚函数将约束问题转化为无约束问题,进而用无约束最优化方法求解。主要分为内点法和外点法。注意:惩罚函数对目标函数的凹凸性没有要求,且结合启发式算法(如遗传算法、蚁群算法、禁忌搜索等)几乎可以求解任何问题,因为启发式算法无需目标函数的梯度等信息。外点法不保证搜索点保持在可行域内(搜索范围包括可行域和不可行域),适用于包含不等式约束或等式约束的优化问题。
外点法可视化说明
graph TD
A["初始点 x0"] --> B{"是否在可行域内?"}
B -->|是| C["惩罚项 = 0<br/>φ(x) = f(x)"]
B -->|否| D["惩罚项 > 0<br/>φ(x) = f(x) + r·[max(0,g(x))]²"]
C --> E["求解无约束优化<br/>min φ(x)"]
D --> E
E --> F["得到新点 x(k+1)"]
F --> G{"收敛?"}
G -->|否| H["增大惩罚参数 r<br/>r(k+1) = C·r(k)"]
H --> I["更新迭代点"]
I --> B
G -->|是| J["得到最优解 x*"]
style A fill:#e1f5fe
style J fill:#c8e6c9
style D fill:#ffcdd2
style C fill:#dcedc8
外点法特点:
- 🔵 蓝色区域:可行域(约束满足)
- 🔴 红色区域:不可行域(约束违反)
- 📍 搜索路径:可以从任意点开始,包括不可行域
- ⚡ 惩罚机制:在不可行域时施加惩罚,推动点向可行域移动
几何直观理解
graph LR
subgraph "搜索空间"
A["不可行域<br/>g(x) > 0<br/>惩罚项 > 0"]
B["可行域边界<br/>g(x) = 0"]
C["可行域<br/>g(x) ≤ 0<br/>惩罚项 = 0"]
end
D["初始点<br/>可在任意位置"] --> E["计算惩罚函数<br/>φ(x) = f(x) + r·[max(0,g(x))]²"]
E --> F["无约束优化<br/>min φ(x)"]
F --> G["新迭代点<br/>可能仍在不可行域"]
G --> H{"收敛?"}
H -->|否| I["增大r<br/>加强惩罚"]
I --> E
H -->|是| J["最优解<br/>通常在边界上"]
style A fill:#ffcdd2
style B fill:#fff3e0
style C fill:#dcedc8
style D fill:#e1f5fe
style J fill:#c8e6c9
关键理解:
- 外点法允许搜索点在可行域外部开始和移动
- 通过惩罚项将不可行域的点”推”向可行域
- 随着惩罚参数r增大,搜索点逐渐逼近可行域边界
- 最终收敛到约束边界上的最优解
惩罚函数法可视化
下图展示了惩罚函数法的基本概念和收敛过程:
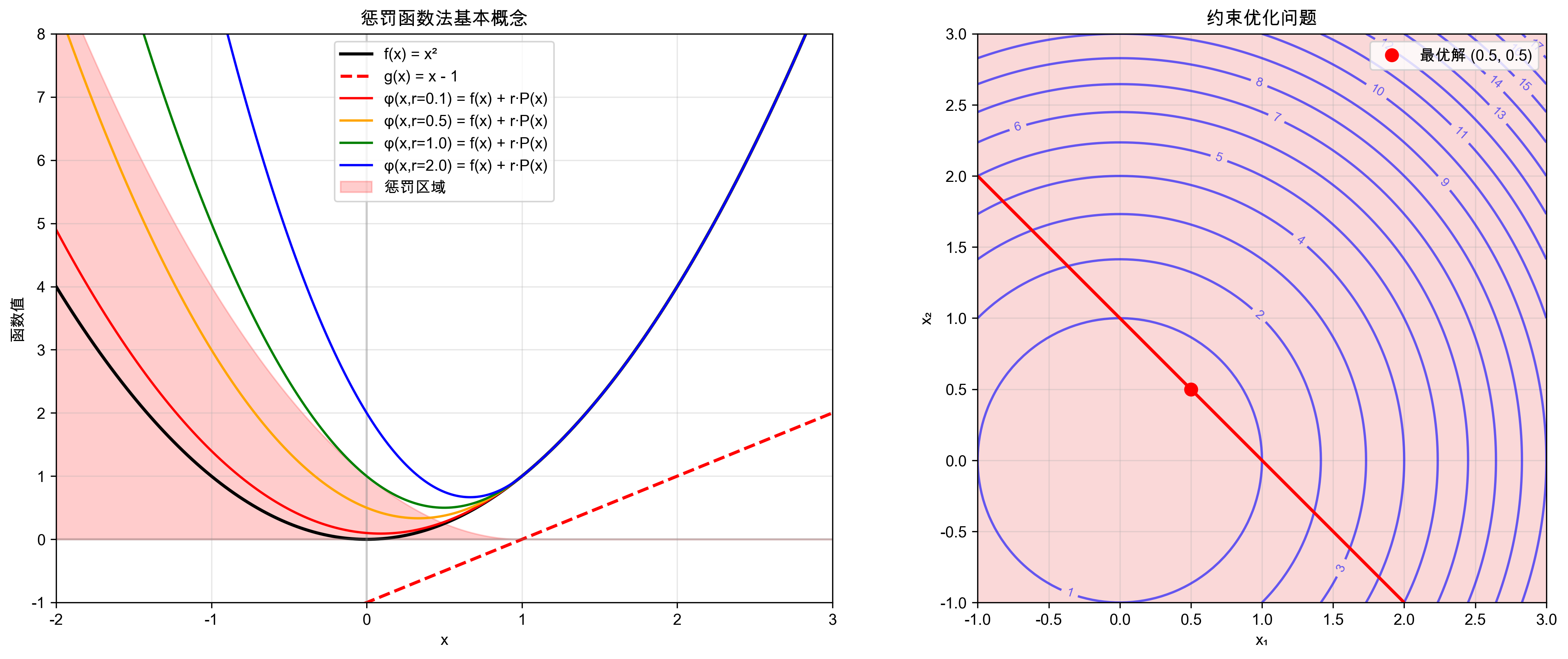
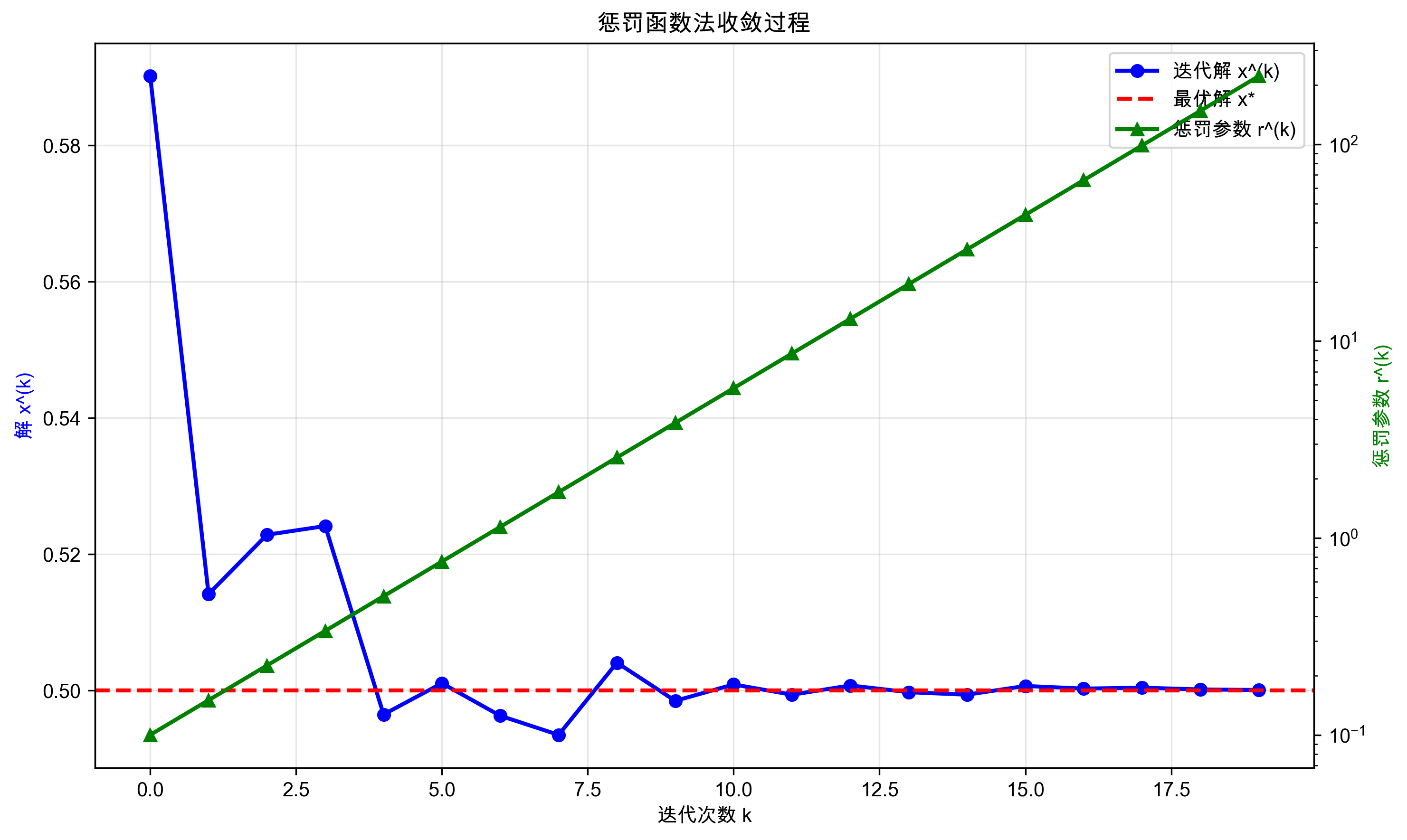
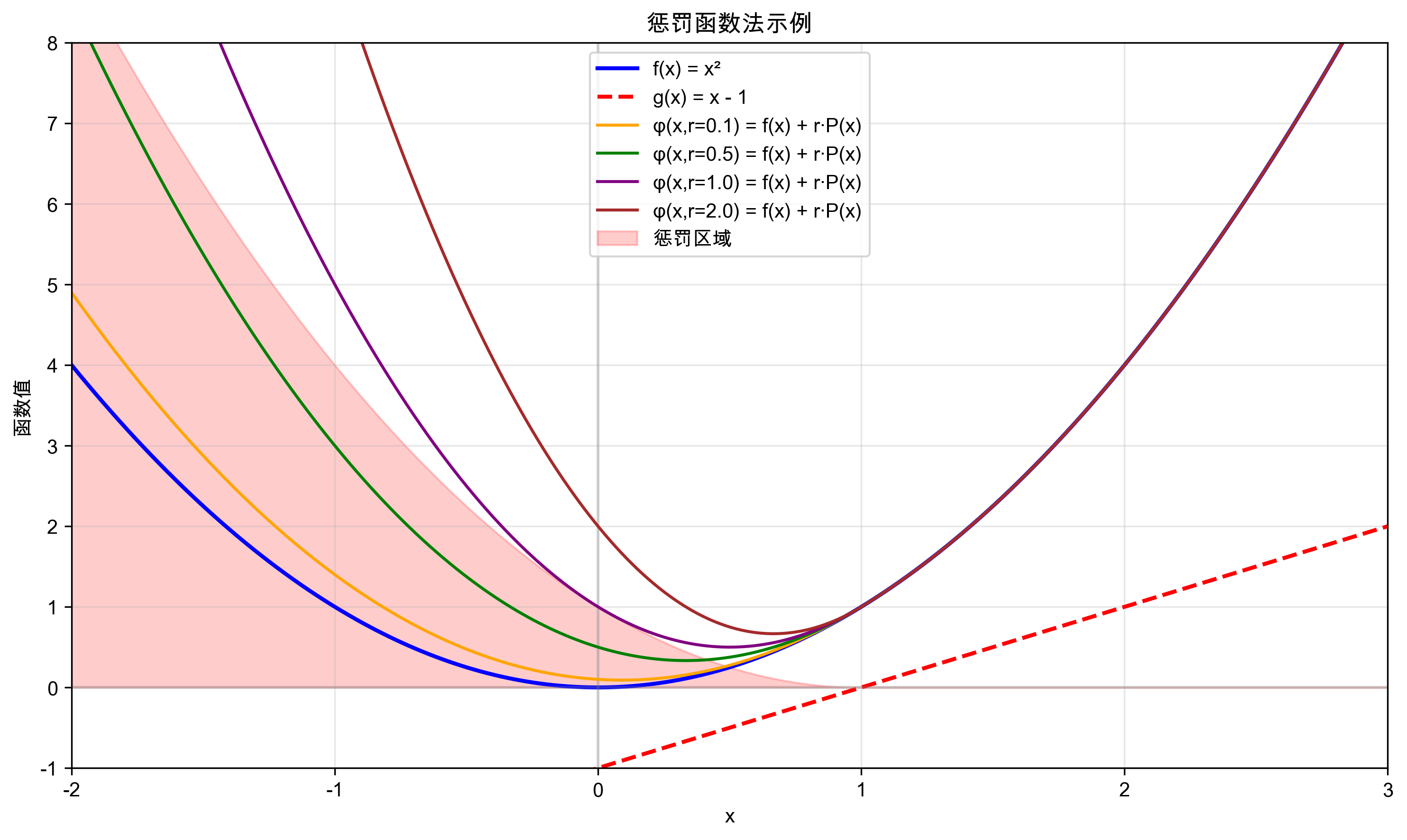
图片说明:
- 左图:展示不同惩罚参数r对惩罚函数形状的影响,随着r增大,最优解逐渐逼近约束边界
- 中图:显示算法收敛过程,迭代解逐渐趋向最优解,惩罚参数按指数增长
- 右图:简单示例,验证惩罚函数法的基本原理
惩罚函数为:
\[\phi(\boldsymbol{x}, r^{(k)}) = f(\boldsymbol{x}) + r^{(k)} \sum_{i=1}^{p} \left\{ \max\big[0,\, g_i(\boldsymbol{x})\big] \right\}^2\]其中,$r^{(k)}$ 为趋于无穷大的严格递增正数列,$r^{(k)} = C\, r^{(k-1)}$ 且 $C>1$,$\lim_{k\to\infty} r^{(k)} = \infty$。迭代点在可行域内时,惩罚项为 0,惩罚函数等于原函数;迭代点在可行域外时,惩罚项大于 0,大于原函数。因此,由于罚因子严格递增,随着迭代进行,可以迫使惩罚项趋于 0,从而逼近原函数。
三、应用
例题1:简单不等式约束问题
题目: 用惩罚函数外点法求解以下约束优化问题:
\[\begin{cases} \min & f(x) = x^2 \\ \text{s.t.} & g(x) = x - 1 \leq 0 \end{cases}\]解答:
-
构造惩罚函数: $\phi(x, r) = x^2 + r \cdot [\max(0, x-1)]^2$
-
分情况讨论:
情况1: 当 $x \leq 1$ 时(满足约束)
$\phi(x, r) = x^2 + r \cdot 0 = x^2$情况2: 当 $x > 1$ 时(违反约束)
$\phi(x, r) = x^2 + r \cdot (x-1)^2$ -
求无约束极值:
对 $\phi(x, r)$ 关于 $x$ 求导:
$\frac{d\phi}{dx} = 2x + 2r(x-1) = 2x + 2rx - 2r = 2x(1+r) - 2r$令 $\frac{d\phi}{dx} = 0$,得:
$x^* = \frac{r}{1+r}$ -
分析收敛性:
$\lim_{r \to \infty} x^* = \lim_{r \to \infty} \frac{r}{1+r} = 1$因此,当 $r \to \infty$ 时,$x^* \to 1$,即最优解为 $x^* = 1$,$f(x^*) = 1$。
例题2:多约束问题
题目: 用惩罚函数外点法求解:
\[\begin{cases} \min & f(x_1, x_2) = x_1^2 + x_2^2 \\ \text{s.t.} & g_1(x_1, x_2) = x_1 + x_2 - 1 \leq 0 \\ & g_2(x_1, x_2) = -x_1 \leq 0 \\ & g_3(x_1, x_2) = -x_2 \leq 0 \end{cases}\]解答:
-
构造惩罚函数: $\phi(x_1, x_2, r) = x_1^2 + x_2^2 + r \sum_{i=1}^{3} [\max(0, g_i(x_1, x_2))]^2$
-
展开惩罚项:
$\phi(x_1, x_2, r) = x_1^2 + x_2^2 + r[\max(0, x_1+x_2-1)]^2 + r[\max(0, -x_1)]^2 + r[\max(0, -x_2)]^2$ -
在可行域内分析:
当 $x_1 \geq 0, x_2 \geq 0, x_1 + x_2 \leq 1$ 时:
$\phi(x_1, x_2, r) = x_1^2 + x_2^2$求极值:$\frac{\partial \phi}{\partial x_1} = 2x_1 = 0$,$\frac{\partial \phi}{\partial x_2} = 2x_2 = 0$
得:$x_1^* = 0, x_2^* = 0$
-
验证约束:
$g_1(0,0) = -1 \leq 0$ ✓,$g_2(0,0) = 0 \leq 0$ ✓,$g_3(0,0) = 0 \leq 0$ ✓因此最优解为 \((x_1^*, x_2^*) = (0, 0)\),最优值为 \(f^* = 0\)。
例题3:等式约束问题
题目: 用惩罚函数法求解:
\[\begin{cases} \min & f(x_1, x_2) = x_1^2 + x_2^2 \\ \text{s.t.} & h(x_1, x_2) = x_1 + x_2 - 2 = 0 \end{cases}\]解答:
-
构造惩罚函数: $\phi(x_1, x_2, r) = x_1^2 + x_2^2 + r(x_1 + x_2 - 2)^2$
-
求偏导数:
$\frac{\partial \phi}{\partial x_1} = 2x_1 + 2r(x_1 + x_2 - 2) = 0$
$\frac{\partial \phi}{\partial x_2} = 2x_2 + 2r(x_1 + x_2 - 2) = 0$ -
求解方程组:
从两个方程可得:$x_1 = x_2$代入第一个方程:
$2x_1 + 2r(2x_1 - 2) = 0$
$2x_1 + 4rx_1 - 4r = 0$
$x_1(2 + 4r) = 4r$
$x_1 = \frac{4r}{2 + 4r} = \frac{2r}{1 + 2r}$ -
求极限:
$\lim_{r \to \infty} x_1 = \lim_{r \to \infty} \frac{2r}{1 + 2r} = 1$因此 $x_1^* = x_2^* = 1$,满足约束 $x_1 + x_2 = 2$,最优值为 $f^* = 2$。
例题4:等式约束问题(博客园例题)
题目: 用外点法求等式约束问题
\[\begin{cases} \min & \frac{1}{2}x_1^2 + \frac{1}{6}x_2^2 \\ \text{s.t.} & x_1 + x_2 = 1 \end{cases}\]解答:
-
构造惩罚函数: $F(x, M_k) = \frac{1}{2}x_1^2 + \frac{1}{6}x_2^2 + M_k(x_1 + x_2 - 1)^2$
-
求偏导数:
$\frac{\partial F}{\partial x_1} = x_1 + 2M_k(x_1 + x_2 - 1) = 0$
$\frac{\partial F}{\partial x_2} = \frac{1}{3}x_2 + 2M_k(x_1 + x_2 - 1) = 0$ -
联立求解:
从两个偏导方程可得:$x_2 = 3x_1$代入第一个方程:
$x_1 + 2M_k(4x_1 - 1) = 0$
$x_1 = \frac{2M_k}{1 + 8M_k}$
$x_2 = 3x_1 = \frac{6M_k}{1 + 8M_k}$ -
求极限:
$\lim_{M_k \to \infty} x_1 = \lim_{M_k \to \infty} \frac{2M_k}{1 + 8M_k} = \frac{1}{4}$
$\lim_{M_k \to \infty} x_2 = \lim_{M_k \to \infty} \frac{6M_k}{1 + 8M_k} = \frac{3}{4}$因此最优解为 \((x_1^*, x_2^*) = (\frac{1}{4}, \frac{3}{4})\)。
例题5:多约束不等式问题
题目: 求解非线性规划
\[\begin{cases} \min & f(x_1, x_2) = x_1 + x_2 \\ \text{s.t.} & x_1^2 - x_2 \leq 0 \\ & -x_1 \leq 0 \end{cases}\]解答:
-
构造惩罚函数:
$P(x, M) = x_1 + x_2 + M[\max(0, x_1^2 - x_2)]^2 + M[\max(0, -x_1)]^2$ -
求偏导数:
\(\frac{\partial P}{\partial x_1} = 1 + 2M[\max(0, x_1^2 - x_2)](2x_1) - 2M[\max(0, -x_1)] = 0\) \(\frac{\partial P}{\partial x_2} = 1 - 2M[\max(0, x_1^2 - x_2)] = 0\) -
分析可行域外的点:
对于 $x_1 < 0, x_2 < 0$ 的情况: \(\begin{cases} 1 + 2M(x_1^2 - x_2)(2x_1) + 2Mx_1 = 0 \\ 1 - 2M(x_1^2 - x_2) = 0 \end{cases}\) -
求解驻点:
解得: \(\begin{cases} x_1 = -\frac{1}{2(1+M)} \\ x_2 = \frac{1}{4(1+M)^2} - \frac{1}{2M} \end{cases}\) -
求极限:
当 $M \to +\infty$ 时: $x_1 \to 0$,$x_2 \to 0$验证:$(0, 0)$ 是可行点,满足所有约束条件,因此是最优解。
例题6:复杂约束问题
题目: 用惩罚函数法解如下非线性规划问题
\[\begin{cases} \min & f(x_1, x_2) = 2x_1 + 2x_2 + 2 \\ \text{s.t.} & -x_1 + x_2^2 \leq 1 \\ & x_2 \geq 5 \end{cases}\]解答:
-
改写为标准形式:
\(\begin{cases} \min & f(x_1, x_2) = 2x_1 + 2x_2 + 2 \\ \text{s.t.} & g_1(x) = -x_1 + x_2^2 - 1 \leq 0 \\ & g_2(x) = -x_2 + 5 \leq 0 \end{cases}\) -
构造惩罚函数:
$\phi(x_1, x_2, r) = 2x_1 + 2x_2 + 2 + r[\max(0, -x_1 + x_2^2 - 1)]^2 + r[\max(0, -x_2 + 5)]^2$ - 分析约束:
- 约束1:$-x_1 + x_2^2 \leq 1$,即 $x_1 \geq x_2^2 - 1$
- 约束2:$x_2 \geq 5$
- 求解思路:
由于 $x_2 \geq 5$,在约束1中 $x_1 \geq 25 - 1 = 24$
目标函数在可行域内单调递增,因此最优解在边界上。
四、参数选择与算法步骤
参数选择
初始点 $x^{(0)}$: 可行域及非可行域内均可。
初始罚因子 $r^{(0)}$: 选择对算法的成败和计算效率有显著影响。
- 选取过小:无约束求解的次数增多,收敛速度慢
- 选取过大:非可行域内惩罚函数比原函数大得多,在起作用约束边界处产生尖点,函数形态变坏,从而限制了某些无约束优化方法的使用,导致计算失败
罚因子递增系数 $C$: 一般取 $C \in [5, 10]$
算法步骤
惩罚函数外点法的详细步骤:
-
在 $n$ 维空间任取初始点 $x^{(0)}$
-
选取初始罚因子 $r^{(0)}$,递增系数 $C$,并置 $k = 0$
-
求解无约束优化问题 $\min \phi(x, r^{(k)})$,得到最优点 $x_k^*$
-
当 $k = 0$ 时转步骤5,否则转步骤6
-
置 $k = k + 1$,$r^{(k+1)} = Cr^{(k)}$,$x_{k+1}^{(0)} = x_k^*$
-
由终止准则,若满足则结束算法,输出最优解;否则转步骤5
五、算法步骤总结
惩罚函数外点法的一般步骤:
-
初始化: 选择初始点 $\boldsymbol{x}^{(0)}$,初始惩罚参数 $r^{(0)} > 0$,放大因子 $C > 1$,精度要求 $\varepsilon > 0$,置 $k = 0$。
-
构造惩罚函数:
$\phi(\boldsymbol{x}, r^{(k)}) = f(\boldsymbol{x}) + r^{(k)} \sum_{i=1}^{p} [\max(0, g_i(\boldsymbol{x}))]^2 + r^{(k)} \sum_{j=1}^{q} [h_j(\boldsymbol{x})]^2$ -
求解无约束优化问题:
$\boldsymbol{x}^{(k+1)} = \arg\min_{\boldsymbol{x}} \phi(\boldsymbol{x}, r^{(k)})$ -
检验收敛性: 若满足收敛准则,停止;否则转步骤5。
-
更新惩罚参数: $r^{(k+1)} = C \cdot r^{(k)}$,置 $k = k+1$,转步骤2。
收敛准则:
- $|\boldsymbol{x}^{(k+1)} - \boldsymbol{x}^{(k)}| < \varepsilon$
- 或惩罚项足够小:$r^{(k)} \sum_{i=1}^{p} [\max(0, g_i(\boldsymbol{x}^{(k+1)}))]^2 < \varepsilon$
算法特点:
- 外点法不保证搜索点保持在可行域内(搜索范围包括可行域和不可行域)
- 适用于包含不等式约束或等式约束的优化问题
- 对目标函数的凹凸性没有要求
- 结合启发式算法(如遗传算法、蚁群算法、禁忌搜索等)几乎可以求解任何问题
- 启发式算法无需目标函数的梯度等信息
注意事项:
- 惩罚函数对目标函数的凹凸性没有要求
- 结合启发式算法几乎可以求解任何问题
- 外点法不保证搜索点保持在可行域内
- 适用于包含不等式约束或等式约束的优化问题